堆排序，优先队列，排序基础

堆排序虽然在性能效率上不及快速排序，但由于优先队列的使用十分广泛，所以堆排序依然是基础中比较重要的部分。

堆的实质其实是一个数组，不过其逻辑结构则是以一颗近似完全二叉树的形式存在的，如图

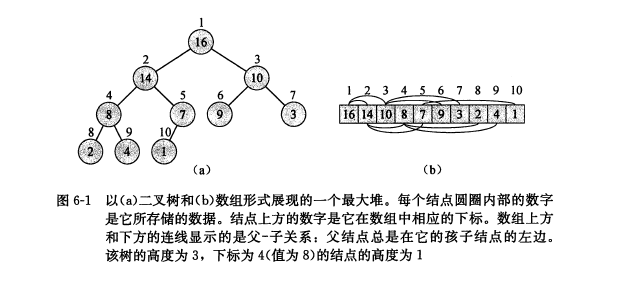
堆（最大堆）的性质：

1.父结点一定大于子节点（最小堆相反）

2.以每个子结点为根结点的树也是堆

由于近似完全二叉树的性质，还可得出如下性质（数组下标以1开头）：

1.叶子结点的数组下标为（(n/2+1)到n）

2.一个结点的左子结点点的下标为2i，右子结点的下标为2i+1

一.  堆性质维护（即堆在改变的情况，性质不变）：

一般人往往会陷入误区，因为人思维的影响往往会一直思考如何建立一个堆，而不是首先思考如何维护一个堆。但是细想会明白建堆的过程就是在不断地改变堆，所以必要先知道如何去维护堆的性质。

思考：根据上述堆的性质，每个结点必须要大于其子结点，如果不大于怎么办？当然是让小的下去，大的上来，现在用伪代码模拟以i结点为子节点的堆维护过程。

伪代码：

PROTECT(A,i)

1.L=i的左子节点下标，R=i右子节点下标，max = i；

2.if（L<=size&&A[L]>A[i]）

　　max = L

3.if（R<=size&&A[R]>A[max]）

　　max = R

4.if（max!=i）

　　exchange(max,i)

　　PROTECT(A,max)

想必大家都知道1-3步的原因，而第4步则是源自堆的父节点一定大于子节点的性质，试想如果max=i那么i已经比它的两个子节点要大，自然就比其子节点的子节点要大，所以该堆已经满足性质，无需再下顺。

而若max！=i则i有可能小于其原子节点的子节点（i并非最大），需继续下顺，由于i与max结点值互换，所以此时max代表的才是i，max 需要继续下顺

代码：

//维护堆的性质
// a 表示堆，i表示当前节点下标 , n表示堆数组的实际长度 
void protect(int *a,int i,int n){
    int max = i;
    int l = i*2;
    int r = i*2+1;
    if(l<=n&&a[l]>a[i]){
        max=l;
    }
    if(r<=n&&a[r]>a[max]){
        max=r;
    }
    if(max!=i){
        int temp;
        temp=a[max];a[max]=a[i];a[i]=temp;
        protect(a,max,n);
    }
}

二.  建堆：

既然维护堆性质的方案已经得出，那么建堆其实就是从以最后一个非叶子节点（n/2）为根节点开始维护堆的性质，一直维护到根节点

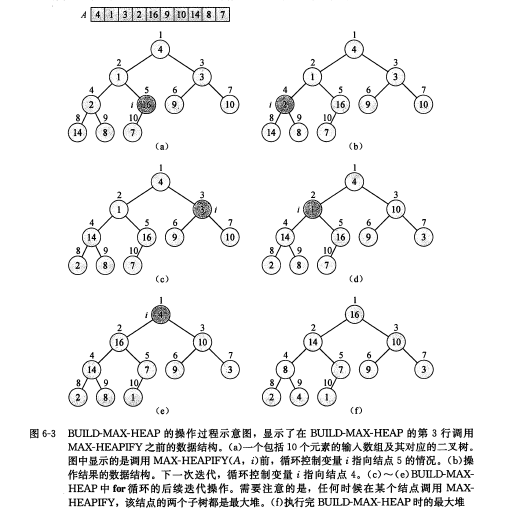
代码：

//建堆
void build(int *a,int n){
    for(int i=n/2;i>=1;i--){
        protect(a,i,n);
    }
}

 三.  堆排序：

思考：经过对堆性质的了解，堆排序无非就是将堆的根节点（最大值）取出放在末端，然后维护堆性质，不断循环直到堆中无结点

整体流程：

1.将顶部结点与数组末端进行互换，并取出（为了将大值放到数组后面）

2.维护堆的性质

3.循环至无结点

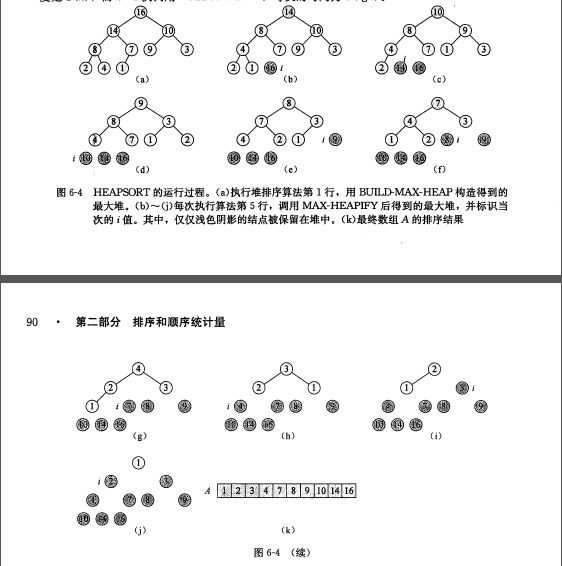
代码：

//堆排序 
void sort(int *a,int n){
    for(int i=N;i>=2;i--){
        int temp=a[i];
        a[i]=a[1];
        a[1]=temp;
        n--;
        protect(a,1,n);
    }
}

整体示例代码：

/*
堆的建立，维护，插入，取出 
*/
#include<iostream>
using namespace std;
#define N 10

//维护堆的性质
// a 表示堆，i表示当前节点下标 , n表示堆数组的实际长度 
void protect(int *a,int i,int n){
    int max = i;
    int l = i*2;
    int r = i*2+1;
    if(l<=n&&a[l]>a[i]){
        max=l;
    }
    if(r<=n&&a[r]>a[max]){
        max=r;
    }
    if(max!=i){
        int temp;
        temp=a[max];a[max]=a[i];a[i]=temp;
        protect(a,max,n);
    }
}

//建堆
void build(int *a,int n){
    for(int i=n/2;i>=1;i--){
        protect(a,i,n);
    }
}

//取出堆顶
int getTop(int *a,int &n){
    int result = a[1];
    a[1]=a[n];a[n]=0;n--;
    protect(a,1,n);
    return result; 
}

//堆排序 
void sort(int *a,int n){
    build(a,n);
    for(int i=N;i>=2;i--){
        int temp=a[i];
        a[i]=a[1];
        a[1]=temp;
        n--;
        protect(a,1,n);
    }
}

int main(){
    int a[N+1];
    for(int i=1;i<=N;i++){
        cin>>a[i];
    }
    int n=10;
    sort(a,n);
    for(int i=1;i<=N;i++){
        cout<<a[i]<<"    ";
    }
    return 0;
} 

 优先队列代码：

/*
优先队列 
*/
#include<iostream>
using namespace std;

//维护优先队列性质 
void protect(int *a,int i,int n){
    int left = 2*i;
    int right = 2*i+1;
    int max = i;
    if(a[left]>a[i]&&left<=n){
        max = left;
    }
    if(a[right]>a[max]&&right<=n){
        max = right;
    }
    if(i!=max){
        int temp = a[max];
        a[max] = a[i];
        a[i] = temp;
        protect(a,max,n); 
    }
}

//建立优先队列
void build(int *a,int n){
    for(int i=n/2;i>=1;i--){
        protect(a,i,n);
    }
}

//取出优先队列头结点
int getTop(int *a,int &n){
    int top = a[1];
    a[1]=a[n];
    n--;
    protect(a,1,n);
    return top;
}

//替换优先列表中的结点 
void replace(int *a,int i,int k){
    if(a[i]>k){
        throw "replace k < node";
    }
    a[i]=k;
    while(i>1&&a[i/2]<a[i]){
        int temp = a[i];
        a[i] = a[i/2];
        a[i/2] = temp;
        i=i/2;
    }
}

void insert(int *a,int k,int &n){
    n++;
    a[n] = 0;
    replace(a,n,k);
}

void sort(int *a,int n){
    build(a,n);
    for(int i=n;i>=1;i--){
        int temp = a[i];
        a[i] = a[1];
        a[1] = temp;
        n--;
        protect(a,1,n);
    }
}

int main(){
    int a[100];
    int n = 10;
    cout<<"输入该数组的10个值：";
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    sort(a,n);
    cout<<"堆排序后：";
    for(int i=1;i<=n;i++){
        cout<<a[i]<<" ";
    }
    cout<<"是否要进行插入：1.是，2.否";
    int select;
    cin>>select;
    if(select == 1){
        int num;
        cout<<"输入要插入的值：";
        cin>>num;
        insert(a,num,n);
        sort(a,n);
        for(int i=1;i<=n;i++){
            cout<<a[i]<<" ";
        }
    }
    return 0;
}