问题描述:这个问题源自《算法导论》中基础部分分治策略讲解,即给出一支股票近15天价格表,要求求出买进卖出获得的最大值及买进时刻卖出时刻。
可百度面试问的没那么简单,要求求出最大收益及次大收益(包括买进卖出时刻),且手上最多只能有一支股票即求出的最大子数组、次大子数组不能重合。(当时直接懵逼)(这次只更新求最大子数组的问题解法)
思考:这是一个非常明确的最大子数组问题(为什么?靠自己对问题描述的敏感度,即多练习),将前后两天相减得出的值放在一个数组里面形成一个正负数掺杂的数组(如果全是正数或负数,那这问题将没有可研究性,原因显而易见),问题便转化为求出这个数组的最大子数组了。
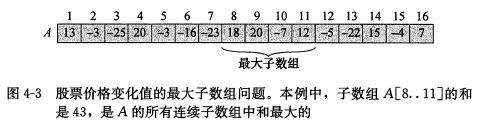
分析:分治策略在于将一个问题分成若干个小问题,问题本身不变只是规模更小,本问题中可将该数组分成左右两半,那么最大子数组要么在左部,要么在右部,要么在跨越左部和右部的中间部分,三种情况,左右两部分也可如此分开,直到分到无法再分,那么其实最后问题就为求跨越重点的最大子数组、左边最大子数组、右边最大子数组中的最大值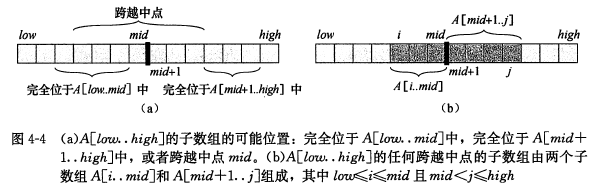
求跨越中点最大子数组方法:(跨越中点即为求i-middle-j的最大子数组,i>=low,j<=high)
int mLeftSum = 0,mRightSum = 0;//中间数组左右两边的最大子数组的和 for(int i = middle;i >= low;i--){ leftTemp = leftTemp + a[i]; if(leftTemp > mLeftSum){ mLeftSum = leftTemp; } }
for(int j = middle + 1;j <= high;j++){ rightTemp = rightTemp + a[j]; if(rightTemp > mRightSum){ mRightSum = rightTemp; } }
return mLeftSum+mRightSum;
那么整体代码:
#include<iostream> #include<string> using namespace std; struct Array{ int sum; int low; int high; }; Array getMax(Array a, Array b, Array c){ Array max = a; if(max.sum<b.sum){ max = b; } if(max.sum<c.sum){ max = c; } return max; } Array getSum(int a[], int low, int high){ if(low == high){ Array result; result.sum = a[low]; result.low = low; result.high = low; return result; } Array left,right,middleArray;//设置三个集合,放置对应的最大子数组和,数组下标 int mLeftSum = 0,mRightSum = 0;//中间数组左右两边的最大子数组的和 //求中间数组两边的最大子数组和 int middle = (low + high) / 2; int leftTemp = 0,rightTemp = 0; int lowTemp,highTemp; left = getSum(a, low, middle); right = getSum(a, middle+1, high); for(int i = middle;i >= low;i--){ leftTemp = leftTemp + a[i]; if(leftTemp > mLeftSum){ mLeftSum = leftTemp; lowTemp = i; } } for(int j = middle + 1;j <= high;j++){ rightTemp = rightTemp + a[j]; if(rightTemp > mRightSum){ mRightSum = rightTemp; highTemp = j; } } middleArray.sum = mLeftSum+mRightSum; middleArray.low = lowTemp; middleArray.high = highTemp; return getMax(left, right, middleArray); } int main(){ int a[100]; int n; cin>>n; for(int i=0;i<n;i++){ cin>>a[i]; } Array result = getSum(a,0,n-1); cout<<"最大子数组和为:"<<result.sum<<", 下标为:"<<result.low<<" 到 "<<result.high; return 0; }