题目背景emmm
[ ext{首先特判掉p=q时的情况(ans = }p^2-1 ext{)}
]
[ ext{构造函数}f(k) = leftlfloor frac{kq}{p}
ight
floor
]
[ ext{考虑这个函数}g(x)=leftlfloor x
ight
floor ext{的几何意义}
]
[ ext{他表示在平面直角坐标系中,横坐标为定值,纵坐标小于等于x的整点个数}
]
[ ext{好,那么我们继续来看f(k),他表示所有横坐标为定值,纵坐标小于等于}frac{kp}{q} ext{的数的个数}
]
[ ext{那么构造}t(k)=frac{kq}{p} ext{,那么}sum_{i=1}^{frac{p-1}{2}}f(k) ext{的几何意义是:}
]
[ ext{所有横坐标}in(1,frac{p-1}{2}); ext{的整数,纵坐标是整数的点数}
]
即
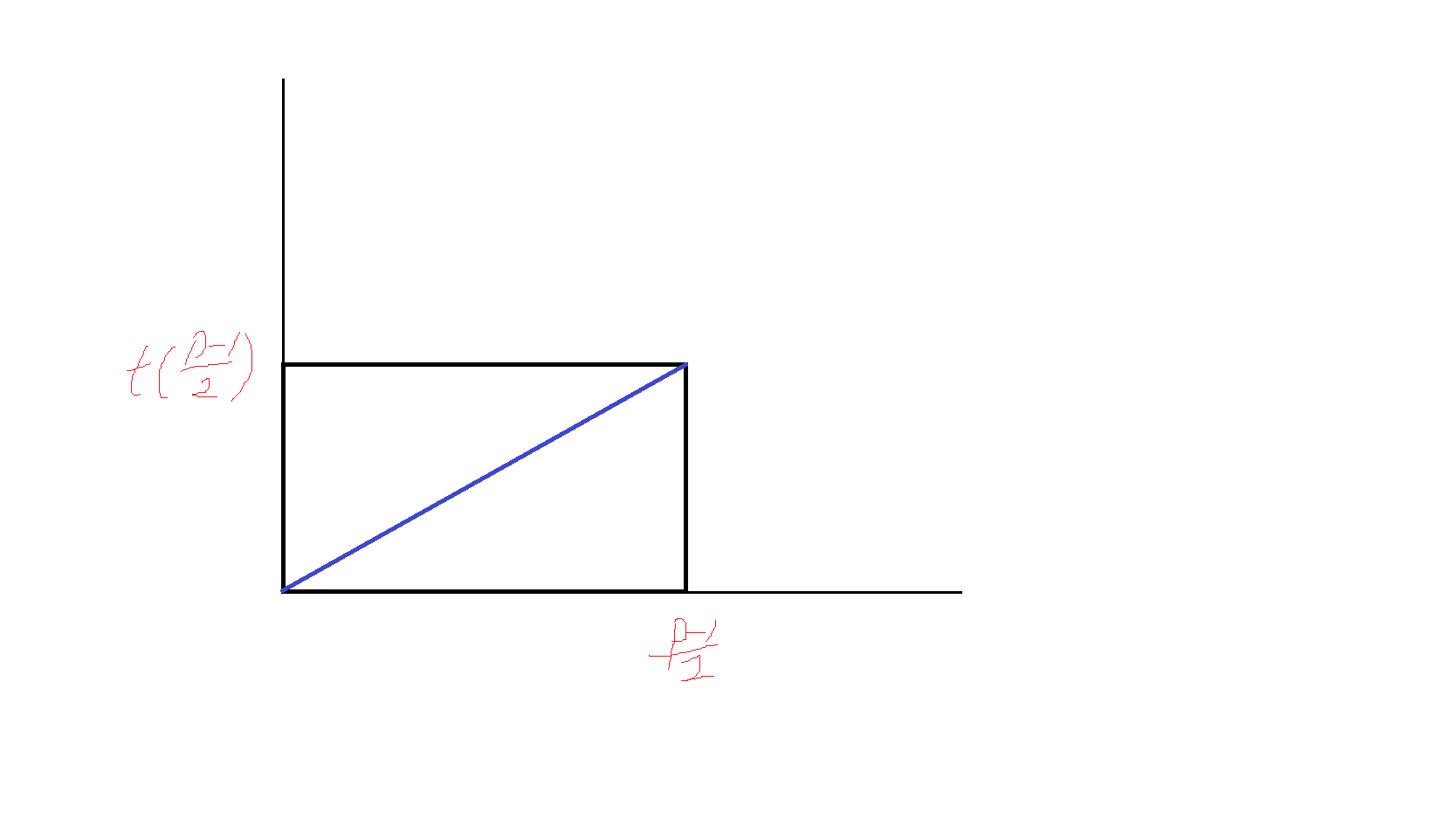
中蓝线以下部分中整点数
~
[ ext{又因为}leftlfloor t(k)
ight
floor_{max} = frac{q-1}{2}
]
[ ext{所有只用考虑纵坐标在直线}{(0,0),(frac{p-1}{2},frac{q-1}{2})} ext{以下的整点}
]
[ ext{然后p,q互换同理}
]
[ ext{所以就是长方形ABCD}(A(0,0),B(0,frac{p-1}{2}),C(frac{q-1}{2},frac{p-1}{2}),D(frac{q-1}{2},0) ext{中整点个数}
]
[ ext{所以答案就是}frac{(p-1) imes(q-1)}{4}
]
然后你就切了这道蓝题~