状压DP
描述状态的维数,维度
首先找题目中在10~20范围内的参数(如果有这样的范围,那么这题就hin可能是状压),它很有可能是一个。
再看题目中的限制条件,它可能也要加进去
难点
状态转移 : 用二进制(或三进制或更⑥的)表示状态,用位运算状态的修改
初始化
常见操作
将x第i位变成1: x |= (1<<(i-1))
将x第i位变成0 : x &= (~(1<<(i-1)))
取出x第i位: (1<<(i-1))&x
取出x最靠右的1: lowbit(x) = x&(-x)
取出x最靠右的0:xx = (~x & 位数), 取xx的lowbit
依次取出一个数的所有的 1 : 取一个lowbit, 减一个lowbit
依次取出一个数的所有的 0 : 同理,取一个0,减一个0(对xx操作
枚举非空子集: for(int x = sta ; x ; x = ((x-1) & sta) )
栗提(我没有状压基础,所以觉得题都挺好的
[SCOI2005]互不侵犯
https://www.luogu.org/problem/P1896
这种求合法的方案的题目,一般需要对与当前状态相契合的合法方案数求和。
首先这题肯定是压N, 然后有国王数这个限制,而且前一行的状态也是个限制,之后综合起来,考虑状态的转移,注意怎么初始化和统计答案。
#include<cstdio>
using namespace std;
const int MAXN = 20;
#define ll long long
int n, KK;
//f[i][s][k]表示前i行(包括第i行),第i行的状态为s,已选k个国王的方案
//f[i][s][k] = Σf[i-1][s'][k - k_num[s]] ,即上一行与当前行相契合的方案都要加进去
ll f[20][1024][40];
int MAX, cnt, can[100], k_num[100];
int main() {
scanf("%d%d",&n, &KK);
int MAX = (1<<n)-1;
int sum;
int tmp;
for(int i = 0; i <= MAX; ++i) {//预处理每一行的合法方案和它对应的国王个数 //预处理要全面!!从0开始
if(i&(i<<1)) continue;//把同行不合法的去掉
can[++cnt] = i;
sum = 0;
tmp = i;
while(tmp) sum += (tmp&1), tmp = tmp>>1;
k_num[cnt] = sum;
}
for(int j = 1; j <= cnt; j++) f[1][j][k_num[j]] = 1;//初始化?
for(int i = 2; i <= n; i++) {//枚举i,s,s'(这里的j),求和
for(int s = 1; s <= cnt; s++) {
for(int j = 1; j <= cnt; j++) {
if((can[s]&can[j]) || ((can[s]<<1)&can[j]) || ((can[s]>>1)&can[j])) continue;//判断是否和前一行冲突(考虑国王的影响范围后易得)
for(int k = k_num[s]; k <= KK; k++) f[i][s][k] += f[i-1][j][k - k_num[s]];//枚举k
}
}
}
long long ans = 0;
for(int j = 1; j <= cnt; j++) ans += f[n][j][KK];//统计答案
printf("%lld",ans);
return 0;
}
JDOJ 1009 五子棋
https://neooj.com:8082/oldoj/problem.php?id=1099
题目大意
有N个人在进行五子棋比赛,每个人都有一 个初始经验值st_exp_i。若i,j比赛一场,i会获 得exp_i,j的经验值,j会获得exp_j,i的经验值, 当前经验值高的人获胜,获胜者会得到sco_i,j 的分数,现在1号队员可以安排比赛顺序,他 希望自己得分最高,请问他最高可以得多少 分。数据范围 : 1<=N<=13
首先一个贪心,只需要求1号的最高得分,所以我们只需要考虑1号和剩下n-1个人的比赛,并且还要先考虑,因为他们在变秃 强。这样我们就可以只压一维的N了。
因为经验与顺序无关,所以可以根据状态直接算出1号的经验,所以不用再开一维,当状态不好表示时,试着增加维度。(即与顺序有关那就hin难了)
#include<cstdio>
#include<string.h>
#include<algorithm>
using namespace std;
const int MAXN = 14;
int n, T;
int st_exp[MAXN], exp[MAXN][MAXN], sco[MAXN][MAXN];
int f[1<<MAXN];
int MAX;
void init() {
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++) scanf("%d",&exp[i][j]);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++) scanf("%d",&sco[i][j]);
for(int i = 1; i <= n; i++) scanf("%d",&st_exp[i]);
}
int getexp(int s) {
int exp1 = st_exp[1];
for(int i = 1; i <= n; i++) if(s&(1<<(i-1))) exp1 += exp[1][i+1];
return exp1;
}
int main() {
scanf("%d",&T);
while(T--) {
memset(f, 0, sizeof(f));
scanf("%d",&n);
init();
n--;
//考虑安排先把前n-1个人安排着和1号vs
MAX = (1<<n)-1;
int exp1;//根据状态直接算出1号的经验
for(int s = 0; s <= MAX; s++) {
exp1 = getexp(s);
for(int j = 1; j <= n; j++) {
if(s&(1<<(j-1))) continue;
if(exp1 > st_exp[j+1]) f[s|(1<<(j-1))] = max(f[s|(1<<(j-1))], f[s] + sco[1][j+1]);
else f[s|(1<<(j-1))] = max(f[s|(1<<(j-1))], f[s]);
}
}
printf("%d
",f[(1<<n)-1]);
}
return 0;
}
[USACO06NOV]玉米田Corn Fields
https://www.luogu.org/problem/P1879
和上面的互不侵犯一样
#include<cstdio>
#include<algorithm>
using namespace std;
const int mod = 100000000;
int n,m, ans;
int f[13][1000];//f[i][j]: 第i行选用状态can[i].st[j]这个状态时,方案数
struct node{
int num;
int st[5000];
}can[13];//can[i]:第i行所有合法的状态,及状态数
void getstate(int hi, int t) {
int num = 0;
for(int i = 0; i < (1<<m); i++) {//i==0 ->可以不种草
if((i&(i<<1)) || (i&(i>>1)) || (t&i)) continue;//t&i==1 -> 非法种草
can[hi].st[++num] = i;
}
can[hi].num = num;
}
void init() {//初始化每一行合法方案
int t, x;
for(int i = 1; i <= n; i++) {
t = 0;
for(int j = 1; j <= m; j++) {
scanf("%d",&x);
t = (t<<1)+1-x;//把这一行的状态弄成十进制,注:1表示不能种草(这样方便判断种草的位置是否合法)
}
getstate(i, t);
}
}
int main() {
scanf("%d%d",&n,&m);
init();
for(int j = 1; j <= can[1].num; j++) f[1][j] = 1;//初始化第一行
for(int i = 1; i < n; i++)
for(int j = 1; j <= can[i].num; j++)
for(int k = 1; k <= can[i+1].num; k++) {//刷表法
if(can[i+1].st[k] & can[i].st[j]) continue;
else f[i+1][k] += f[i][j];
}
// for(int i = 2; i <= n; i++)
// for(int j = 1; j <= can[i].num; j++) {
// f[i][j] = 0;//填表法比上面的多个初始化
// for(int k = 1; k <= can[i-1].num; k++) {
// if(can[i].st[j]&can[i-1].st[k]) continue;
// else f[i][j] += f[i-1][k];
// }
// }
for(int j = 1; j <= can[n].num; j++) ans = (ans+f[n][j]) %mod;
printf("%d
",ans);
return 0;
}
这里要注意的一个细节:
我们在做这种有的位置是障碍的题目(如上题的坏田,如下题的高地)时,我们可以把障碍处填1,可以放东西的地方填0,这样,我们一个&就可以判断当前的位置是否可以放东西,进而求出每行合法的状态。要注意操作是<<左移,想想我们判断的数 的二进制。
[NOI2001]炮兵阵地
https://www.luogu.org/problem/P2704
题目大意
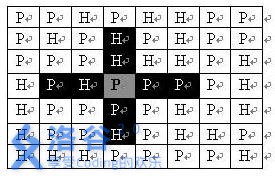
给出一张n*m的地图,其中有一些是平原,一些是高地,现在有一些炮兵要在这块地图上进行部署,炮兵无法部署在高地上,同时他们不能够互相攻击
问地图上最多能部署多少炮兵部队。
右图黑块为灰块可
数据范围
N≤100,M≤10
错误代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<string.h>
using namespace std;
int n,m,debug;
int f[3][60][60];//f[i][st1][st2]:当前为第i行,第i行状态为st[st1], 第i-1行状态为st[st2]时的最大方案数
//影响答案的只有三行
struct node{
int num, st[60];
int num_s[60];//状态st[i]所拥有的士兵个数为num_s[i]
}can[100+9];
int getone(int x) {
int num = 0;
while(x) x -= x & -x, num++;
return num;
}
void getstate(int hang, int st) {
int num = 0;
for(int i = 0; i < (1<<m); i++) {
if( (i&(i<<1)) || (i&(i<<2)) || (i&(i>>1)) || (i&(i>>2)) || (i&st)) continue;
can[hang].st[++num] = i;
can[hang].num_s[num] = getone(i);
}
can[hang].num = num;
}
void init() {//get每行合法的情况
string s;
int t, tmp;
for(int i = 1; i <= n; i++) {
cin>>s;
t = 0;
for(int j = 0; j < m; j++) {
tmp = s[j]=='H' ? 1 : 0;
t = (t<<1)+tmp;//山地不放
}
// if(debug == 2) printf("第%d行的t值: %d
", i, t);
getstate(i, t);
}
}
void pre() {//初始化一二行
for(int j = 1; j <= can[1].num; j++) f[1][j][0] = can[1].num_s[j];
for(int j = 1; j <= can[2].num; j++)
for(int k = 1; k <= can[1].num; k++) {
if(can[2].st[j]&can[1].st[k]) continue;
f[2][j][k] = can[2].num_s[j] + can[1].num_s[k];
}
}
int main() {
// freopen("02.in", "r", stdin);
// freopen("02.out", "w", stdout);
debug = 1;
scanf("%d%d",&n,&m);
init();
pre();
// if(debug == 1) {
// for(int i = 1; i <= n; i++) {
// printf("第%d行的合法情况如下, 共%d个合法情况
",i, can[i].num);
// for(int j = 1; j <= can[i].num; j++) printf("士兵数:%d ; 状态: %d
", can[i].num_s[j] ,can[i].st[j]);
// }
// }
for(int i = 3; i <= n; i++)
for(int j = 1; j <= can[i].num; j++)
for(int k = 1; k <= can[i-1].num; k++) {//士兵数从上往下只增不减,所以不用初始化f[i][j][k]
if(can[i].st[j]&can[i-1].st[k]) continue;//填表法
for(int up2 = 1; up2 <= can[i-2].num; up2++) {
if(can[i-2].st[up2]&can[i-1].st[k] || can[i-2].st[up2]&can[i].st[j]) continue;
f[i%3][j][k] = max(f[i%3][j][k], f[(i-1)%3][k][up2]+can[i].num_s[j]);
}
}
int ans = 0;
for(int j = 1; j <= can[n].num; j++)
for(int k = 1; k <= can[n-1].num; k++) {
if(can[n].st[j]&can[n-1].st[k]) continue;//???
ans = max(ans, f[n%3][j][k]);
}
printf("%d
",ans);
//为什么只用前一个和当前的:我们只需要这样就可以表示出所有要用的状态了
return 0;
}
例题就到这里哈,有兴趣的可以看看标签哦