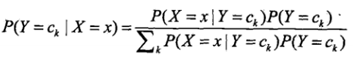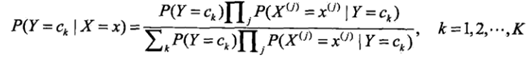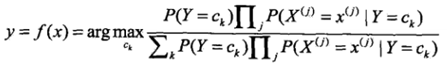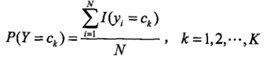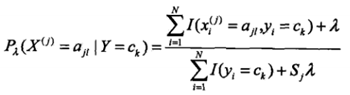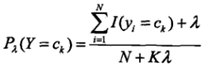朴素贝叶斯是一种很简单的分类方法,之所以称之为朴素,是因为它有着非常强的前提条件-其所有特征都是相互独立的,是一种典型的生成学习算法。所谓生成学习算法,是指由训练数据学习联合概率分布P(X,Y),然后求得后验概率P(X|Y)。具体来说,利用训练数据学习P(X|Y)和p(Y)的估计,得到联合概率分布:
概率估计可以是极大似然估计,或者贝叶斯估计。
假设输入 X 为n维的向量集合,输出 Y 为类别,X 和 Y 都是随机变量。P(X,Y)是X和Y的联合概率分布,训练数据集为:
首先,我们要明确我们求解的目标是:![]() ,即给定某个输入X,我们要判断其所属类别Ck。由概率论知识,我们有:
,即给定某个输入X,我们要判断其所属类别Ck。由概率论知识,我们有:
代入公式得:
这是朴素贝叶斯分类的基本公式。于是,朴素贝叶斯分类器可以表示为
由于,分母对所有的Ck都是相同的,所以
那么如果给定一个输入 X,我们只需要找到一个类别Ck,使得![]() 最大。那么Ck,就是 X 的最佳类别了。
最大。那么Ck,就是 X 的最佳类别了。
下面我们来讲讲朴素贝叶斯法的参数估计,为什么要估计朴素贝叶斯的参数呢,这些参数是什么?首先,我们要明确。现实中,给定我们一批数据,我们就知道其分布,但是具体的数据分布的概率我们是不知道的。也就是说先验概率和条件概率我们是不知道的,这就需要我们来利用其数据的分布估计其先验概率和条件概率了。统计学习中最常用的参数估计就是极大似然估计了,这里我们也可以用贝叶斯估计,其实就是在极大似然估计基础上添加了拉普拉斯平滑(Laplace smoothing)。
由于极大似然估计之前已经讲到过,这里公式我也没有具体来推,所以先验概率和条件概率直接给出来。
先验概率P(Y = Ck)和条件概率的极大似然估计如下:
这样,给定具体的数据,我们就可以估计其先验概率和条件概率,进而计算出后验概率得到所属类别。
同样,贝叶斯估计和极大似然估计差不多,贝叶斯估计只是在极大似然估计上添加了一个拉普拉斯平滑。具体如下:
条件概率的贝叶斯估计如下:
先验概率的贝叶斯估计如下:
下面来给出一个简单的朴素贝叶斯实现代码,代码比较容易理解。只是课本上给出的特征是离散的,而code里面的特征是连续的。原理上其实是一样一样的~
1: % NAIVE BAYES CLASSIFIER
2:
3: clear
4: tic
5: disp('--- start ---')
6:
7: distr='normal';
8: distr='kernel';
9:
10: % read data
11: White_Wine = dataset('xlsfile', 'White_Wine.xlsx');
12: X = double(White_Wine(:,1:11));
13: Y = double(White_Wine(:,12));
14:
15: % Create a cvpartition object that defined the folds
16: c = cvpartition(Y,'holdout',.2);
17:
18: % Create a training set
19: x = X(training(c,1),:);
20: y = Y(training(c,1));
21: % test set
22: u=X(test(c,1),:);
23: v=Y(test(c,1),:);
24:
25: yu=unique(y);
26: nc=length(yu); % number of classes
27: ni=size(x,2); % independent variables
28: ns=length(v); % test set
29:
30: % compute class probability
31: for i=1:nc
32: fy(i)=sum(double(y==yu(i)))/length(y);
33: end
34:
35: switch distr
36:
37: case 'normal'
38:
39: % normal distribution
40: % parameters from training set
41: for i=1:nc
42: xi=x((y==yu(i)),:);
43: mu(i,:)=mean(xi,1);
44: sigma(i,:)=std(xi,1);
45: end
46: % probability for test set
47: for j=1:ns
48: fu=normcdf(ones(nc,1)*u(j,:),mu,sigma);
49: P(j,:)=fy.*prod(fu,2)';
50: end
51:
52: case 'kernel'
53:
54: % kernel distribution
55: % probability of test set estimated from training set
56: for i=1:nc
57: for k=1:ni
58: xi=x(y==yu(i),k);%the feature of dimension-k with respect to label yu(i)
59: ui=u(:,k);
60: fuStruct(i,k).f=ksdensity(xi,ui);
61: end
62: end
63: % re-structure
64: for i=1:ns
65: for j=1:nc
66: for k=1:ni
67: fu(j,k)=fuStruct(j,k).f(i);
68: end
69: end
70: P(i,:)=fy.*prod(fu,2)';
71: end
72:
73: otherwise
74:
75: disp('invalid distribution stated')
76: return
77:
78: end
79:
80: % get predicted output for test set
81: [pv0,id]=max(P,[],2);
82: for i=1:length(id)
83: pv(i,1)=yu(id(i));
84: end
85:
86: % compare predicted output with actual output from test data
87: confMat=myconfusionmat(v,pv);
88: disp('confusion matrix:')
89: disp(confMat)
90: conf=sum(pv==v)/length(pv);
91: disp(['accuracy = ',num2str(conf*100),'%'])
92:
93: toc
1: function confMat=myconfusionmat(v,pv)
2:
3: yu=unique(v);
4: confMat=zeros(length(yu));
5: for i=1:length(yu)
6: for j=1:length(yu)
7: confMat(i,j)=sum(v==yu(i) & pv==yu(j));
8: end
9: end
如果想要实验数据的话,请在博客下面评论区域注明,我看到了会第一时间上传。