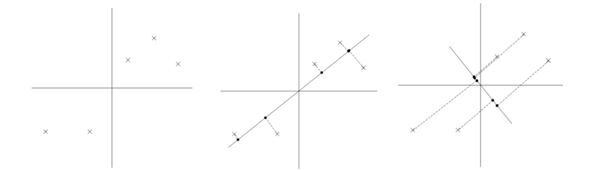
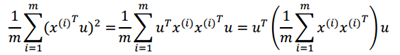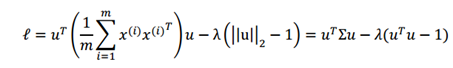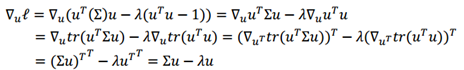其实之前写过PCA相关的博文，但是由于之前掌握的理论知识有限，所以理解也比较浅。这篇博文，我们以另外一种角度来理解PCA看，这里我假设大家对PCA都有一个初步的了解。首先，我们举一个二维空间中的例子，如下图：
左图表示二维空间中的五个点，我们试图找一个投影方向使得这5个点投影在这个方向上的方差最大。这里举了两个例子中图和右图，很明显中图的方差是所有投影方向中方差最大的投影方向。ps：这里解释一下方差的意义，纯属个人理解。设想一下，如果我们有一个投影方向A 和 B, 原始特征经过A 投影后数据几乎集中在一点，也就是说方差几乎为零。这个时候我们可以认为，投影后的样本在这一维上的特征几乎是一样一样的。这样一来我们得到新的空间里特征反映的信息就非常少，我们有理由认为这个投影方向非常差。相反呢，如果经过B 投影后，样本在新的特征空间方差非常大（如中图），我们认为新的样本这一维上的信息非常明确，也就是说这个投影方向是一个“主投影方向”。PCA的目的就是要找到最好的k个“主投影方向”，怎么来判断这个投影方向好不好，我们已经讲了，用方差：投影后方差越大就越好。
接下来我们用数学公式来证明一下：假设我们有m个样本，u是要求解的投影方向，
为样本点，这里的已经去均值化了，那么最大化方差可以形式化最大下面式子：
ps：这里解释一样，
这是方差的计算公式，样本在投影后对应的新的样本是
，由于原始空间去均值化这里新得到的样本也去均值化了，所以新的样本的方差就可以表示为
，后面的式子就不解释了，并且这里
。
于是乎，我们就把最大化方差这个问题转化为求解这个式子
的特征向量的问题了。至于为什么是这样呢，数学上有证明，如下：（这里使用的市拉格朗日方程来求解最大化问题）
对u求导可得：
令导数为零就可以知道u就是
的特征向量了，并且这些特征向量都是正交的，于是我们选取最大k个特征值对应的特征向量就可以构成方差最大的子空间了，样本投影在这个子空间每一维上的方差最大。
总结：博文虽短，但是对于一些对PCA有一定了解却不知所以然的人，相信还是值得一看的。