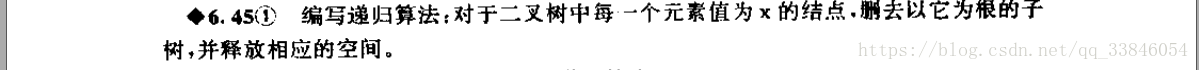数据结构题集(C语言版 清华大学出版社)

数据结构 第六章 树

清华大学出版社数据结构习题集 第六章 树 整理

输入数据
13
1 2 3 0 0 1 0 0 0 0 0 0 1
6

// 35 顺序存储结构
const int MAXSIZE = 20;
typedef struct
{
    Elemtype data[MAXSIZE+1]; // data[0]不存储元素，因为顺序存储结构二叉树的根节点从1开始层次遍历+1
    int length;
}SqBiTree;
void createSqBiTree(SqBiTree &st)
{
    Elemtype x;
    int n;
    cout << "n:";
    cin >> n;
    for  (int i = 0;i<n;i++)
    {
        cin>>x;
        st.data[i+1] = x;
    }
    st.length = n;
}
void print(SqBiTree &st)
{
    for (int i=1;i<=st.length;i++)
        cout << st.data[i]<<' ';
}
// 求出下标志为I的结点对应的十进制整数
// 思路：parent = i/2,如果为偶数则为0，奇数则为1
int thirty_five(SqBiTree &st,int i)
{
    int sum  =0;
    int j = 0;
    while (i)
    {
        if (i%2!=0)
        {
            sum += pow(2,j);
        }
        j++;
        i = i/2;
    }
    return sum;
}
int main()
{
    SqBiTree st ;
    createSqBiTree(st);
    cout << "i:";
    int i;cin>>i;
    cout << "十进制整数："<<thirty_five(st,i)<<endl;
    return 0;
}

// 36 判定两棵二叉树是否相似
int similar(BiTree &t1,BiTree &t2)
{
    if (t1==NULL && t2==NULL)
        return 1;
    if (t1!=NULL && t2!=NULL)
    {
        int l = similar(t1->lchild,t2->lchild);
        int r = similar(t1->rchild,t2->rchild);
        return l&r;
    }else
    return 0;
}
int main()
{
    BiTree t1,t2;
    createBiTree(t1);
    createBiTree(t2);
    if (similar(t1,t2))
        cout <<"similar!"<<endl;
    else
        cout <<"not similar!"<<endl;
    return 0;
}

// 39 增设双亲域和标志域时不用栈进行后序遍历的递推形式
typedef struct NBiNode
{
    Elemtype data;
    struct NBiNode *lchild,*rchild,*parent;
    int mark;// 0 1 2
}NBiNode,*NBiTree;
void createNBiTree(NBiTree &nt,NBiTree &parent)
{
    Elemtype x;
    cin >> x;
    if (x!='#')
    {
        nt = (NBiTree)malloc(sizeof(NBiTree));
        nt->data = x;
        nt->mark = 0;
        nt->parent = parent;
        createNBiTree(nt->lchild,nt);
        createNBiTree(nt->rchild,nt);
    }
    else
    {
        nt = NULL;
    }
}
/*
思路：
1. 从parent走到当前子树根节点，Mark为0，转为1
2. Mark为1时：转到左子树，设Mark为2
3. Mark为2时转到右子树，设Mark为0哦，访问结点
*/
void postOrderUnWithPM(NBiTree &t)
{
    NBiTree p = t;
    while (p){
       switch(p->mark)
    {
    case 0:
        // 第一次访问P结点
        p->mark  =1;
        if (p->lchild)
            p = p->lchild;
        break;
    case 1:
        // 第二次访问P结点
        p->mark = 2;
        if (p->rchild)
            p = p->rchild;
        break;
    case 2:
        // 访问右结点结束后需要打印根节点
        cout << p->data << ' ';
        p->mark = 0;
        p = p-> parent;
        break;
    }
    }

}
int main()
{
    NBiTree nt;
    NBiTree p;
    p =NULL;
    createNBiTree(nt,p);
    postOrderUnWithPM(nt);

    return 0;
}

// 40 只设双亲域不用栈如何中序遍历
typedef struct NBiNode
{
    Elemtype data;
    struct NBiNode *lchild,*rchild,*parent;
}NBiNode,*NBiTree;
void createNBiTree(NBiTree &nt,NBiTree &parent)
{
    Elemtype x;
    cin >> x;
    if (x!='#')
    {
        nt = (NBiTree)malloc(sizeof(NBiTree));
        nt->data = x;
        nt->parent = parent;
        createNBiTree(nt->lchild,nt);
        createNBiTree(nt->rchild,nt);
    }
    else
    {
        nt = NULL;
    }
}


void midOrder(NBiTree &nt)
{
    NBiTree p = nt;
    while (p)
    {
        if (p->lchild)
        {
            p = p->lchild;
        }
        else
        {
            cout << p->data <<' '; // 从左子树回到根节点，打印根节点；此时根据右子树是否为空进行判断
            while (!p->rchild)
            {//右子树为空，两种情况，1. 双亲的左子树：往上走，打印结点；2 双亲的右子树，不必打印
                 while (p->parent && p->parent->rchild == p)
                 {
                     p = p->parent;
                 }
                 if (p->parent)
                 {
                     if (p->parent->lchild == p)
                     {
                         p = p->parent;
                         cout << p->data << ' '; // 走到根节点又要判断右子树是否为空
                     }
                 }else
                 {
                     return ;// 右子树的双亲为空，那就是中序遍历完啦！
                 }
            }
            // 右子树不为空，往右走
            p = p->rchild;

        }
    }
}

int main()
{
    NBiTree nt;
    NBiTree p;
    p =NULL;
    createNBiTree(nt,p);
    midOrder(nt);
    return 0;
}

// 45 
// 递归，对于二叉树中的每一个元素值为X的结点，删去以他为根的子树，并释放相应空间
// 递归清空子树
void delete2(BiTree &t)
{
    if (!t) return ;
    if (t->lchild)
        delete2(t->lchild);
    if (t->rchild)
        delete2(t->rchild);
    delete t;
    t = NULL; // 
}
void deleteBiTree(BiTree &t,Elemtype x)
{
    if (t)
    {
        if (t->data == x ) // string.h 和 string 这真的是两个头文件！
            delete2(t);
        else { // 如果删除了左右孩子就都没有了！★
        deleteBiTree(t->lchild,x);
        deleteBiTree(t->rchild,x);
        }
    }
}

int main()
{
    BiTree t;
    createBiTree(t);
    Elemtype x;
    cout << "x:";
    cin >> x;
    deleteBiTree(t,x);
    preOrder(t);
    return 0;
}

// 48 求两节点的共同祖先
// 找到root到P的路径存到数组中
// 思路：比较根节点和P指针是否相同，若相同返回1已找到；否则压入根节点，判断左右子树能否找到该结点并返回1
// 如果左右子树均没有找到也就意味着该路径上没有P结点（走错路啦！）弹栈出根节点
int findPath(BiTree &root,Elemtype &p,BiTree a[],int &top)
{
    if (root->data == p )
        return 1; // 先比较根节点：相等则返回1，说明找到p,但此时路径数组为空，说明没有祖先
    a[++top] = root; // 根节点入栈
    int has = 0;
    if (root->lchild)
        has = findPath(root->lchild,p,a,top);
    if (has == 0 && root->rchild)
        has = findPath(root->rchild,p,a,top);
    if (has == 0)
    {
        top -- ;
    }
    return has;
}

BiTree findGrandpa(BiTree &root,Elemtype p,Elemtype q)
{
    int top1 = -1,top2 = -1; // TOP 指向a,b的顶层
    // 存储两节点的路径到数组中，寻找相同的最靠右的部分
    BiTree a[20]={};
    BiTree b[20]={};
    if (findPath(root,p,a,top1)!=0 && findPath(root,q,b,top2)!=0)
    {
        for (int i = top1;i>-1;i--)
            for (int j = top2;j>-1;j--)
            if (a[i]== b[j])
                return a[i];
    }
}
int main()
{
    BiTree t;
    createBiTree(t);
    Elemtype p,q;
    cout <<"p,q:";
    cin >> p >> q;
    BiTree grand = findGrandpa(t,p,q);
    cout << "grandpa : " << grand->data <<endl;
    return 0;
}

判断一棵二叉树是否是完全二叉树

我们要如何判断一棵二叉树是否是完全二叉树？？？
1）如果一个结点有右孩子而没有左孩子，那么这棵树一定不是完全二叉树。
2）如果一个结点有左孩子，而没有右孩子，那么按照层序遍历的结果，这个结点之后的所有结点都是叶子结点这棵树才是完全二叉树。
3）如果一个结点是叶子结点，那么按照层序遍历的结果，这个结点之后的所有结点都必须是叶子结点这棵树才是完全二叉树。
求一棵二叉树的层序遍历，我们借助的是数据结构—-队列。如果一个结点不是叶子结点，我们将当前结点出队，将其孩子入队；如果一个结点是叶子结点，我们直接将其出队即可。这是之前求一棵树层序遍历的结果的思路，我们可以借助这个思路，来完成此题。
根据上边分析的2）和3），我们知道，如果一个结点没有左右孩子或者仅有左孩子，它之后的结点必须全部是叶子结点，这棵树才可能是完全二叉树。所以，我们必须定义一个bool变量，来记录是否到了满足2）或者3）的结点，如果满足，我们只需要判断它之后的结点是否是叶子结点即可。

// 49 编写算法判定给定二叉树是否为完全二叉树
/*
1. 层次搜索
2. 设一个布尔数组记录访问过的结点，检查数组中是否有false
3. 递归算法：给出完全二叉树与原定义等价的递归定义，设计一个判别给定的二叉树是满二叉树、不满二叉树还是非完全二叉树的递归函数

*/
const int Maxsize = 20;
// 2. 检查数据中是否有false
bool isFull(BiTree &t)
{
    BiTree  que[Maxsize];
    int front = 0,rear = 0;
    BiTree p;
    Elemtype data[Maxsize] = {};
    int i = 0;
    if (t)
    {
        rear = (rear + 1)%Maxsize;
        que[rear] = t;
        data[i] = t->data;
        while (front != rear)
        {
            front = (front+1)%Maxsize;
            p = que[front];
            if (p->lchild)
            {
                rear = (rear+1)%Maxsize;
                que[rear]=p->lchild;
                data[++i] = p->lchild->data;
            } // 有左子树则放入数据否则放入零
            else
                data[++i] = 0;
            if (p->rchild)
            {
                rear = (rear+1)%Maxsize;
                que[rear]=p->rchild;
                data[++i] = p->rchild->data;
            }
            else
                data[++i] = 0;

        }
        for (int j = 1;j<i;j++)
    { // 检查是否有字母夹着单个0的情况，因为最后也都是0
        if (data[j-1]!=0 && data[j+1]!=0 && data[j] == 0)
            return false;
    }
    }
    return true;
}

// 用一个数组记录遍历过得结点序号，看是否连续
bool isFull2(BiTree &t)
{
    int i=0,j=0;
    BiTree que[Maxsize] = {}; // front
    int order[Maxsize] = {}; // j i
    BiTree p;
    int front = 0,rear = 0;
    if (t)
    {
        que[++rear] = t;
        order[++i] = ++j; // order[1] = 1 根节点序号
        while (front != rear)
        {
            p = que[++front];
            if (order[i]!= order[i-1]+1) // 结点序号不连续
                return false;
            if (p->lchild)
            {
                que[++rear] = p->lchild;
                order[++i] = 2*p->data;
            }
            if (p->rchild)
            {
                que[++rear] = p->rchild;
                order[++i] = 2*p->data+1;
            }
        }
        return 1 ;
    }
}
int main()
{
    BiTree t;
    createBiTree(t);
    cout << isFull2(t)<< endl;
    return 0;
}

// 50
/*
1. 三元组序列 (F, C, L/R)
2. ^代表根节点的双亲
3. ^^代表输入终点
4. 层次表示输入
*/
BiTree three()
{
    Elemtype thr[3];
    BiTree que[Maxsize];
    int front = 0,rear =0;
    BiTree t,p,q;
    cin >> thr[0] >>thr[1] >> thr[2];
    while (thr[0]!='^' || thr[1]!='^')
    {
        if (thr[0] == '^' )
        {
            t = (BiTree )malloc(sizeof(BiTree));
            t->data = thr[1];
            t->lchild = NULL;
            t->rchild = NULL;
            que[++rear] = t; // 根节点入队
            p = t;
            front = 1;
        }
        else
        {
            if (thr[2] == 'L')
            {
                p->lchild = q;
            }
            if (thr[2]=='R')
            {
                p->rchild = q;
            }
        }

        cin >> thr[0] >> thr[1] >> thr[2];
        q = (BiTree)malloc(sizeof(BiTree));
        q->data = thr[1];
        q->lchild  = NULL;
        q->rchild = NULL;
        que[++rear] = q;
        // 每输入一组，便把数据入队
        if (thr[0] != p->data)
        {
            // 出队
            p = que[++front];
        }

    }
    return t;
}
int main()
{
    BiTree t;
    t = three();
    preOrder(t);

    return 0;
}
//51 输出以二叉树表示的算数表达式，如果右括号在输出时应添上
bool isOperator(Elemtype c)
{
    if (c=='+' || c=='-' || c=='*' || c=='/')
        return true;
    else
        return false;
}
bool lowPrior(Elemtype a,Elemtype b)
{
    if ((a == '+' || a == '-')&&(b=='*' || b == '/'))
        return true;
    else
        return false;
}
void biao(BiTree &t)
{
    if (t)
    {
        if (t->lchild)
        {
            if (isOperator(t->lchild->data) && lowPrior(t->lchild->data,t->data))
            {
                // 如果左孩子是操作符并且优先级低于根节点
                cout << '(' << ' ';
                biao(t->lchild);
                cout <<')' << ' ';
            }
            else
                biao(t->lchild);
        }

        cout << t->data << ' ';

        if (t->rchild)
        {
            if (isOperator(t->rchild->data) && lowPrior(t->rchild->data,t->data))
            {
                // 如果左孩子是操作符并且优先级低于根节点
                cout << '(' << ' ';
                biao(t->rchild);
                cout <<')' << ' ';
            }
            else
                biao(t->rchild);
        }
    }
}

int main()
{
    BiTree t;
    createBiTree(t);
    preOrder(t);
    // biao(t);

    return 0;
}
// 52 一棵二叉树的繁茂度定义为各层节点数的最大值与树的高度的乘积

int fanmao(BiTree &t)
{
    int level,v,i,j;
    float f;
    int maxrow,maxcol ; // 最大行和最大列
    BiTree que[Maxsize] =  {}; // 队列
    int order[Maxsize] = {};// 存放各节点序号
    int count[Maxsize] ={};//下标代表层，数组内容为各层结点个数
    v = 0;i = 0;j = 0;maxcol = 0;maxrow = 0;
    if (t)
    {
        que[j] = t;
        order[j] = 1;
        j ++ ;
        while (i<j)
        {
            f = log(order[i])/log(2) ;
        // 将 x 的自然对数值除以 n 的自然对数值，就可以对任意底 n 来计算数值 x 的对数值：Logn(x) = Log(x) / Log(n)
            level = (int)f +1 ;// 当前i节点的层数
            if (maxrow < level)
                maxrow = level;
            count[level] ++;
            // 求出每个节点当前层数，使当前层数的数据++
            if (maxcol <count[level])
                maxcol = count[level];

            if (que[i]->lchild)
            {
                que[j] = que[i]->lchild;
                order[j] = 2*order[i] ;// i是双亲节点，j是子节点
                j++;
            }
            if (que[i]->rchild)
            {
                que[j] = que[i]->rchild;
                order[j] = 2*order[i]+1;
                j++;
            }
            i++;
        }
    }
    v = maxcol * maxrow;
    return v;
}
int main()
{
    BiTree t;
    createBiTree(t);
    cout << fanmao(t);


    return 0;
}