题意:$2^n$个编号为$1cdots2^n$的人打比赛,这个比赛会给每个人一个唯一的排名,比赛规则递归地定义如下:
$2^n$个人打的是级别为$n$的比赛,初始时他们按某种顺序站成一排
当$n=0$,唯一的一人是第一名
当$ngeq1$,每相邻两个人PK,编号小的人获胜,让$2^{n-1}$个胜者按在原序列中的相对顺序进行级别为$n-1$的比赛,让$2^{n-1}$个败者按在原序列中的相对顺序进行级别为$n-1$的比赛,并将他们的排名加上$2^{n-1}$
可以看出如果初始时的顺序确定了,这样一定可以给所有人一个唯一的排名
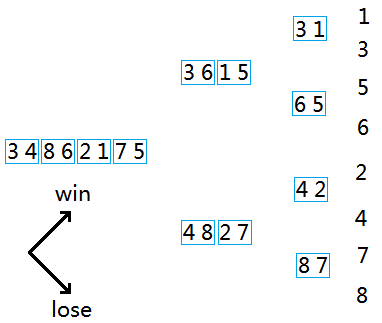
题意不是特别易懂,上图描述了一个打比赛的过程
现在给定一份最终每个人的排名,有一些人的排名还未确定,让你构造一个初始序列使得最终排名和输入相符
以下用从$0$开始的下标和排名
首先,我们可以通过合理安排顺序,使得每次PK都是左边的人赢,考虑把打比赛的过程倒序,那么两个在$n-1$级比赛中排名都为$i$的人会进行一次PK,胜者在$n$级比赛中的排名为$2i$,败者为$2i+1$
然后有一个判定是否有解的结论:如果在一场级别为$n$的比赛中第$i$名的人是$a_i$,那么$a_ilt a_{i+2^j}(i&2^j=0,0leq jlt n)$
考虑用归纳法证明:当$j=0$时显然成立(这是许多场$1$级比赛),设当$jlt n-1$时结论成立
若$i=2k$,那么$i$是两个在$n-1$级比赛中排名都为$k$的人之间的PK胜者,$i+2^{n-1}$是两个在$n-1$级比赛中排名都为$k+2^{n-2}$的人之间的PK胜者,因为两个$n-1$级比赛中都有$a_klt a_{k+2^{n-2}}$,所以$i$是四个人中最强的,也就是说$a_ilt a_{i+2^{n-1}}$
若$i=2k+1$,类似可得$i+2^{n-1}$是最弱的,所以结论成立
有了这个结论,问题转为:给定一个DAG$i ightarrow i+2^j(i&2^j=0)$和部分节点的权值$a_i$,填上剩下的权值使其满足限制$i ightarrow j,a_ilt a_j$
首先正反各扫一遍,得到每个节点的权值的取值范围,这是一个区间
直接贪心即可,从小到大依次填数,填$x$时选择未被选择的区间中满足$Lleq x$且有最小$R$的区间,这个直接按$L$从小到大加入区间,用优先队列维护$R$即可
因为每次都是左边的人赢,即按奇偶性分开,所以最后要像FFT一样把$i$的权值放到$rev_i$去
这个题好神啊...
#include<stdio.h>
#include<queue>
#include<vector>
#include<algorithm>
using namespace std;
int a[262144],rev[262144],lw[262144],hi[262144],val[262144];
struct pr{
int x,y;
pr(int a=0,int b=0){x=a;y=b;}
};
bool operator<(pr a,pr b){return a.x==b.x?a.y>b.y:a.x>b.x;}
priority_queue<pr>q;
vector<pr>e[262144];
int main(){
int n,N,i,j;
scanf("%d",&n);
N=1<<n;
for(i=0;i<N;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(n-1));
for(i=0;i<N;i++){
scanf("%d",a+i);
a[i]--;
}
for(i=N-1;i>=0;i--){
hi[i]=~a[i]?a[i]:N-1;
for(j=0;j<n;j++){
if(~i>>j&1)hi[i]=min(hi[i],hi[i|(1<<j)]);
}
}
for(i=0;i<N;i++){
lw[i]=~a[i]?a[i]:0;
for(j=0;j<n;j++){
if(i>>j&1)lw[i]=max(lw[i],lw[i^(1<<j)]);
}
}
for(i=0;i<N;i++){
if(lw[i]>hi[i]){
puts("NO");
return 0;
}
e[lw[i]].push_back(pr(hi[i],i));
}
for(i=0;i<N;i++){
for(pr t:e[i])q.push(t);
if(q.empty()||q.top().x<i){
puts("NO");
return 0;
}
val[q.top().y]=i;
q.pop();
}
puts("YES");
for(i=0;i<N;i++)printf("%d ",val[rev[i]]+1);
}
转载于:https://www.cnblogs.com/jefflyy/p/9741892.html