% 输入
% m 是l*c矩阵,第i列是第i类分布的平均向量,c表示类别
% S是l*l*c矩阵,第i个二维l*l成分是i类分布的协方差
% P是c维向量,它由类的先验概率组成
% 返回值
% (估计)N列向量的矩阵X,矩阵的每一列都是一个l维数据向量
% 行向量y的每i个表示基于第i个数据向量的类
function[X,y] = generate_gauss_classes(m, S, P, N)
[l, c]=size(m);
X=[];
y=[];
for j=1:c
%从每个分布生成[p(j)*N]向量
t = mvnrnd(m(:, j), S(:, :, j), fix(P(j) * N));
% 由于固定操作,样本总数可能略小于N
X=[X t'];
y=[y ones(1, fix(P(j) * N)) * j];
end
% 输入参数
% m:均值向量
% X:基于上述类的包含列向量的矩阵X
% 输出为一个N维向量,它的第i部分包含一个类,这个类的相应向量是根据最小欧几里得距离给定的
function z = euclidean_classifier(m, X)
[l, c] = size(m);
[l, N] = size(X);
for i = 1:N
for j = 1:c
t(j) = sqrt((X(:, i) - m(:, j))' * (X(:,i) - m(:,j)));
end
[num, z(i)] = min(t);
end
function z = comp_gauss_dens_val(m, S, x)
[l, q] = size(m);
z = (1/((2*pi)^(1/2)*det(S)^0.5))*exp(-0.5*(x-m)'*inv(S)*(x-m));
% 输入参数
% m:均值向量
% X:基于上述类的包含列向量的矩阵X
% 输出为一个N维向量,它的第i部分包含一个类,这个类的相应向量是根据最小欧几里得距离给定的
function z = euclidean_classifier(m, X)
[l, c] = size(m);
[l, N] = size(X);
for i = 1:N
for j = 1:c
t(j) = sqrt((X(:, i) - m(:, j))' * (X(:,i) - m(:,j)));
end
[num, z(i)] = min(t);
end
% 输入参数
% m:均值向量
% S:c类问题的类分布的协方差矩阵
% X:基于上述类的包含列向量的矩阵X
% 输出为一个N维向量,它的第i部分包含一个类,这个类的相应向量是根据最小Mahalanobis距离给定的
function z = mahalanobis_classifier(m, S, X)
[l, c] = size(m);
[l, N] = size(X);
for i = 1:N
for j = 1:c
t(j) = sqrt((X(:, i) - m(:, j))' * inv(S(:, :, j)) * (X(:, i) - m(:, j)));
end
[num, z(i)] = min(t);
end
% 注意:本函数可以处理多达6个不同的类
function plot_mul_group_data(X, y, class_error, title_text, m)
[l, N] = size(X); % N=数据向量的编号,l=维数
[l, c] = size(m); % c=类的编号
[ll, N] = size(y);
if(l ~= 2)
fprintf('NO PLOT CAN BE GENERATED \ n')
return
else
figure(1);
pale = ['r.'; 'g.'; 'b.'; 'y.'; 'm.'; 'c.'];
for k = 1:ll
subplot(2,2,k);
hold on
for i = 1: N
plot(X(1, i), X(2, i), pale(y(k,i), :))
end
% 绘制类均值
for j = 1: c
plot(m(1, j), m(2, j), 'k + ')
end
tt = sprintf('%s(分类错误率:%.3f)', title_text{k}, class_error(k));
title(tt);
end
end
- 上机实验【2.2】(其他题目,注意更换m,S的数据)
randn('seed', 0);
m = [1 1;12 8;16 1]';
S(:,:,1) = [4 0;0 4];
S(:,:,2) = [4 0;0 4];
S(:,:,3) = [4 0;0 4];
P=[1/3;1/3;1/3];
N=1000;
[X1,y] = generate_gauss_classes(m,S,P,N);
% 贝叶斯分类
z1 = bayes_classifier(m, S, P, X1);
ans1 = compute_error(y, z1);
% 欧几里得距离
z2 = euclidean_classifier(m, X1);
ans2 = compute_error(y, z2);
% Mahalanobis距离
z3 = mahalanobis_classifier(m, S, X1);
ans3 = compute_error(y, z3);
% 绘图
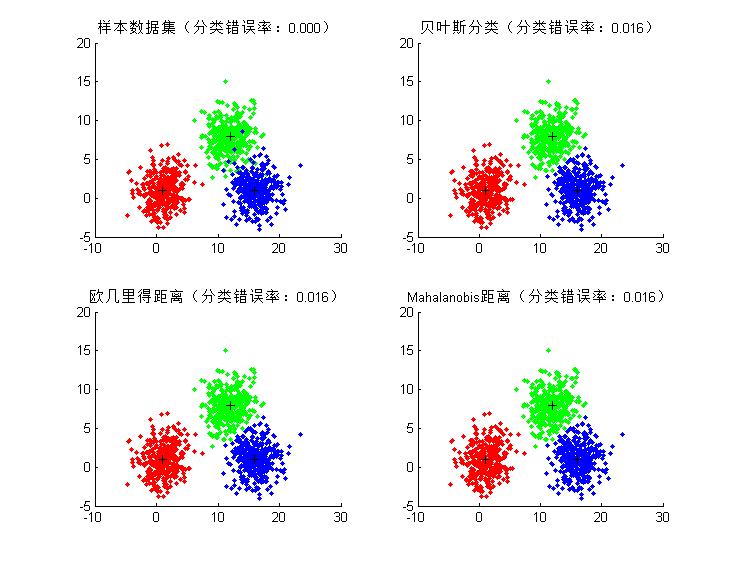
plot_mul_group_data(X1, [y;z1;z2;z3], [0;ans1;ans2;ans3], {'样本数据集';'贝叶斯分类';'欧几里得距离';'Mahalanobis距离'}, m);
- 【2.2】图形结果(参数:m = [1 1;12 8;16 1]'; S = [4 0;0 4]; )
- 【2.3】图形结果(参数:m = [1 1;14 7;16 1]'; S = [5 3;3 4];)

- 【2.4】图形结果(参数:m = [1 1;8 6;13 1]'; S = [6 0;0 6];)
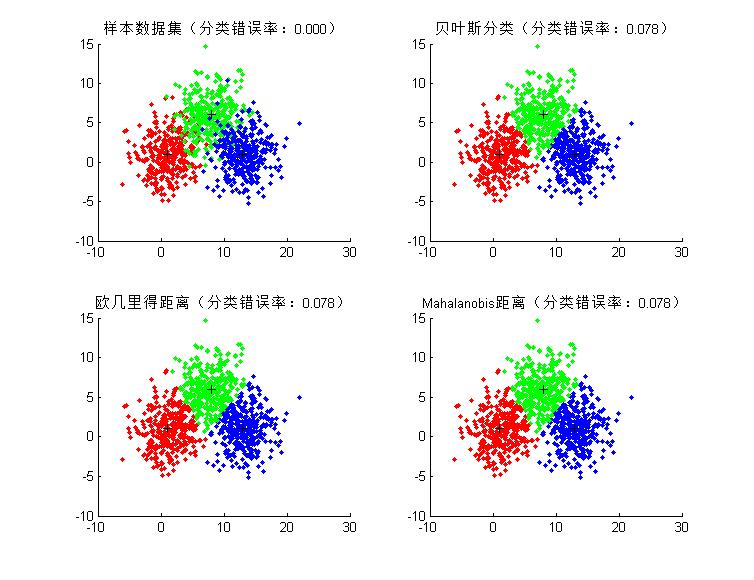
- 【2.5】图形结果(参数:m = [1 1;10 5;11 1]'; S = [7 4;4 5];)




