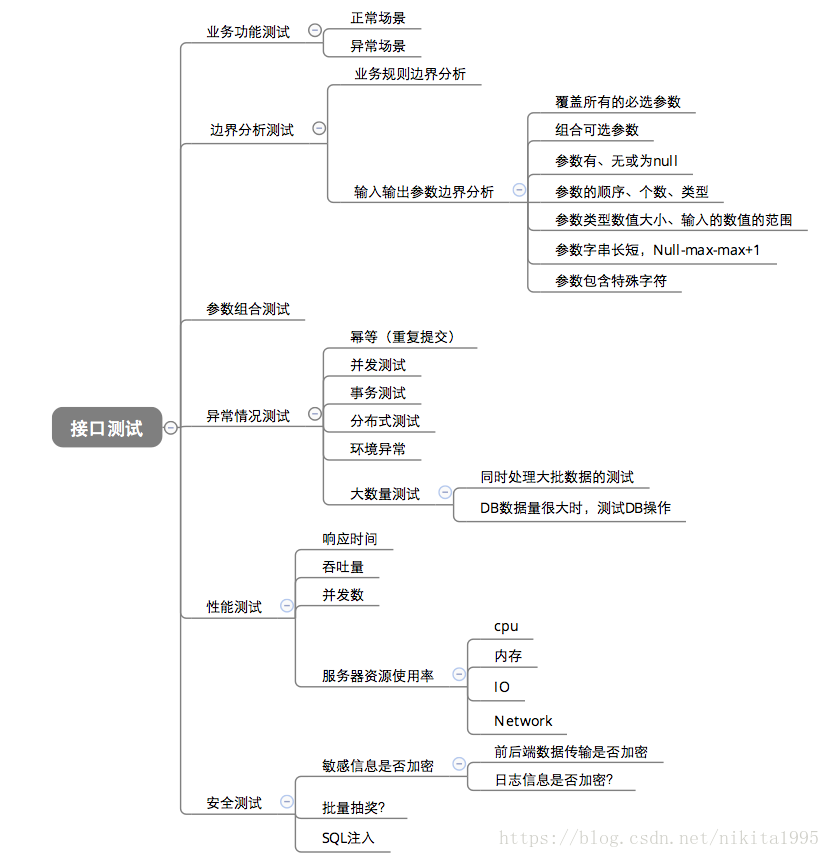
- 功能测试:测试这个接口的功能是否实现,并且测试这个接口是否按照接口文档来进行开发的(比如说接口文档规定了一些关键字,而开大的时候把关键字改成了其他的关键字,因为在整个项目周期,并不只有一个开发而是有多个,所以可能因为在开发过程中因为关键字不一样导致某些开发的功能异常,还有自动化脚本也会发生异常)
- 逻辑业务,主要指的是一些逻辑业务依赖关系(比如支付宝提交订单的时候要保证你是在登录的情况下,如果你没有登录而提交成功了,这就是异常,可以修改请求的cookie来测试)
- 异常测试:参数异常:关键字参数(应用其他的关键字替换进行测试)、参数为空、参数多少(通过添加参数增添个数),参数错误。数据异常:关键字数据(填入的数据用其他的数据语言的数据替用)、数据长度、数据为空、数据错误。
1 输入
输入参数主要从以下几各方面设计:
a 必填项校验
接口文档中有是否必填的说明。参考接口文档即可。
b 参数长度校验
参考接口文档即可。
c 参数值的有效性校验
如:身份证号的校验 ,设计的数据虽然符合身份证号的规则,但是并不是真实有效的身份证号;这种情况就要看身份证号的校验规则是什么样了,一般都是用的现成的身份证号校验器,但是有些是自己写的校验算法,这个本人就遇到过这种问题—校验算法写的不正确;
所以参数有效性的校验就需要结合实际业务场景,判断哪些数据是真实有效的数据,一定要确保所有真实有效的数据是可以验证通过的。
d 参数组合校验
不同的参数组合可能会存在不同的业务场景;
e 如果参数是枚举值,一定要各种枚举值都要测试,因为可能不同的枚举走的不同的业务流程;
f 参数值的默认值的校验
参考接口文档。
g 某些参数具有特定的生成规则,要单独针对生成规则设计用例,一定要保证真实有效的数据是可以验证通过的。
如身份证号中间几位 ***19860701*,本人就遇到过输入***19861001*这种值校验不正确;
2 接口逻辑
接口逻辑我用的设计方法是分支覆盖—>路径覆盖—>场景覆盖,同样也是要结合实际业务场景,根本不发生的业务场景就是无效的测试用例。
a 第一步先把业务流程图画出来;
b 依据路程图中的分支分别设计,不同分支不同的场景,这里就要把异常的场景考虑进去;如接口超时,接口异常,接口请求成功或失败,成功后怎么处理,失败后流程是否继续执行,失败后的数据怎么处理;
以打款接口为例:
打款结果有打款成功或打款失败,成功后怎么处理,需要回写打款成功状态,失败后怎么处理,也需要回写失败状态,失败后的数据可以操作退回,也可以操作重新出款等等;
c 测试逻辑设计完成后要想一想不同的业务场景怎么去测试,需要哪些人员协助,
如接口超时怎么去测试,请求重复怎么去测试,请求并发怎么去测试
3 输出
输入结果:正常输出和异常输出,常用的方法有错误推断法(列举出程序中可能存在的错误或者异常,根据他们选择测试用例)
4 以上都完成后,要结合实际的业务场景去掉冗余的用例(即实际业务场景不存在的流程或者输入数据);
5 如果业务流程涉及到状态转换,要单独设计用户—方法:状态转换图;
6 涉及到多个不同金额或者手续费的计算,可能还会用到正交实验法去设计用例;
7 另外,用例设计中还应当包含异常流程中产生的异常数据的处理流程;—通常所说的补偿机制,这块流程能大大的减轻人工运营的工作量,当然,这需要在做系统设计的时候就需要把这部分考虑进去。
接口测试经常遇到的bug和问题,如下: