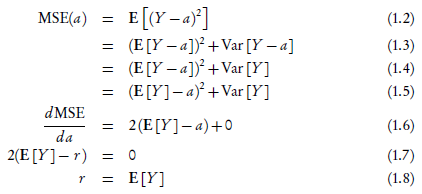Chapter 1 Regression: Predicting and Relating Quantitative Features
1.1 统计学,数据分析,回归
统计学是利用数学来研究和提高从不完整的,有噪声、corrupt、不可复制的和其他因素导致的不完美的数据中刻画可靠的推论的方法。
Paragraph 1 end =================
大多数的科学的学科都是围绕着我们世界的某个部分,或者是我们之中的。
心理学(Psychology)研究思想;地理学(geology)研究地球的组成和形成;经济学研究生产,分配和交换;真菌学(mycology)研究蘑菇。统计学并不研究世界,而是研究我们试图去理解世界的方法——某些供其他学科使用的智慧工具。它的作用并不直观,而是通过帮助其他学科来体现价值。
Paragraph 2 end =================
这种用途是十分重要的,因为所有的学科都必须处理不完美的数据。数据也许并不完美,因为我们只能观察和记录到相关数据的其中一小部分;或者因为,不管我们不管我们多么仔细地尝试,我们的数据总是会包含噪声。在过去的两个世纪中,统计学通过将它们建模成为随机过程来处理所有的这些不完美,并且概率已经称为统计学的中心以至于我们必须刻意的(deliberately)介绍随机事件(as in sample surveys)。
Paragraph 3 end =================
统计学就使用概率论来对数据建模得出推论。我们试图使用数学方式去理解不同过程的来得到推论:在何种条件下它们是可靠的?它们会产生哪种误差,误差频率是多少?当它们有效的时候我们能得到什么?当某些东西出差错的时候会有什么迹象?就像其他的科学一样,比如工程,药学和经济学,统计学不仅仅在于理解,同时也回去改善:我们想要更好的分析数据,更加可靠地,有更少更小的误差,能够在更广泛的条件下,更快地,付出更少的体力劳动。有时候这些目标会产生矛盾——快速、简单的方法也许很容易出错(error-prone),或者说在非常狭隘的条件下才会很可靠。
Paragraph 4 end ================
人们很想知道的是,不同的变量之间是如何关联的,并且统计学中提供的一个核心工具用来了解变量之间的关系就是回归。在36-401(课程)中,你已经学会了如何进行线性回归,了解到了它如何用于数据分析中,也学习了它的属性。在本课程中,我们将在此基础之上构建,在很多方向上扩展基本的线性回归,来回答很多关于变量之间如果关联的问题。
Paragraph 5 end ================
这和预测密切相关。能够预测并不是我们想要知道变量之间关系的唯一原因,有时预测也可以测试我们对于关系的认识。(如果我们理解错了,我们也许仍可以预测,但是很难发现我们如何理解并且不能预测。)所以在超越线性回归的知识之前,先来看一下预测,并且如何从一无所有来预测一个一个变量。然后我们来看一下在变量之间的预测性关系,并且会发现线性回归只是smoothing方法这个大家族中的一个成员而已,这类方法我们都可以使用。
Paragraph 6 end ====================
Section 1.1 end ===================
1.2 猜测随机变量的值
我们有一个数值的,数量的随机变量,我们想象设为Y。我们假设它是一个随机变量,并且试图通过通过猜测一个单值来预测它。(其他类型的预测也是可能的——我们也许会猜测Y是否会落入到某个范围之内,或者它会有其他的可能性,又或者是Y的整个概率分布。但是在后面的课中我们将会学到这也将适用于其他类型的预测。)猜测的最好的值是什么?或者更正常的,Y的最佳预测点是哪个?
Paragraph 7 end ================
为了回答这个问题,我们需要挑选一个函数来进行优化,用来度量我们预测结果的好坏——或者说我们预测的结果有多差,我们得到的误差是多大。一个合理的起点是均方误差(mean squared error):
因此,我们想要找到一个值,r,使得MSE(a)最小。
因此这里我们用均方误差来度量了我们的预测质量,最佳的预测值就是期望值。
1.2.1 预测期望值
当然,为了预测E[Y],我们必须知道Y的期望值。事实上,我们并不知道。然后,如果我们有采样值y1, y2, ..., yn,我们可以从采样的平均值来预测期望:
如果采样的数据是独立同分布的(independent and identically distributed,IID),那么打书定理告诉我们:
并且中心极限定理告诉我们有关于收敛速度的快慢(即平方误差大概是Var[Y]/n)。
当然假设yi是独立同分布的这是一个很强的条件,但是我们可以假设几乎一样的条件,如果它们对于共同的期望值是不相关的。即使它们是相关的,但是相关性减少的足够快,所有的改变为收敛速度。因此"坐下,等着,收敛"是一个预测期望值的非常可靠的方法。
1.3 回归函数
当然,通常预测一个点的值并不十分有用。典型的,在数据中我们有很多的变量。