有点捞的数据结构笔记

单调栈

主要题型

给定一个序列，求在这个序列中每一个数左边/右边，离他最近的数但比他小/大的数是什么

下一个更大元素

简单分析：

• 先从nums2数组中找出每一个数右边第一个比它大的数（使用单调栈）
• 遍历nums1找到其存在于nums2中的元素并进行答案输出（使用哈希表）

假设有7, 22, 20, 8这样的数列，从右往左遍历。8入栈后，遍历到20这个元素。因为20比8大，所以比8小的数一定比20小（满足题目求的下一个大数字的条件），且20比8更近，也就是说这个8一点用也没有了，一切风头都被20占了去，所以8出栈。

......

当遍历到22，依照上方描述，20也出栈，栈空了，此时代表22的右边没有比它大的数，所以返回-1。最后22入栈

class Solution {
public:
    vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
        // 创建哈希表 记录num2中的元素Key和其对应的右边最大数Value
        unordered_map<int, int> hash;
        // 创建单调栈 栈中存的是比 当前遍历到的元素 大的数
        stack<int> stk;
        // 因为是从右边开始找 所以逆序遍历数组
        for (int i = nums2.size() - 1; i >= 0; --i)
        {
            // 找出比它大的数 == 求栈顶元素
            // 因为数组的遍历顺序是逐渐往左走 所以如果遍历到了一个更大的数 就说明这个数不仅能满足条件而且满足优先级更高(更近)的条件
            // 题目中给出了数互不相同的条件 所以无需 >=
            while (!stk.empty() && nums2[i] > stk.top())
                stk.pop();
            // 栈不空 证明有结果 将对应的结果存入哈希表
            if (!stk.empty())
                hash.insert(make_pair(nums2[i], stk.top()));
            else
                hash.insert(make_pair(nums2[i], -1));
            // 遍历到的元素入栈
            stk.push(nums2[i]);
        }
        // 将nums1中的数和哈希表中的比对 有记录则输出结果
        int nums1Size = nums1.size();
        for (int i = 0; i < nums1Size; ++i)
        {
            auto iterator = hash.find(nums1[i]);
            // nums1再利用 节省空间
            if (iterator != hash.end())
                nums1[i] = iterator->second;
        }
        return nums1;
    }
};

每日温度

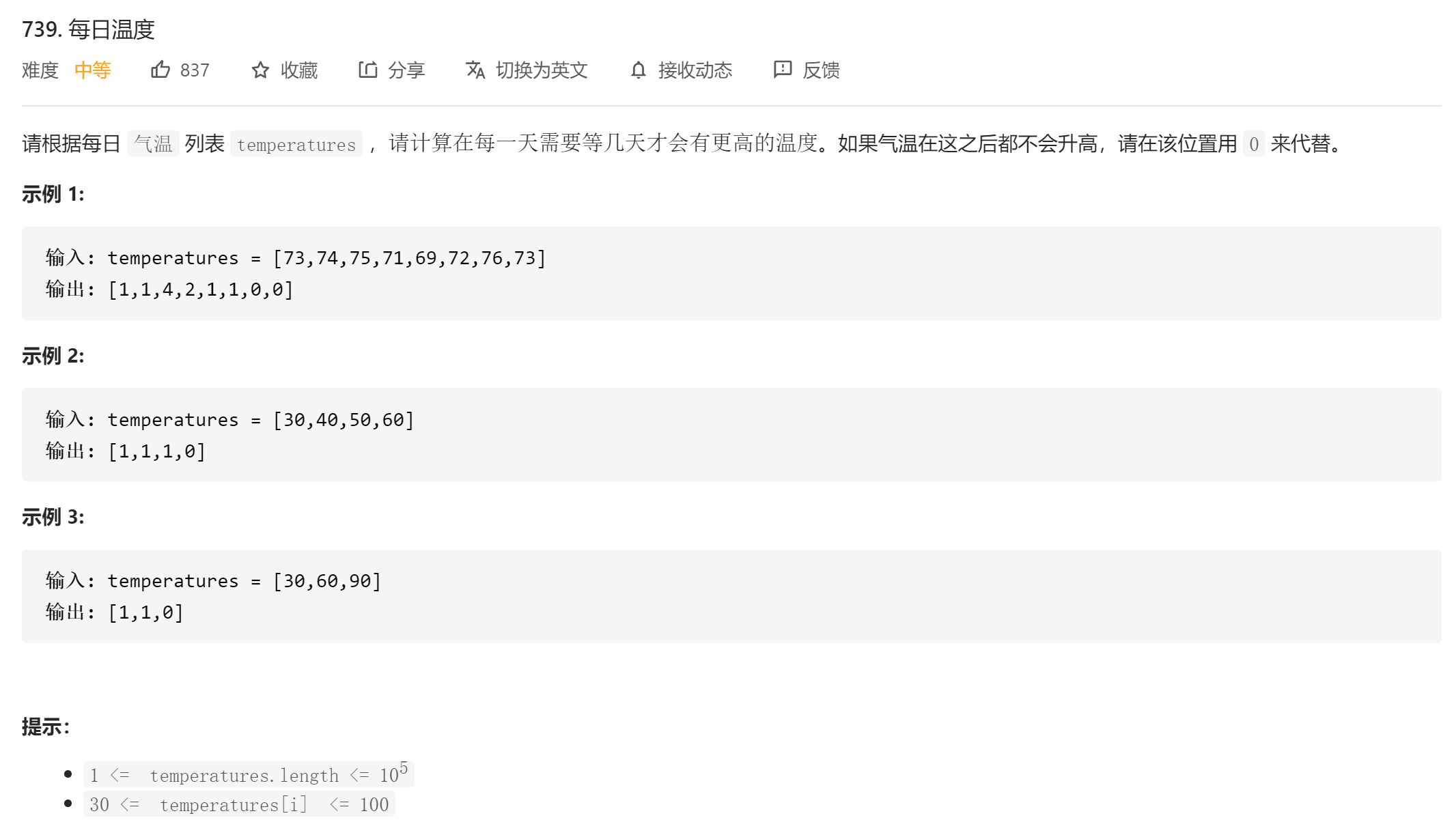
题目分析：题目要求的是某一个数的右边第一个比它大的数

所以使用单调栈，逆序遍历数组

class Solution {
public:
    vector<int> dailyTemperatures(const vector<int>& temperatures) {
        // 单调栈中存的是数的index
        stack<int> stk;
        vector<int> result(temperatures.size());
        for (int i = temperatures.size() - 1; i >= 0; i--)
        {
            // 将不可能用到的元素出栈
            while (!stk.empty() && temperatures[i] >= temperatures[stk.top()])
                stk.pop();
            // 计算结果
            result[i] = stk.empty() ? 0 : stk.top() - i;
            // 将遍历到的元素的index入栈
            stk.push(i);
        }
        return result;
    }
};

小技巧

• 如果是求某个数左边，那么正序遍历数组；如果求的是右边，那么逆序遍历数组

• 出栈的条件为：栈非空 且 大于或小于

  如何判断大于还是小于，把遍历到的那个数写在左边，栈顶的数写在右边，中间的符号为题目给的要求（例如求右边第一个比他大的数，那么符号为>）；是否写等于号根据题意判断

  temperatures[i] >= temperatures[stk.top()]
  

单调队列

滑动窗口

class Solution {
public:
    void slidingWindow(const vector<int>& nums, int k)
    {
        list<int> q;
        int numsSize = nums.size();
        for (int i = 0; i < numsSize; i++)
        {
            // 检测队头是否已经滑出滑动窗口
            if (!q.empty() && i - k == q.front())
                q.pop_front();
            // 扩充活动窗口
            q.push_back(i);
            // 输出窗口内容
            for (auto item : q)
                cout << nums[item] << ends;
            cout << endl;
        }
    }
};

使用list模拟queue，目的是遍历方便，适合Debug

int main()
{
    Solution s;
    // 窗口大小为3
    s.slidingWindow({1,3,-1,-3,5,3,6,7}, 3);
    return 0;
}

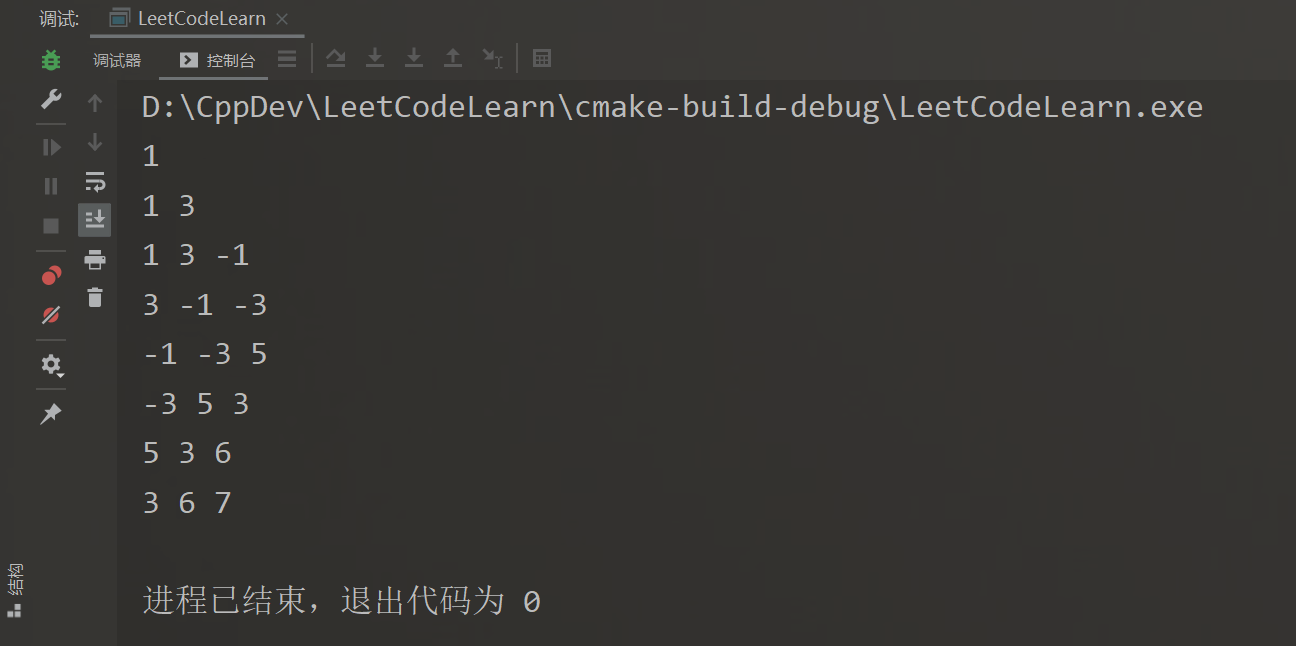
但是一般情况下，我们通常使用右标识来控制滑动窗口。因为实际做题下，双端队列一般优化为单调队列，记录的数据不一定完全按着窗口顺序来

class Solution {
public:
    void maxSlidingWindow(const vector<int>& nums, int k) 
    {
        // 用于Debug输出值才使用的双向链表 实际会使用双端队列
        list<int> l;
        for (int right = 0; right < nums.size(); right++)
        {
            // 加入新元素
            l.push_back(right);
            // 当队列不为空 且滑动窗口的大小超出了界限时 才需要出队
            int left = right - k + 1;
            if (!l.empty() && l.front() < left)
                l.pop_front();
            // 遍历输出
            for (int i = l.front(); i <= right; i++)
                cout << nums[i] << ends;
            cout << endl;
        }
    }
};

滑动窗口最大值

单纯的从滑动窗口的角度出发，每次窗口移动时遍历其中元素，找出最大值，这种是暴力做法

而采用单调队列的方法能够优化滑动窗口问题，降低时间复杂度

• 先判断是否需要循环出队尾，使deque满足单调性
• 新元素入队（窗口的增长）
• 窗口过长部分裁剪

class Solution {
public:
    vector<int> maxSlidingWindow(const vector<int>& nums, int k) {
        // 求最大数 == 求单调队列的队头 => 单调队列为递减队列
        // 单调队列中存放的是index
        deque<int> dq;
        int numsSize = nums.size();
        vector<int> result(numsSize - k + 1);
        for (int right = 0; right < numsSize; right++)
        {
            // 确保队列是单调队列 如果即将加入的元素比队尾的元素要大 则循环出队尾
            while (!dq.empty() && nums[right] >= nums[dq.back()])
                dq.pop_back();
            // 新元素入队
            dq.push_back(right);
            // 当队列不为空 且滑动窗口的大小超出了界限时 才需要出队
            int left = right - k + 1;
            if (!dq.empty() && dq.front() < left)
                dq.pop_front();
            // 当滑动窗口大小增长至k时 才开始记录结果
            // 队头的元素就是最大值的index
            if (right + 1 >= k)
                result[right - k + 1] = nums[dq.front()];
        }
        return result;
    }
};

Trie树-字典树

用来快速存储字符串集合的数据结构

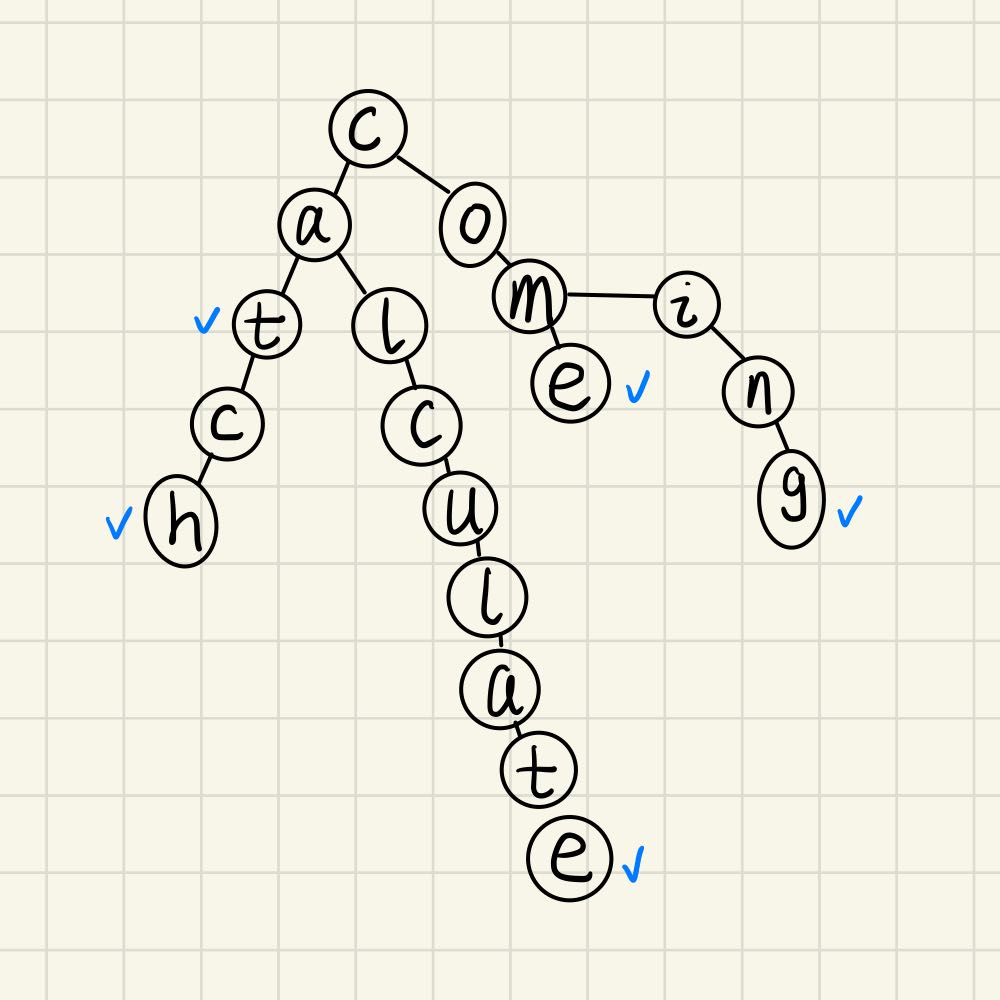
假设只存储小写字母，那么一个节点最多会有26个子节点，那么在初始化的时候先分配这26个空间，但是先置为nullptr

class Trie
{
private:
    struct TrieNode
    {
        bool isEnd;
        vector<shared_ptr<TrieNode>> children;

        TrieNode() : isEnd(false), children(26) {}
    };

    shared_ptr<TrieNode> root;

    shared_ptr<TrieNode> searchPrefix(const string& prefix)
    {
        shared_ptr<TrieNode> current = root;
        for (const char& c : prefix)
        {
            int index = c - 'a';
            if (current->children[index] == nullptr)
                return nullptr;
            current = current->children[index];
        }
        return current;
    }

public:
    Trie() : root(make_shared<TrieNode>()) {}

    void insert(const string& word)
    {
        shared_ptr<TrieNode> current = root;
        for (const char& c : word)
        {
            int index = c - 'a';
            if (current->children[index] == nullptr)
                current->children[index] = make_shared<TrieNode>();
            current = current->children[index];
        }
        current->isEnd = true;
    }

    bool search(const string& word)
    {
        shared_ptr<TrieNode> p = searchPrefix(word);
        return p != nullptr && p->isEnd == true;
    }

    bool startsWith(const string& prefix)
    {
        shared_ptr<TrieNode> p = searchPrefix(prefix);
        return p != nullptr;
    }
};

并查集

简单的示例代码，不考虑合并或者查找的树不在集合中的情况

class UnionFindSet
{
private:
    unordered_map<int, int> parent;
    unordered_map<int, int> size;
public:
    void add(int x)
    {
        parent[x] = x;
        size[x] = 1;
    }

    int find(int x)
    {
        // 路径压缩
        if (parent[x] != x)
            parent[x] = find(parent[x]);
        return parent[x];
    }

    int rootSize(int x)
    {
        return size[find(x)];
    }

    void merge(int x, int y)
    {
        int xRoot = find(x);
        int yRoot = find(y);
        // 如果二者是不同集合的元素
        if (xRoot != yRoot)
        {
            // yRoot成为新的父
            parent[xRoot] = yRoot;
            size[yRoot] += size[xRoot];
        }
    }
};

二叉堆

堆是一个数据集合，是一颗完全二叉树

• 插入一个数
• 求集合中的最小值
• 删除最小值
• 删除任意一个元素
• 修改任意一个元素

小根堆

• up操作接受一个index，小根堆中直接将该位置和父节点比较，如果比父节点小，则说明优先级更高，和父节点互换，称作上浮
• down操作接受一个index，小根堆中先和两个孩子比较（如果有的话），然后选出一个最小的进行互换（除了是自己），和子节点互换，称作下沉

struct MyData
{
    int data;
    MyData(int num) : data(num) {}
    MyData(const MyData& other) { this->data = other.data;}

    bool operator<(const MyData& other) const
    {
        return this->data < other.data;
    }
};

class Heap
{
private:
    vector<MyData> heap;   // 小根堆
public:
    Heap() : heap(1, INT32_MIN) {}

    Heap(const initializer_list<MyData>& tempList) : Heap()
    {
        heap.reserve(tempList.size() + 1);
        for (const auto& num : tempList)
            heap.push_back(num);
        // 建堆
        for (int i = (heap.size() - 1) / 2; i >= 1; i--)
            down(i);
    }

    int size() { return heap.size() - 1; }

    void insert(int num)
    {
        // 在末端插入
        heap.push_back(num);
        // 末端元素上浮
        up(heap.size() - 1);
    }

    const MyData& front()
    {
        if (heap.size() < 2)
            throw exception("Heap is Empty");
        return heap[1];
    }

    void pop_front()
    {
        if (heap.size() < 2)
            throw exception("Heap is Empty");
        // 让最顶层的和最底层的交换
        heap[1] = heap[heap.size() - 1];
        heap.pop_back();
        // 让顶层元素下沉
        down(1);
    }

private:
    void up(int index)
    {
        int father = index / 2;
        // 直接和根节点比较
        if (father > 0 && heap[father] > heap[index])
        {
            // 互换
            ::swap(heap[father], heap[index]);
            up(father);
        }
    }

    void down(int index)
    {
        int minIndex = index;
        // 判断根节点和左节点的大小
        if (index * 2 < heap.size() && heap[index * 2] < heap[minIndex])
            minIndex = index * 2;
        // 判断根节点和右节点的大小
        if (index * 2 + 1 < heap.size() && heap[index * 2 + 1] < heap[minIndex])
            minIndex = index * 2 + 1;
        // 如果和左右节点的比较有结果
        if (minIndex != index)
        {
            // 互换
            ::swap(heap[minIndex], heap[index]);
            down(minIndex);
        }
    }
};

int main()
{
    Heap h({1, 2, 3 ,4 ,2, -1});
    int heapSize = h.size();
    for (int i = 0; i < heapSize; i++)
    {
        cout << h.front().data << ends;
        h.pop_front();
    }
}

大根堆和小根堆的实现可以说是一样的，只是在down和up操作时将每个节点的比较颠倒一下就可以，又或者有这个究极偷懒方法

bool operator<(const MyData& other) const
{
    // 反向比较
    return this->data > other.data;
}

优先队列

这里实现一个int类型的，队头为大元素的优先队列（其实就是大根堆，几乎和上面的代码一摸一样）

class PriorityQueue
{
private:
    vector<int> heap;

    void down(int index)
    {
        int maxIndex = index;
        if (index * 2 < heap.size() && heap[index * 2] > heap[maxIndex])
            maxIndex = index * 2;
        if (index * 2 + 1 < heap.size() && heap[index * 2 + 1] > heap[maxIndex])
            maxIndex = index * 2 + 1;
        if (maxIndex == index)
            return;
        ::swap(heap[index], heap[maxIndex]);
        down(maxIndex);
    }

    void up(int index)
    {
        int father = index / 2;
        if (father > 0 && heap[father] < heap[index])
        {
            ::swap(heap[father], heap[index]);
            up(father);
        }
    }
public:
    PriorityQueue() : heap(1, INT32_MAX) {}

    void push_back(int data)
    {
        heap.push_back(data);
        up(heap.size() - 1);
    }

    void pop_front()
    {
        // 将最后一个数和队头的元素互换 然后移除最后一个数
        if (heap.size() <= 1) return;
        heap[1] = heap[heap.size() - 1];
        heap.pop_back();
        down(1);
    }

    const int& top()
    {
        if (heap.size() > 1)
            return heap[1];
        throw exception("out of range");
    }

    int size()
    {
        return heap.size() - 1;
    }

    bool empty()
    {
        return size() == 0;
    }
};

哈希表

哈希表基类

template<typename realType, typename storeType = realType>
class BaseHashSet
{
protected:
    // 储存int类型的数据
    vector<vector<storeType>> hashVec;

    inline virtual int get_hash_code(const realType& data) = 0;
    inline virtual storeType get_mapping_value(const realType& data) = 0;
public:
    BaseHashSet() = default;

    void insert(realType data)
    {
        int code = get_hash_code(data);
        hashVec[code].push_back(get_mapping_value(data));
    }

    bool find(realType data)
    {
        int code = get_hash_code(data);
        return any_of(hashVec[code].begin(), hashVec[code].end(), [&data, this](const storeType& i) 
        {
            return i == get_mapping_value(data); 
        });
    }
};

template<typename T>
class HashSet : public BaseHashSet<T>
{
};

int类型的哈希表

说是哈希表，其实是简陋到家的unordered_set<int>，采用链地址法解决冲突。modValue的取值遵循以下几点

• 最好是质数，且离2^n越远越好
• movValue的值不能过大也不能过小（大概是当前数量级的一半？例如10^9和105）
• 哈希数组的大小和modValue的大小一致

template<>
class HashSet<int> : public BaseHashSet<int>
{
private:
    int modValue;
protected:
    inline virtual int get_hash_code(const int& data) override
    {
        return (data % modValue + modValue) % modValue;
    }

    inline virtual int get_mapping_value(const int& data) override
    {
        return data;
    }

public:
    HashSet(int _modValue = 13) : modValue(_modValue), hashVec(_modValue) {}
};

string类型的哈希表

先将string映射为unsigned long long，当种子取质数133时，可以近似认为映射得来的数是独一无二的。然后再将映射后的值取模求index，最后存入哈希数组中

template<>
class HashSet<string> : public BaseHashSet<string, unsigned long long>
{
private:
    const int seed = 133;
    int modValue;
protected:
    inline virtual int get_hash_code(const string& data) override
    {
        // 将映射值取模后存入哈希表中
        unsigned long long mappingValue = get_mapping_value(data);
        return (int)(mappingValue % modValue);
    }

    inline virtual unsigned long long get_mapping_value(const string& data) override
    {
        // 映射为unsigned long long
        unsigned long long result = 0;
        for (const char& c : data)
            result = result * seed + c;
        return result;
    }
public:
    HashSet(int _modValue = 13) : modValue(_modValue), hashVec(_modValue) {}
};

树

树的专有名词解析（待完成）

左旋右旋

度

高度

深度

平衡

二叉树

前序中序后序遍历

二叉树的解题模板基本都是围绕三种遍历方式展开的，用的最多的是先序遍历和后序遍历。递归遍历的代码很简单，这里就不演示了，需要掌握的是各种遍历方式究竟能遍历个什么东西出来

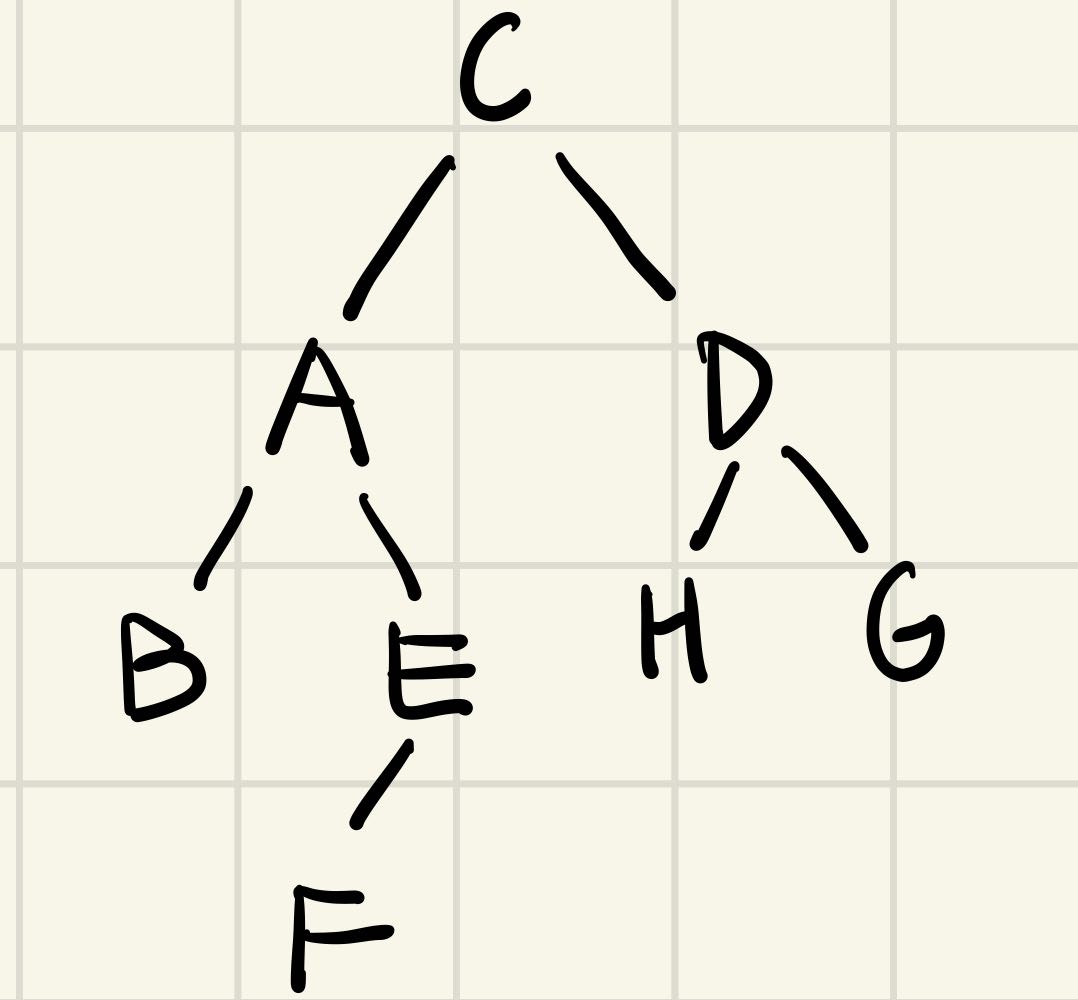
• 前序遍历：C A B E F D H G （根左右）
• 中序遍历：B A F E C H D G （左根右）
• 后序遍历：B F E A H G D C （左右根）

根据前中序遍历构建树

两个知识点

• 前序遍历的第一位是根节点，后续遍历最后一位是根节点
• 中序遍历中某个节点将其左右两端分为左右子树

设有前序遍历为ACDEFHGB，中序遍历为DECAHFBG树，将它构建出来

• 首先前序遍历的第一位是A，所以根节点是A
• 然后在中序中找到A，观察它的左右两边，分别为左右两个子树（左子树的元素有DEC，右子树的元素有HFBG，不分顺序）
• 在左右两个子树的元素中，找到最先在前序遍历中出现的，为子树的根（DEC三者中C最先在前序中出现，HFBG中F最先出现）
• 循环第二第三步骤

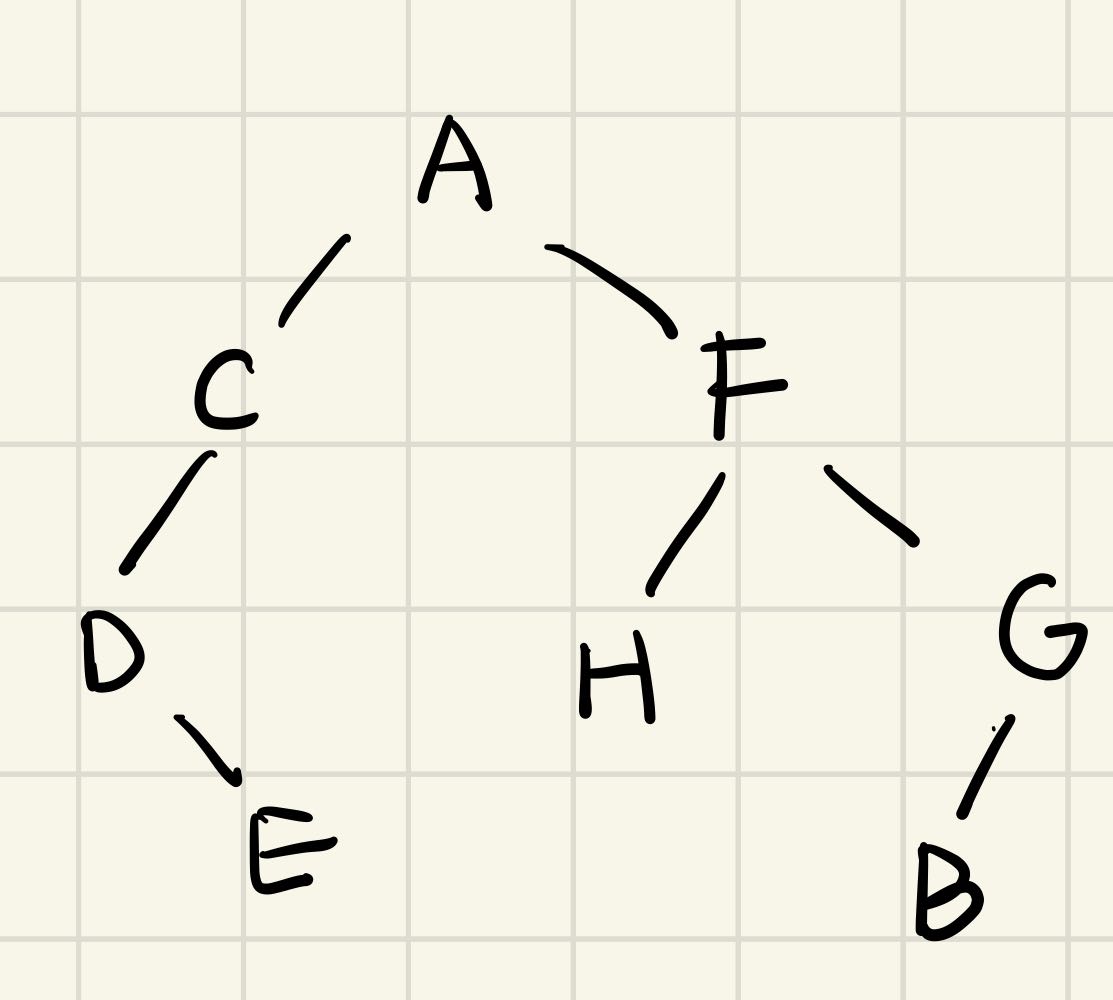
且后序遍历为：EDCHBGFA

class Solution {
public:
    unordered_map<int, int> inorderMap;
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int inorderSize = inorder.size();
        // 记录中序遍历索引
        for (int i = 0; i < inorderSize; i++)
            inorderMap.insert(make_pair(inorder[i], i));
        return build(preorder, 0, inorderSize - 1, inorder, 0, inorderSize - 1);
    }

    TreeNode* build(vector<int>& preorder, int preStart, int preEnd,
        vector<int>& inorder, int inStart, int inEnd)
    {
        if (preStart > preEnd)
            return nullptr;
        int rootValue = preorder[preStart];
        int rootValueIndex = inorderMap[rootValue];
        TreeNode* newNode = new TreeNode(rootValue);
        int leftChildNum = rootValueIndex - inStart;
        int rightChildNum = inEnd - rootValueIndex;
        
        newNode->left = build(preorder, preStart + 1, preStart + leftChildNum, inorder, inStart, rootValueIndex - 1);
        int newPreEnd = preStart + leftChildNum;
        newNode->right = build(preorder, newPreEnd + 1, newPreEnd + rightChildNum, inorder, rootValueIndex + 1, inEnd);
        return newNode;
    }
};

寻找重复的子树

框架规划很简单，分为两个步骤

• 分清需要使用哪种遍历方式。前序是不知道孩子节点的情况的；而后序是知道孩子节点的情况的。前序访问的第一个点为根节点
• 两行递归的前/后写出的代码是针对”根节点“的操作，具体是哪里的”根“，要看递归的深度

class Solution {
public:
    unordered_map<string, int> cachedMap;
    vector<TreeNode*> result;

    vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {
        Traverse(root);
        return result;        
    }

    string Traverse(TreeNode* node)
    {
        if (node == nullptr)
            return "#";
        string leftStr = Traverse(node->left);
        string rightStr = Traverse(node->right);

        string newTree = to_string(node->val) + "," + leftStr + "," + rightStr;
        auto it = cachedMap.find(newTree);
        if (it != cachedMap.end())
        {
            if (it->second == 1)
                result.push_back(node);
            it->second++;
        }
        else
            cachedMap.insert(make_pair(newTree, 1));
        return newTree;
    }
};

这种做法是将树转换为字符串的形式储存在哈希表中，记录的信息为：

优化解法为

class Solution {
public:
    int index = 1;
    unordered_map<string, int> str2Index;
    unordered_map<int, int> index2Num;
    vector<TreeNode*> result;

    vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {
        Traverse(root);
        return result;        
    }

    int Traverse(TreeNode* node)
    {
        if (node == nullptr)
            return 0;
        int leftIndex = Traverse(node->left);
        int rightIndex = Traverse(node->right);
        string str = to_string(node->val) + to_string(leftIndex) + to_string(rightIndex);
        // 树第一次出现
        if (str2Index.find(str) == str2Index.end())
            str2Index.insert(make_pair(str, index++));
        // 获取树的编号
        int oldIndex = str2Index[str];
        if (index2Num.find(oldIndex) == index2Num.end())
            index2Num.insert(make_pair(oldIndex, 0));
        if (++index2Num[oldIndex] == 2)
            result.push_back(node);
        return oldIndex;            
    }
};

假设有这么一颗树

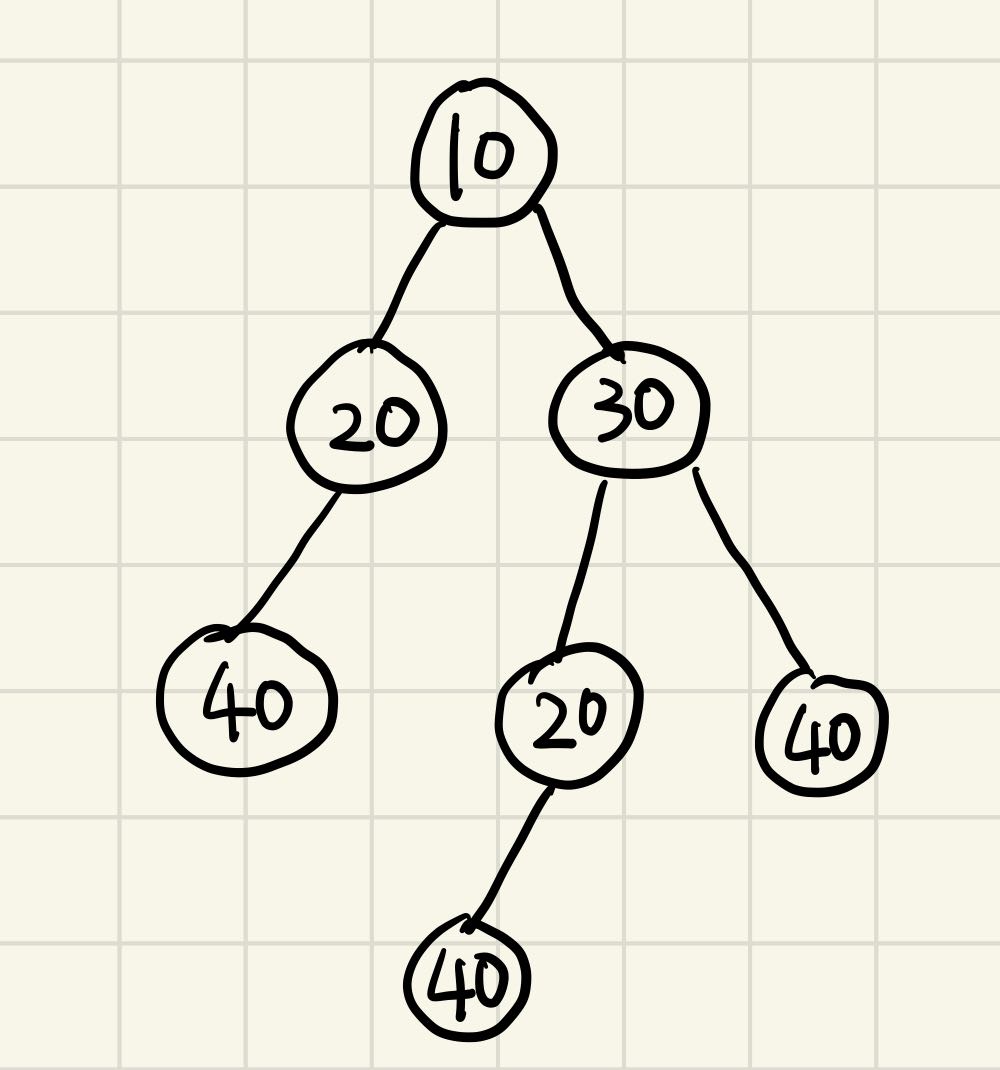
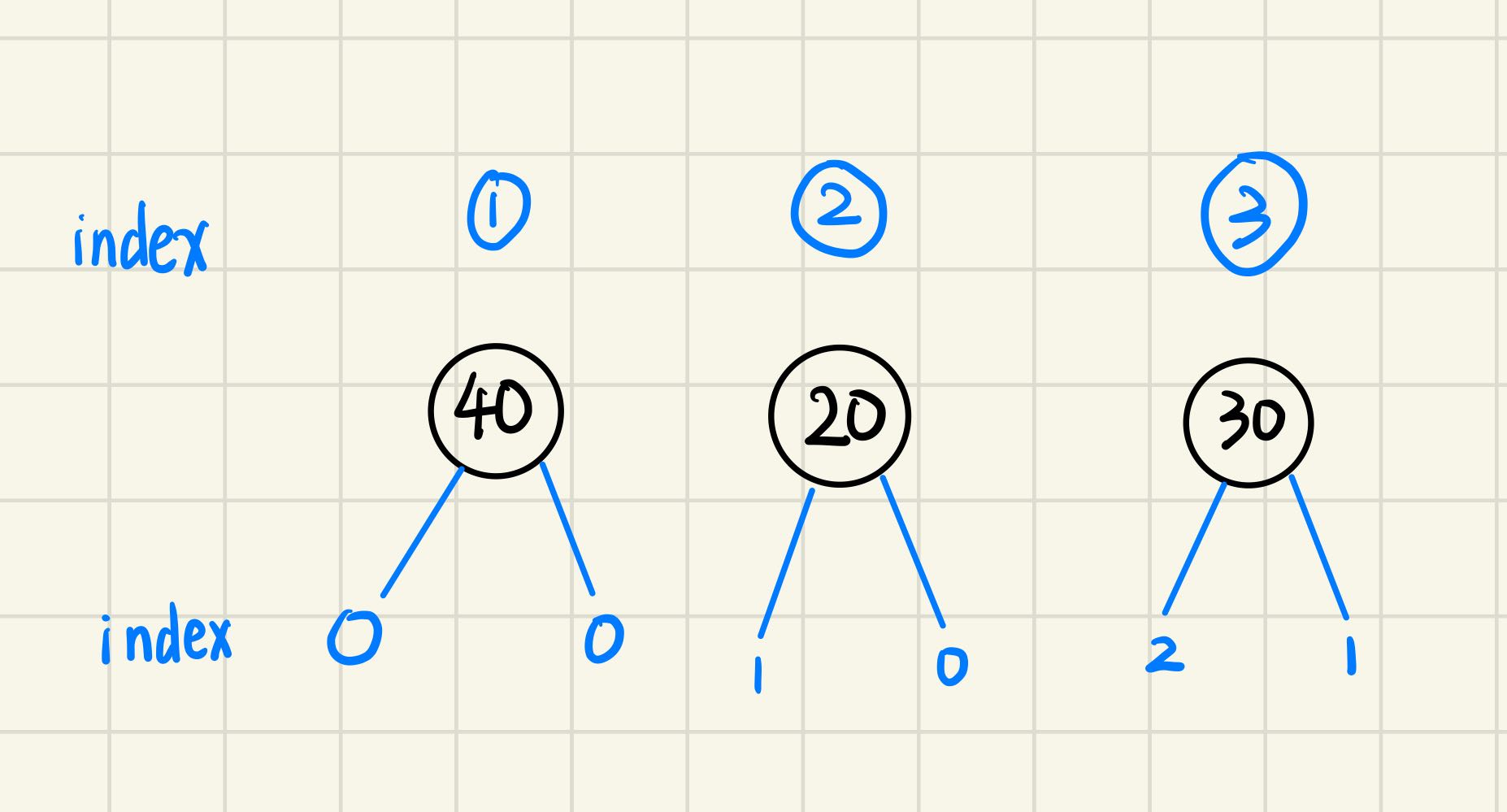
经过遍历后，哈希表中存的数据编程一个“3位的int值”，同时value为该树的编号。比如二号树，它的根节点为值20，左孩子为编号为1的树，右孩子为编号为0的树，即没有右孩子

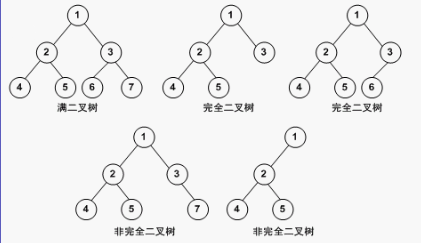
完全二叉树

完全二叉树：每一层都是有序的从左向右排列

满二叉树：每一层都是满的

如何求二叉树的节点

由于二叉树的节点排列没有顺序可言，所以只能暴力遍历，时间复杂度为O(n)

int countNodes(TreeNode* node)
{
    if (node == nullptr)
        return 0;
    return countNodes(node->left) + countNodes(node->right) + 1;
}

如何求满二叉树的节点

由于满二叉树每一层的节点数都是满的，时间复杂度为O(logn)

int countNodes(TreeNode* node)
{
    // 求满二叉树的高度
    int height = 0;
    while (node != nullptr)
    {
        height++;
        // 因为是满二叉树 所以遍历左节点和右节点都一样
        node = node->left;
    }
    return ::pow(2, height) - 1;
}

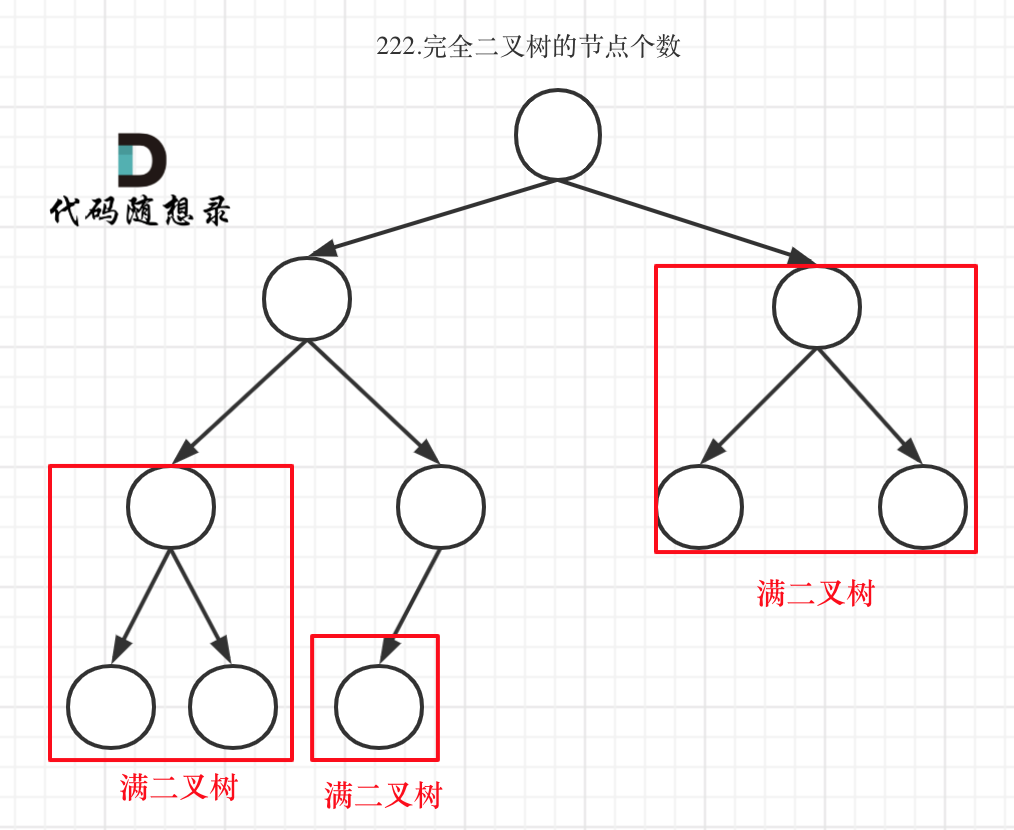
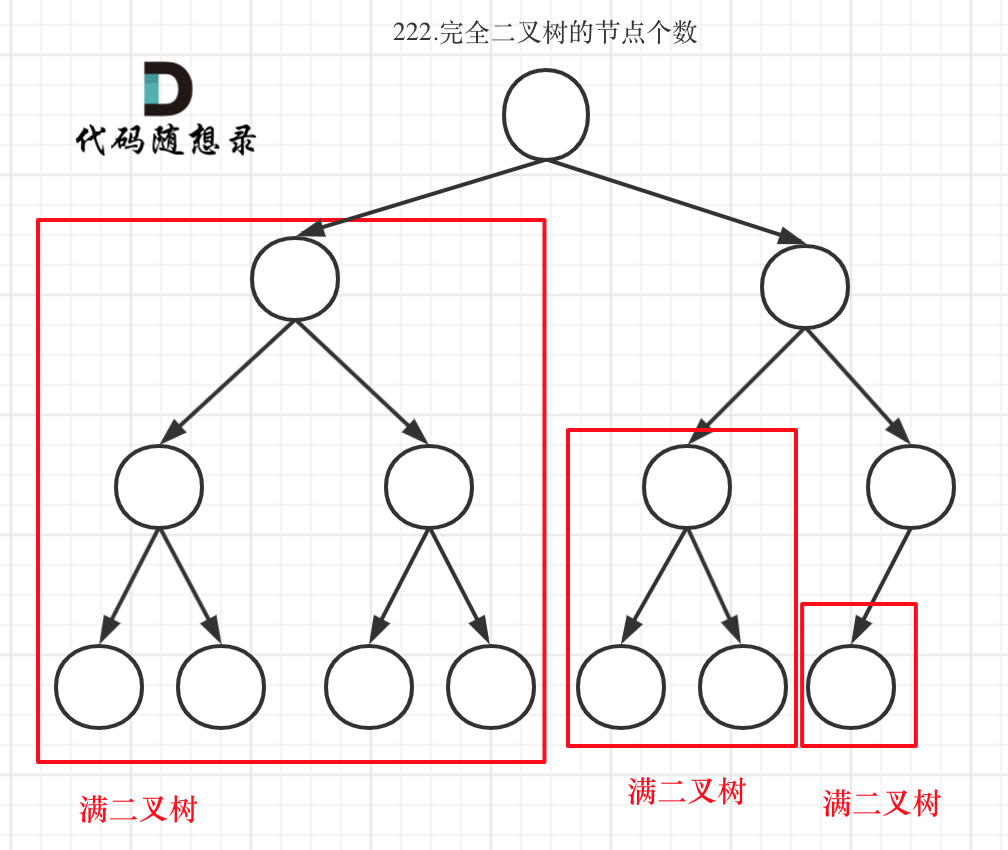
如何求完全二叉树的节点

不管是什么样的完全二叉树，它的左右子树中一定有一个是完全二叉树，一个是满二叉树。而对于完全二叉子树而言，一定又有完全二叉子子树和满二叉子子树。

其中的完全二叉树还可能是一颗满二叉树

int countNodes(TreeNode* root) 
{
    int leftHeight = 0, rightHeight = 0;
    TreeNode* leftNode = root;
    TreeNode* rightNode = root;
    while (leftNode != nullptr)
    {
        leftNode = leftNode->left;
        leftHeight++;
    }
    while (rightNode != nullptr)
    {
        rightNode = rightNode->right;
        rightHeight++;
    }
    // 是满二叉树
    if (leftHeight == rightHeight)
        return pow(2, leftHeight) - 1;
    return countNodes(root->left) + countNodes(root->right) + 1;
}

二叉搜索树（BST）

Binary-Search-Tree

对于任意一个节点来说，它的值必须大于左子树所有的节点，且必须小于右子树所有的节点。并且整棵树中没有相同的数据

拓展性质：

• 从某根节点沿着左下方一直延申，数据越来越小；沿着右下方一直延申，数据越来越大
• 任何子树都是BST
• BST进行中序遍历将会得到有序数列（升序）

验证树是二叉树

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        // 使用long防止被卡数据
        return isValid(root, LONG_MIN, LONG_MAX);
    }

    bool isValid(TreeNode* root, long min, long max)
    {
        if (root == nullptr)
            return true;
        if (root->val <= min || root->val >= max)
            return false;
        return isValid(root->left, min, root->val) && isValid(root->right, root->val, max);
    }
};

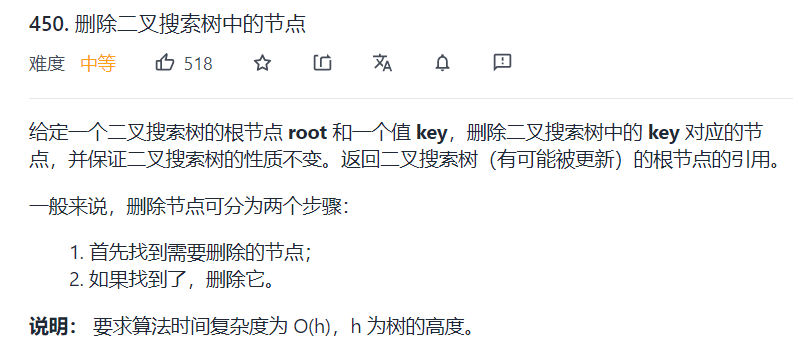
删除操作

• 如果是叶子节点则直接删除
• 如果只有一个节点则直接将子节点替换上去
• 如果有两个节点则通过中序遍历找到待删除节点的下一个节点，然后替换

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == nullptr)
            return nullptr;
        if (root->val > key)
            root->left = deleteNode(root->left, key);
        else if (root->val < key)
            root->right = deleteNode(root->right, key);
        else
        {
            if (root->left == nullptr)
                return root->right;
            if (root->right == nullptr)
                return root->left;
            auto minNode = getMin(root->right);
            root->val = minNode->val;
            root->right = deleteNode(root->right, minNode->val);
        }
        return root;
    }

    TreeNode* getMin(TreeNode* curNode)
    {
        while (curNode->left != nullptr)
            curNode = curNode->left;
        return curNode;
    }
};

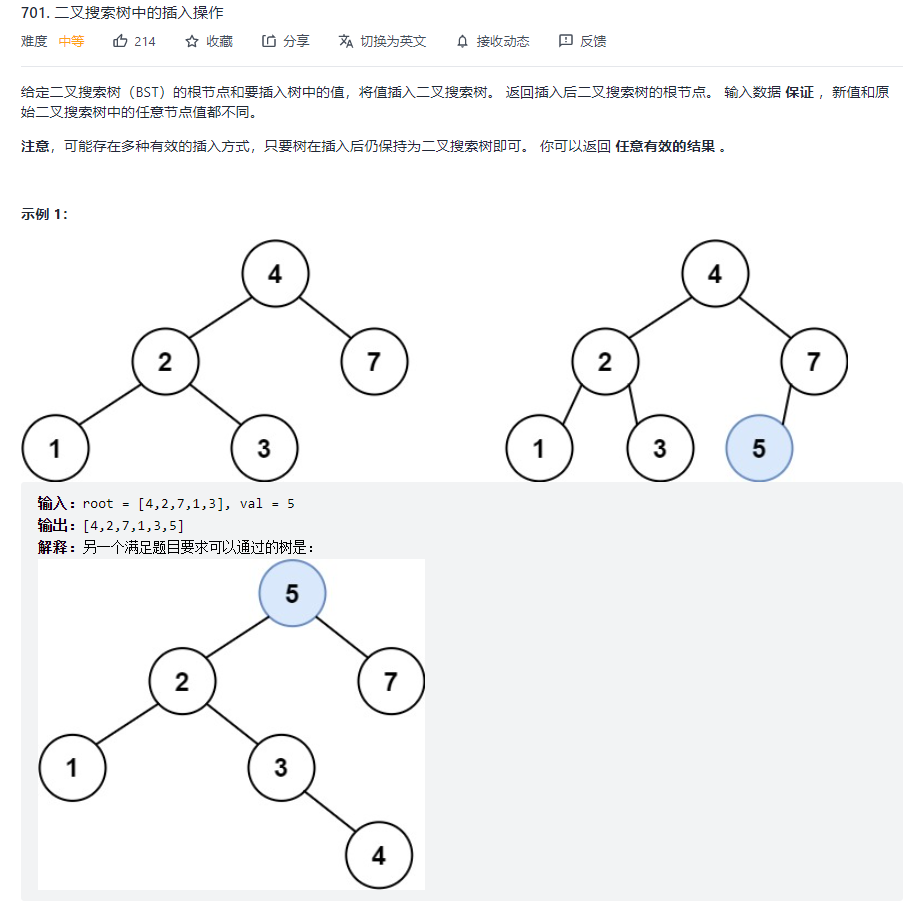
查找操作

• 最好的情况：该树为二叉平衡搜索树，搜索时间复杂度为O(logn)，与二分查找相同
• 最坏的情况：该树为链表（所有节点只有一个孩子），搜索时间复杂度为O(n)

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == nullptr)
            root = new TreeNode(val);
        if (root->val > val)
            root->left = insertIntoBST(root->left, val);
        else if (root->val < val)
            root->right = insertIntoBST(root->right, val);
        return root;
    }
};

二叉平衡搜索树（AVL树）（待完成）

AVL树中所有的节点的左右子树的高度差不超过1

LRU结构

少壮不努力老大徒伤悲，LRU结构使用双向链表和哈希表来实现。通过维护节点顺序来列出最久未使用节点，通过哈希表加速链表的访问，以空间换时间

使用STL中的容器实现，不管是速度还是空间上表现都比较一般

class LRUCache {
public:
    struct MyData
    {
        int key;
        int value;
        MyData() : key(0), value(0) {}
        MyData(int _key, int _value) : key(_key), value(_value) {}
    };

    list<MyData> cacheList;
    unordered_map<int, list<MyData>::iterator> key2ListMap;
    int cacheSize;

    LRUCache(int capacity) : cacheSize(capacity) {}

    int get(int key)
    {
        if (key2ListMap.find(key) != key2ListMap.end())
        {
            // 调用到数据 优先级上升 插到队头
            auto& pData = key2ListMap[key];
            cacheList.emplace_front(pData->key, pData->value);
            cacheList.erase(pData);
            pData = cacheList.begin();
            return pData->value;
        }
        return -1;
    }

    void put(int key, int value)
    {
        // 已经在列表中 更新值 移动到队尾
        if (key2ListMap.find(key) != key2ListMap.end())
        {
            auto& pData = key2ListMap[key];
            pData->value = value;
            cacheList.emplace_front(pData->key, pData->value);
            cacheList.erase(pData);
            pData = cacheList.begin();
        }
        else
        {
            // 还有空间
            if (cacheList.size() < cacheSize)
            {
                cacheList.emplace_front(key, value);
                key2ListMap[key] = cacheList.begin();
            }
            // 没有空间
            else
            {
                // 链表队尾的为最久未使用的元素
                key2ListMap.erase(cacheList.back().key);
                cacheList.pop_back();
                cacheList.emplace_front(key, value);
                key2ListMap[key] = cacheList.begin();
            }
        }
    }
};

使用自建的数据结构实现，哈希表的执行速率和占用空间都不如STL自带的。因此推荐自己重写双向链表，然后用STL的unordered_map

双向链表的设计使用了“虚拟”的头尾节点，在插入和删除的时候方便很多

struct LRUData
{
    int key;
    int value;
    LRUData() = default;
    LRUData(int _key, int _value) : key(_key), value(_value) {}
    LRUData(LRUData&& _lruData) : key(_lruData.key), value(_lruData.value) {}
};

template<typename T>
struct DoubleLinkNode
{
    T data;
    DoubleLinkNode* next;
    DoubleLinkNode* pre;
    DoubleLinkNode() = default;
    explicit DoubleLinkNode(T&& _data, DoubleLinkNode* _next = nullptr, DoubleLinkNode* _pre = nullptr) :
        data(std::move(_data)), next(_next), pre(_pre) {}
};

template<typename T>
class DoubleLinkList
{
public:
    using Node = DoubleLinkNode<T>;
private:
    int listSize;
    Node* begin;
    Node* end;

public:
    DoubleLinkList() : listSize(0), begin(new Node()), end(new Node())
    {
        begin->next = end;
        end->pre = begin;
    }

    ~DoubleLinkList()
    {
        Node* pCurrent = begin;
        while (pCurrent->next != nullptr)
        {
            pCurrent = pCurrent->next;
            delete pCurrent->pre;
        }
        delete end;
    }

    inline int size() { return listSize; }

    void move_to_front(Node* node)
    {
        if (begin->next == node)
            return;
        node->pre->next = node->next;
        node->next->pre = node->pre;

        node->next = begin->next;
        node->pre = begin;

        begin->next->pre = node;
        begin->next = node;
    }

    Node* push_front(T&& data)
    {
        Node* pInsertNode = new Node(std::move(data), begin->next, begin);
        listSize++;
        pInsertNode->next->pre = pInsertNode;
        begin->next = pInsertNode;
        return pInsertNode;
    }


    void pop_back()
    {
        if (listSize == 0)
            return;
        Node* pDeleteNode = end->pre;
        // 上一节点指向结尾
        pDeleteNode->pre->next = end;
        // 结尾指向上一节点
        end->pre = pDeleteNode->pre;
        listSize--;
        delete pDeleteNode;
    }

    T& back()
    {
        // 判断节点数量
        if (listSize > 0)
            return end->pre->data;
        throw exception();
    }
};

template<typename T>
class HashMap
{
private:
    int modValue;
    vector<forward_list<pair<int, T>>> hashVec;

    inline int get_hash_code(int key)
    {
        return (key % modValue + modValue) % modValue;
    }

public:
    explicit HashMap(int _modValue = 53) : modValue(_modValue), hashVec(_modValue) {}

    bool find(int key)
    {
        int hashCode = get_hash_code(key);
        return any_of(hashVec[hashCode].begin(), hashVec[hashCode].end(), [&key](const pair<int, T>& dataPair)
        {
            return dataPair.first == key;
        });
    }

    void erase(int key)
    {
        int hashCode = get_hash_code(key);
        typename forward_list<pair<int, T>>::iterator p = hashVec[hashCode].before_begin();
        for (auto iterator = hashVec[hashCode].begin(); iterator != hashVec[hashCode].end(); ++iterator)
        {
            if (iterator->first == key)
            {
                hashVec[hashCode].erase_after(p);
                return;
            }
            p++;
        }
    }

    void insert(int key, T value)
    {
        int hashCode = get_hash_code(key);
        hashVec[hashCode].emplace_front(key, value);
    }

    T& operator[](int key)
    {
        for (pair<int, T>& dataPair : hashVec[get_hash_code(key)])
        {
            if (dataPair.first == key)
                return dataPair.second;
        }
        throw exception();
    }

};

class LRUCache {
public:
    DoubleLinkList<LRUData> linkList;
    HashMap<DoubleLinkNode<LRUData>*> key2PointerMap;
    int maxCapacity;

    LRUCache(int capacity) : maxCapacity(capacity), linkList(), key2PointerMap(503) {}

    int get(int key)
    {
        if (key2PointerMap.find(key) == true)
        {
            // 将该数据更新为最近刚刚使用过
            linkList.move_to_front(key2PointerMap[key]);
            // 返回找到的数据
            return key2PointerMap[key]->data.value;
        }
        return -1;
    }

    void put(int key, int value)
    {
        if (key2PointerMap.find(key) == true)
        {
            // 数据更新
            key2PointerMap[key]->data.value = value;
            // 将该数据更新为最近刚刚使用过
            linkList.move_to_front(key2PointerMap[key]);
        }
        else
        {
            // 最新数据 插入到链表头
            key2PointerMap.insert(key, linkList.push_front(LRUData(key, value)));
            // 判断是否过长
            if (linkList.size() > maxCapacity)
            {
                // 删除标记
                key2PointerMap.erase(linkList.back().key);
                // 删除尾部元素
                linkList.pop_back();
            }
        }
    }
};