《机器学习》西瓜书第六章支持向量机

支持向量机分为：线性可分支持向量机、线性支持向量机、非线性支持向量机

线性可分支持向量机：训练数据线性可分，通过硬间隔最大化，学习一个线性的分类器；

线性支持向量机：训练数据近似线性可分，通过软间隔最大化，学习一个线性分类器

非线性支持向量机：训练数据线性不可分，通过使用核技巧以及软间隔最大化，学习一个非线性支持向量机。

6.1 间隔与支持向量

在样本空间中，划分超平面课通过如下线性方程来描述：  ω^T x+ b = 0   其中ω = （ω1；ω2；...；ω_d  ）为法向量，决定超平面的方向；b为位移向量，决定超平面与原点之间的距离。

样本空间中任意点x到超平面（ω，b）的距离为      

,距离超平面最近的几个训练样本点，使该式等号成立，他们被称为“支持向量”，两个异类支持向量到超平面距离之和为  2/||ω||，他被称为“间隔”。

支持向量机的基本型 ：

6.2 对偶问题

 我们希望求解式6.6得到大间隔划分超平面所对应的模型

对式6.6添加拉格朗日乘子α_i≥0,则该问题的拉格朗日函数可写为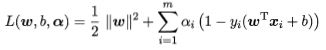，对ω和b求偏导为0，带入后得式6.6的对偶问题：

支持向量机的重要性质：训练完成后，大部分的训练样本都不需要保留，最终模型仅与支持向量有关。

6.3  核函数

原始样本空间内也许并不存在一个能正确划分两类样本的超平面，对于这样的问题，可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。

 定理 6.1（核函数）令χ为输入空间，Κ（.，.）是定义在χ x χ上的对称函数，则k是核函数当且仅当对于任意数据D={x₁,x₂,...,x_m}，核矩阵K总是半正定的。只要有一个对称函数所对应的核函数半正定，它就能作为核函数使用。

若k_1、 k₂为核函数，则其线性组合也是核函数；

若k_1、 k₂为核函数，则核的直积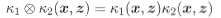也是核函数；

若k_{1为核函数，则对于任意函数g(x),也是核函数。}

6.4  软间隔与正则化

软间隔：允许某些样本不满足约束。当然在最大化间隔的同时，不满足约束的样本应尽可能小。于是，优化目标应写为：

 C>0是一个常数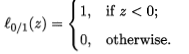，是“0/1损失函数”。

替代损失函数：

 常用的“软间隔支持向量机”：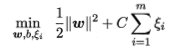

 如果使用对率损失函数来替代0/1损失函数，则几乎就得到了对率回归模型。实际上，支持向量机与对率回归的优化目标相近，通常情况下性能也相当。对率回归上午优势在于其输出具有自然的概率意义而支持向量机不具有概率意义。概率回归能直接应用于多分类任务，支持向量机则需对此进行推广。另一方面，hinge损失有一块“平坦”的零区域，使得支持向量机的解具有稀疏性，而对率损失则是光滑的单调递减函数。不能导出类似支持向量的概念。因此对率回归的解决依赖于更多的训练样本，其预测开销更大。

优化目标中的第一项用来描述划分平面的“间隔”大小，另一项用来表述训练集上的误差。，其中Ω（f）称为“结构风险”，用于描述魔性的某些性质；第二项称为“经验风险”，用于描述模型与训练数据的契合程度；C用于对二者进行折中。

6.5  支持向量回归 SVR

  支持向量回归假设我们能容忍f(x)与y之间最多有ε的偏差，仅当f(x)与y之间差别的绝对值大于ε才计算损失。

6.6 核方法

 给定训练样本，若不考虑偏移项b，则无论SVM还是SVR，学得的模型总能表示成核函数的线性组合。