唯一矩形排除法的几种情况
详细解说参见:http://www.sudopedia.org/wiki/Uniqueness_Test (英文)
在进行游戏的时候,在矩形排除观察之前,应该先使用数对法进行一次排除。 以下7种类型的唯一矩形,对第六种和第七种都还不是很明白是怎么推的,等弄明白后再说明是如何得出论断的
第一种情况
组成矩形的四个方块内,都由候选数xy组成,但是其中一个多了一个一个候选数z,则该数格就必然是z。
这是因为倘若该格不是z的话,则四个方格都由xy组成,形成多解,所以该格必然是z。
第二种情况
由xy组成的矩形上,倘若在其中一边的两个数格还都有另外一个候选数z,则这两个数格必有其中一个为z(倘若两个都不是z,又要出现多解!)
所以在这两个数格所在的house(行/列/块)里必定不能再出现z
第三种情况
跟第二种情况类似,但是这两个数格内不是同一个候选数,而是候选数a,b。此时可以把这两个数格看做一个只含有候选数a和b的数格,它可以与house内的另外的数格一起组成显式数集,从而排除其他数格里的候选数
第四种情况
这又是第三种情况的另外一种特例。假设a和b所在行/列里,别的数格里不包含x,则在xya,xyb这两个数格里,必然包含有a或b以及x,所以必然不包含y!
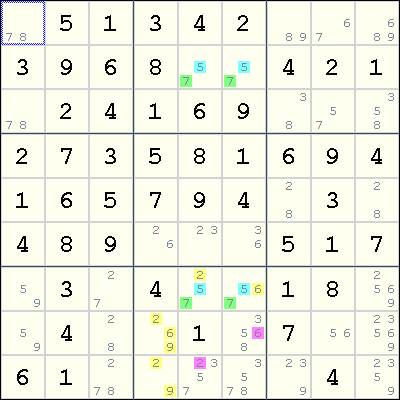
第五种情况
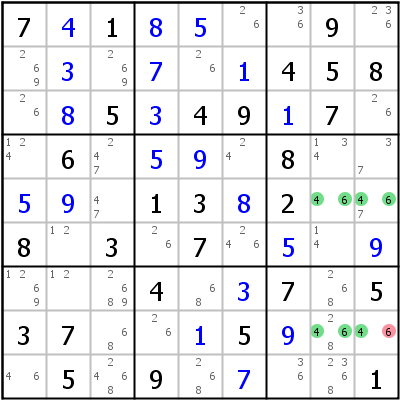
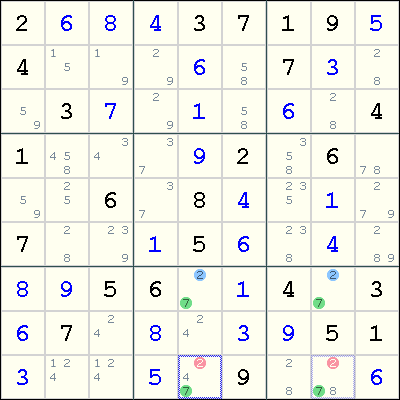
第六种情况
这种矩形要求四个格都含有xy,且其中在两行两列上x只出现在这两个数格里(实际上只要x在行列上形成强链即可推论),且在四个方格的存在对角是xy的情况,则另外两个对角必然不是x。
- 首先为了避免出现多解的情况,这四个方格中,一定会有一个非xy的候选数
- 假定其中一个有额外候选数的数格是x,那么同边的数格就肯定没有x,于是对角数格肯定就是x(因为这两个x是强链),所以对角方格必然不能是非xy的候选数,这显然违背了四个方格肯定有一个非xy候选数的推论矛盾,所以这个假设是错误的。也就是说这个假定是x的数格肯定不能是x。
- 反方向也是同样的推理过程!
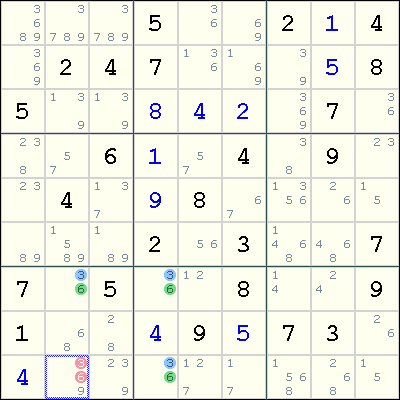
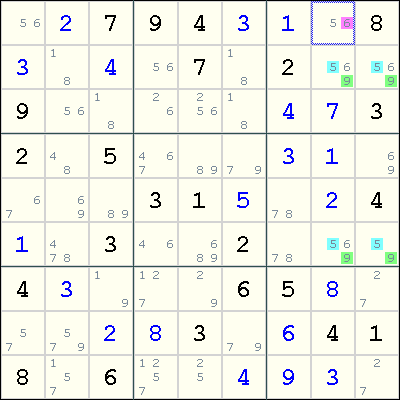
第七种情况
假设我们有一个A,B,C,D数格组成的矩形,A和D在对角,B和C在对角,且AB或BD在同一个BOX里,且他们各自的候选数满足这样的情况: A为ab,B为abx,C为aby,D为abz,其中x,y表示1个以上的候选数,z表示0个以上的候选数xyz可以存在相同的候选数。假定在B和D共同的house里,候选数a只在B和D出现,C和D的共同的house里,a也只在C和D出现,这个时候我们就可以从D里排除候选数b 观察上图,可以在行1行2和列2列6(即r1c26,r2c26)发现Hidden Unique Rectangle,候选数4在第二行和第六列没有在其余第数格出现,且r1c2只有4和8,所以可以从r2c6排除8 在上例中,A是r1c2,B和C是r1c6和r2c2,D是r2c6,a是4,b是8,x和y是3和9,z是2
推理如下:
- 首先为了避免出现多解的情况,这四个方格中,一定会有一个非ab的候选数
- 假定D方格内的数字为b,则D方格不能是a,则B和C里的a因为与D的a是强连接,所以B和C里就一定是a,这就使得在A,B,C,D里不会出现非ab的情况,这显然与之前的推论矛盾,所以D方格不能有数字b
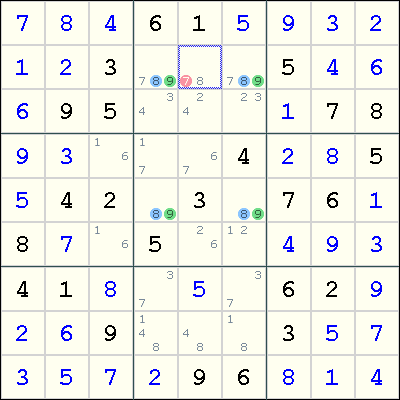
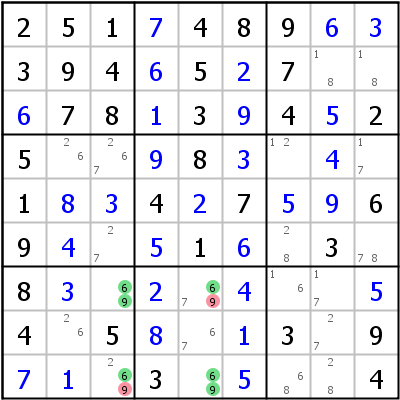
下图是z表示无候选数的情况