对连通图进行遍历,过程中所经过的边和顶点的组合可看做是一棵普通树,通常称为生成树。
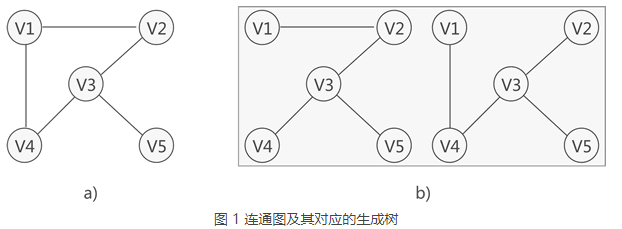
如图 1 所示,图 1a) 是一张连通图,图 1b) 是其对应的 2 种生成树。 连通图中,由于任意两顶点之间可能含有多条通路,遍历连通图的方式有多种,往往一张连通图可能有多种不同的生成树与之对应。 连通图中的生成树必须满足以下 2 个条件: 包含连通图中所有的顶点; 任意两顶点之间有且仅有一条通路; 因此,连通图的生成树具有这样的特征,即生成树中边的数量 = 顶点数 - 1。
生成森林 生成树是对应连通图来说,而生成森林是对应非连通图来说的。 我们知道,非连通图可分解为多个连通分量,而每个连通分量又各自对应多个生成树(至少是 1 棵),因此与整个非连通图相对应的,是由多棵生成树组成的生成森林。

