吴裕雄--天生自然神经网络与深度学习实战Python+Keras+TensorFlow：使用导函数求函数的最小值

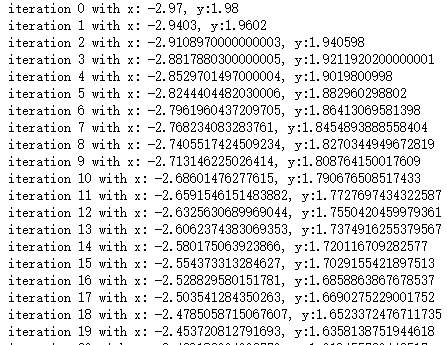
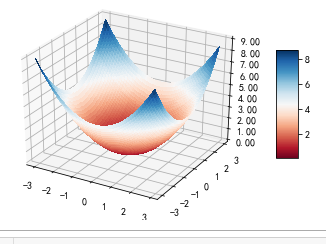
import numpy as np
from matplotlib import cm
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.ticker import LinearLocator, FormatStrFormatter

#设定要绘制的函数
def z_func(x,y):
     return ((x**2+y**2)/2)
    
#设定函数的取值范围
x = np.arange(-3.0,3.0,0.1)
y = np.arange(-3.0,3.0,0.1)

#绘制空间坐标轴
X,Y = np.meshgrid(x, y) # grid of point
#将取值范围内每一点输入函数获得输出以便绘制图像
Z = z_func(X, Y) # evaluation of the function on the grid
fig = plt.figure()
ax = fig.gca(projection='3d')
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.RdBu,linewidth=0, antialiased=False)

ax.zaxis.set_major_locator(LinearLocator(10))
ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))

fig.colorbar(surf, shrink=0.5, aspect=5)

plt.show()

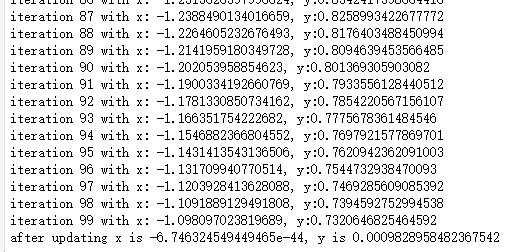
#随意选择一个点出发，然后使用迭代法不断地逼近最小值
#连续调整改进变量值10000次
epoch = 10000
x = -3
prev_x = 0
y = 2
prev_y = 0
r = 0.01
precision = 0.00001

'''
函数(x**2+y**2)/2对x,y的偏导数分别为fx=x,fy=y
'''
for i in range(0, epoch):
    '''
     如果变量改变后的值与改变前的值相差不超过precision，那么停止更新变量
    '''
    stop_x = False
    stop_y = False
    if(abs(prev_x-x)<precision):
        stop_x = True
        #print("x stop in {0} iteration, x: {1}", i, x)
    else:
        prev_x = x-3
        x = x - r * (x)
    if abs(prev_y - y) < precision:
        stop_y = True
        #print("y stop in {0} iteration", i)
    else:
        prev_y = y
        y = y - r * (y)
    
    if stop_x and stop_y:
        print("stop in {0} interations".format(i))
        break   

    if i < 100:
        print("iteration {0} with x: {1}, y:{2}".format(i, x, y))
        
print("after updating x is {0}, y is {1}".format(x,y))