# 导入第三方包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn import metrics
# 随机生成三组二元正态分布随机数
np.random.seed(1234)
mean1 = [0.5, 0.5]
cov1 = [[0.3, 0], [0, 0.3]]
x1, y1 = np.random.multivariate_normal(mean1, cov1, 1000).T
print(x1.shape)
print(y1.shape)
mean2 = [0, 8]
cov2 = [[1.5, 0], [0, 1]]
x2, y2 = np.random.multivariate_normal(mean2, cov2, 1000).T
mean3 = [8, 4]
cov3 = [[1.5, 0], [0, 1]]
x3, y3 = np.random.multivariate_normal(mean3, cov3, 1000).T
# 绘制三组数据的散点图
plt.scatter(x1,y1)
plt.scatter(x2,y2)
plt.scatter(x3,y3)
# 显示图形
plt.show()

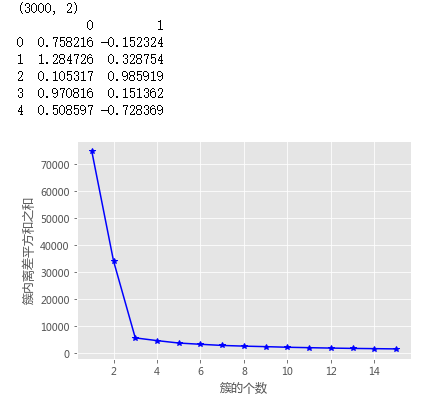
# 构造自定义函数,用于绘制不同k值和对应总的簇内离差平方和的折线图
def k_SSE(X, clusters):
# 选择连续的K种不同的值
K = range(1,clusters+1)
# 构建空列表用于存储总的簇内离差平方和
TSSE = []
for k in K:
# 用于存储各个簇内离差平方和
SSE = []
kmeans = KMeans(n_clusters=k)
kmeans.fit(X)
# 返回簇标签
labels = kmeans.labels_
# 返回簇中心
centers = kmeans.cluster_centers_
# 计算各簇样本的离差平方和,并保存到列表中
for label in set(labels):
SSE.append(np.sum((X.loc[labels == label,]-centers[label,:])**2))
# 计算总的簇内离差平方和
TSSE.append(np.sum(SSE))
# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 设置绘图风格
plt.style.use('ggplot')
# 绘制K的个数与GSSE的关系
plt.plot(K, TSSE, 'b*-')
plt.xlabel('簇的个数')
plt.ylabel('簇内离差平方和之和')
# 显示图形
plt.show()
# 将三组数据集汇总到数据框中
X = pd.DataFrame(np.concatenate([np.array([x1,y1]),np.array([x2,y2]),np.array([x3,y3])], axis = 1).T)
print(X.shape)
print(X.head())
# 自定义函数的调用
k_SSE(X, 15)
# 构造自定义函数,用于绘制不同k值和对应轮廓系数的折线图
def k_silhouette(X, clusters):
K = range(2,clusters+1)
# 构建空列表,用于存储个中簇数下的轮廓系数
S = []
for k in K:
kmeans = KMeans(n_clusters=k)
kmeans.fit(X)
labels = kmeans.labels_
# 调用字模块metrics中的silhouette_score函数,计算轮廓系数
S.append(metrics.silhouette_score(X, labels, metric='euclidean'))
# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 设置绘图风格
plt.style.use('ggplot')
# 绘制K的个数与轮廓系数的关系
plt.plot(K, S, 'b*-')
plt.xlabel('簇的个数')
plt.ylabel('轮廓系数')
# 显示图形
plt.show()
# 自定义函数的调用
k_silhouette(X, 15)

# 自定义函数,计算簇内任意两样本之间的欧氏距离
def short_pair_wise_D(each_cluster):
mu = each_cluster.mean(axis = 0)
Dk = sum(sum((each_cluster - mu)**2)) * 2.0 * each_cluster.shape[0]
return Dk
# 计算簇内的Wk值
def compute_Wk(data, classfication_result):
Wk = 0
label_set = set(classfication_result)
for label in label_set:
each_cluster = data[classfication_result == label, :]
Wk = Wk + short_pair_wise_D(each_cluster)/(2.0*each_cluster.shape[0])
return Wk
# 计算GAP统计量
def gap_statistic(X, B=10, K=range(1,11), N_init = 10):
# 将输入数据集转换为数组
X = np.array(X)
# 生成B组参照数据
shape = X.shape
tops = X.max(axis=0)
bots = X.min(axis=0)
dists = np.matrix(np.diag(tops-bots))
rands = np.random.random_sample(size=(B,shape[0],shape[1]))
for i in range(B):
rands[i,:,:] = rands[i,:,:]*dists+bots
# 自定义0元素的数组,用于存储gaps、Wks和Wkbs
gaps = np.zeros(len(K))
Wks = np.zeros(len(K))
Wkbs = np.zeros((len(K),B))
# 循环不同的k值,
for idxk, k in enumerate(K):
k_means = KMeans(n_clusters=k)
k_means.fit(X)
classfication_result = k_means.labels_
# 将所有簇内的Wk存储起来
Wks[idxk] = compute_Wk(X,classfication_result)
# 通过循环,计算每一个参照数据集下的各簇Wk值
for i in range(B):
Xb = rands[i,:,:]
k_means.fit(Xb)
classfication_result_b = k_means.labels_
Wkbs[idxk,i] = compute_Wk(Xb,classfication_result_b)
# 计算gaps、sd_ks、sk和gapDiff
gaps = (np.log(Wkbs)).mean(axis = 1) - np.log(Wks)
sd_ks = np.std(np.log(Wkbs), axis=1)
sk = sd_ks*np.sqrt(1+1.0/B)
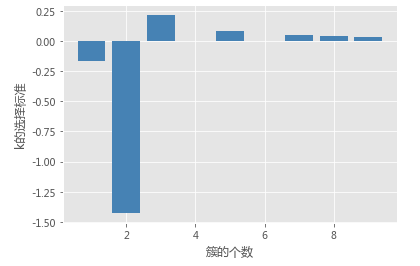
# 用于判别最佳k的标准,当gapDiff首次为正时,对应的k即为目标值
gapDiff = gaps[:-1] - gaps[1:] + sk[1:]
# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 设置绘图风格
plt.style.use('ggplot')
# 绘制gapDiff的条形图
plt.bar(np.arange(len(gapDiff))+1, gapDiff, color = 'steelblue')
plt.xlabel('簇的个数')
plt.ylabel('k的选择标准')
plt.show()
# 自定义函数的调用
gap_statistic(X)
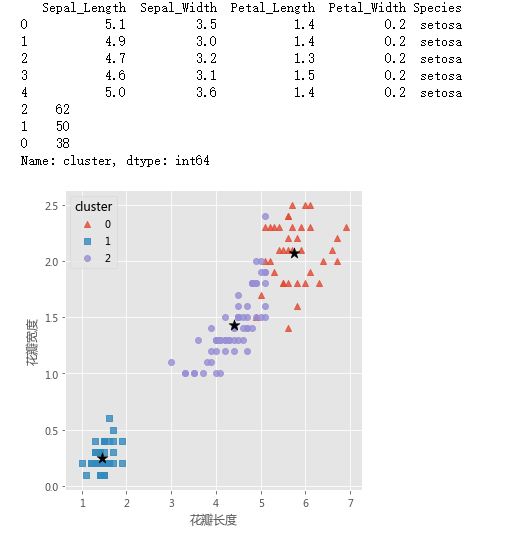
# 读取iris数据集
iris = pd.read_csv(r'F:\python_Data_analysis_and_mining\15\iris.csv')
# 查看数据集的前几行
print(iris.head())
# 提取出用于建模的数据集X
X = iris.drop(labels = 'Species', axis = 1)
# 构建Kmeans模型
kmeans = KMeans(n_clusters = 3)
kmeans.fit(X)
# 聚类结果标签
X['cluster'] = kmeans.labels_
# 各类频数统计
a = X.cluster.value_counts()
print(a)
# 导入第三方模块
import seaborn as sns
# 三个簇的簇中心
centers = kmeans.cluster_centers_
# 绘制聚类效果的散点图
sns.lmplot(x = 'Petal_Length', y = 'Petal_Width', hue = 'cluster', markers = ['^','s','o'],
data = X, fit_reg = False, scatter_kws = {'alpha':0.8}, legend_out = False)
plt.scatter(centers[:,2], centers[:,3], marker = '*', color = 'black', s = 130)
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
# 图形显示
plt.show()
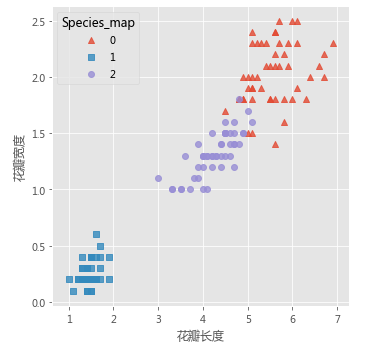
# 增加一个辅助列,将不同的花种映射到0,1,2三种值,目的方便后面图形的对比
iris['Species_map'] = iris.Species.map({'virginica':0,'setosa':1,'versicolor':2})
# 绘制原始数据三个类别的散点图
sns.lmplot(x = 'Petal_Length', y = 'Petal_Width', hue = 'Species_map', data = iris, markers = ['^','s','o'],
fit_reg = False, scatter_kws = {'alpha':0.8}, legend_out = False)
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
# 图形显示
plt.show()
# 导入第三方模块
import pygal
# 调用Radar这个类,并设置雷达图的填充,及数据范围
radar_chart = pygal.Radar(fill = True)
# 添加雷达图各顶点的名称
radar_chart.x_labels = ['花萼长度','花萼宽度','花瓣长度','花瓣宽度']
# 绘制三个雷达图区域,代表三个簇中心的指标值
radar_chart.add('C1', centers[0])
radar_chart.add('C2', centers[1])
radar_chart.add('C3', centers[2])
# 保存图像
radar_chart.render_to_file('E:\radar_chart.svg')
# 读取球员数据
players = pd.read_csv(r'F:\python_Data_analysis_and_mining\15\players.csv')
print(players.shape)
print(players.head())
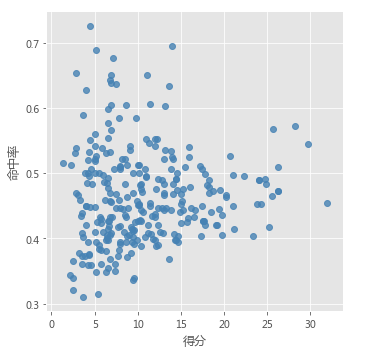
# 绘制得分与命中率的散点图
sns.lmplot(x = '得分', y = '命中率', data = players,
fit_reg = False, scatter_kws = {'alpha':0.8, 'color': 'steelblue'})
plt.show()

from sklearn import preprocessing
# 数据标准化处理
X = preprocessing.minmax_scale(players[['得分','罚球命中率','命中率','三分命中率']])
# 将数组转换为数据框
X = pd.DataFrame(X, columns=['得分','罚球命中率','命中率','三分命中率'])
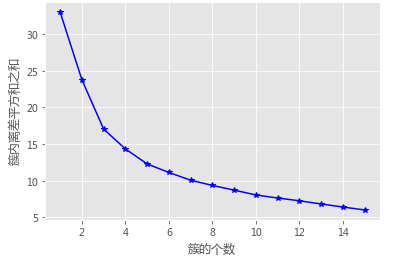
# 使用拐点法选择最佳的K值
k_SSE(X, 15)
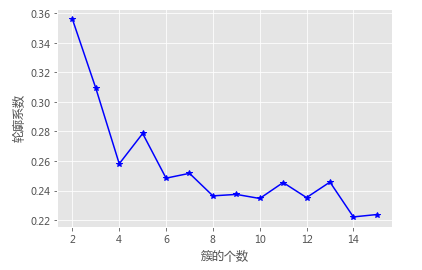
# 使用轮廓系数选择最佳的K值
k_silhouette(X, 15)
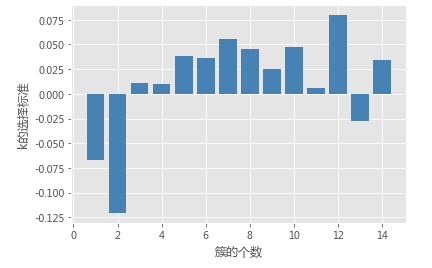
# 使用间隙统计量选择最佳的K值
gap_statistic(X, B = 20, K=range(1, 16))
# 将球员数据集聚为3类
kmeans = KMeans(n_clusters = 3)
kmeans.fit(X)
# 将聚类结果标签插入到数据集players中
players['cluster'] = kmeans.labels_
# 构建空列表,用于存储三个簇的簇中心
centers = []
for i in players.cluster.unique():
centers.append(players.ix[players.cluster == i,['得分','罚球命中率','命中率','三分命中率']].mean())
# 将列表转换为数组,便于后面的索引取数
centers = np.array(centers)
# 绘制散点图
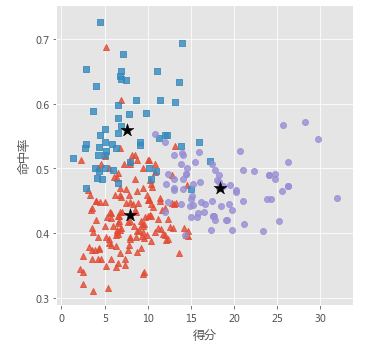
sns.lmplot(x = '得分', y = '命中率', hue = 'cluster', data = players, markers = ['^','s','o'],
fit_reg = False, scatter_kws = {'alpha':0.8}, legend = False)
# 添加簇中心
plt.scatter(centers[:,0], centers[:,2], c='k', marker = '*', s = 180)
plt.xlabel('得分')
plt.ylabel('命中率')
# 图形显示
plt.show()
# 雷达图
# 调用模型计算出来的簇中心
centers_std = kmeans.cluster_centers_
# 设置填充型雷达图
radar_chart = pygal.Radar(fill = True)
# 添加雷达图各顶点的名称
radar_chart.x_labels = ['得分','罚球命中率','命中率','三分命中率']
# 绘制雷达图代表三个簇中心的指标值
radar_chart.add('C1', centers_std[0])
radar_chart.add('C2', centers_std[1])
radar_chart.add('C3', centers_std[2])
# 保存图像
radar_chart.render_to_file('E:\radar_chart01.svg')