1. Gradient
-
我们需要观察数据的变化程度,于是导数就出现了,但是有些函数中包含多个变量,就存在这针对于每个变量的导数,也就是偏导数。(插图)
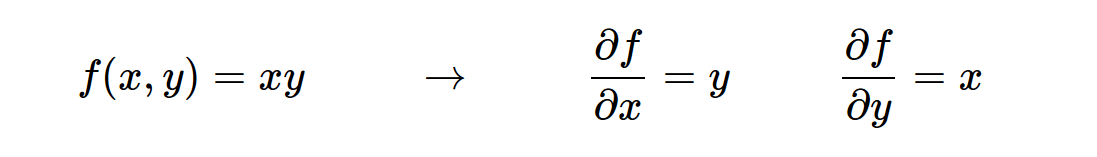
-
梯度就是偏导数的向量,然后可能是以向量的形式,存储着多个变量的偏导数,合在一起就是梯度。(插图)

-
对于一些特殊的函数的梯度,需要注意,比如
Max,它是以数据大的一方为偏导数为1,然后乘以后面传来的值,如果小的一方,偏导数为0乘以后面传来的值,得到的结果自然为0了.
2. Chain rule
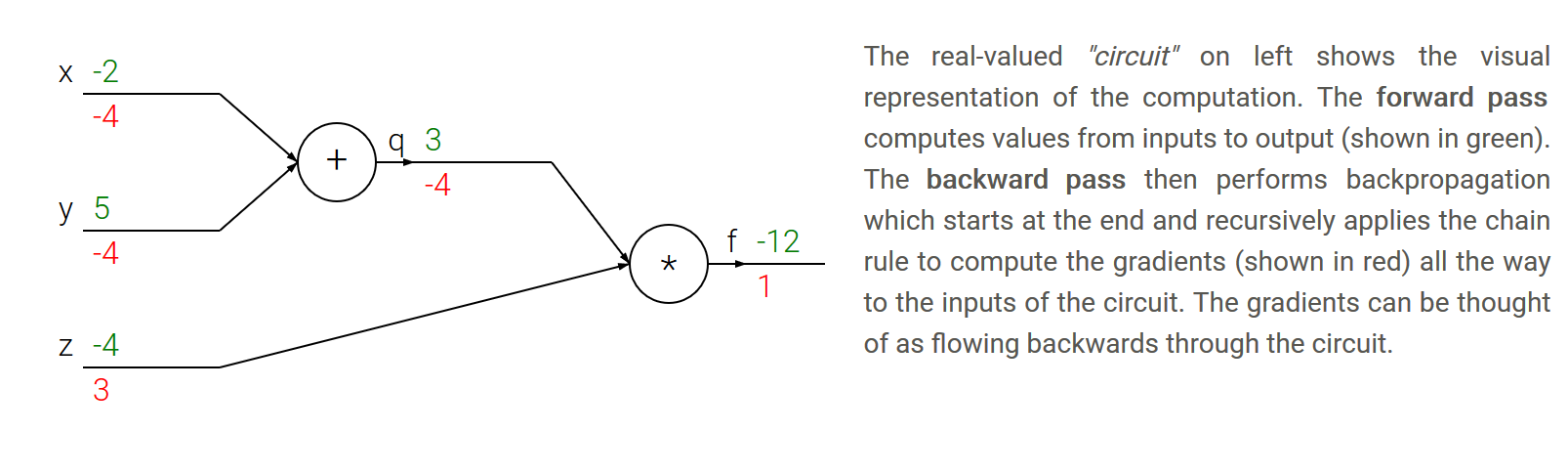
- 链式法则: 链式法则告诉我们,把这些梯度表达式连在一起的正确方法是乘法(插图)
3. Backpropagation
- 直白的讲,首先我们进行前向传播,然后就可以进行反向传播了,第一步是接收从后方传来的梯度,第二步是计算自己结点上的梯度,二者进行相乘就得到了当前结点上的偏导数。
- 一个例子,插图讲解。
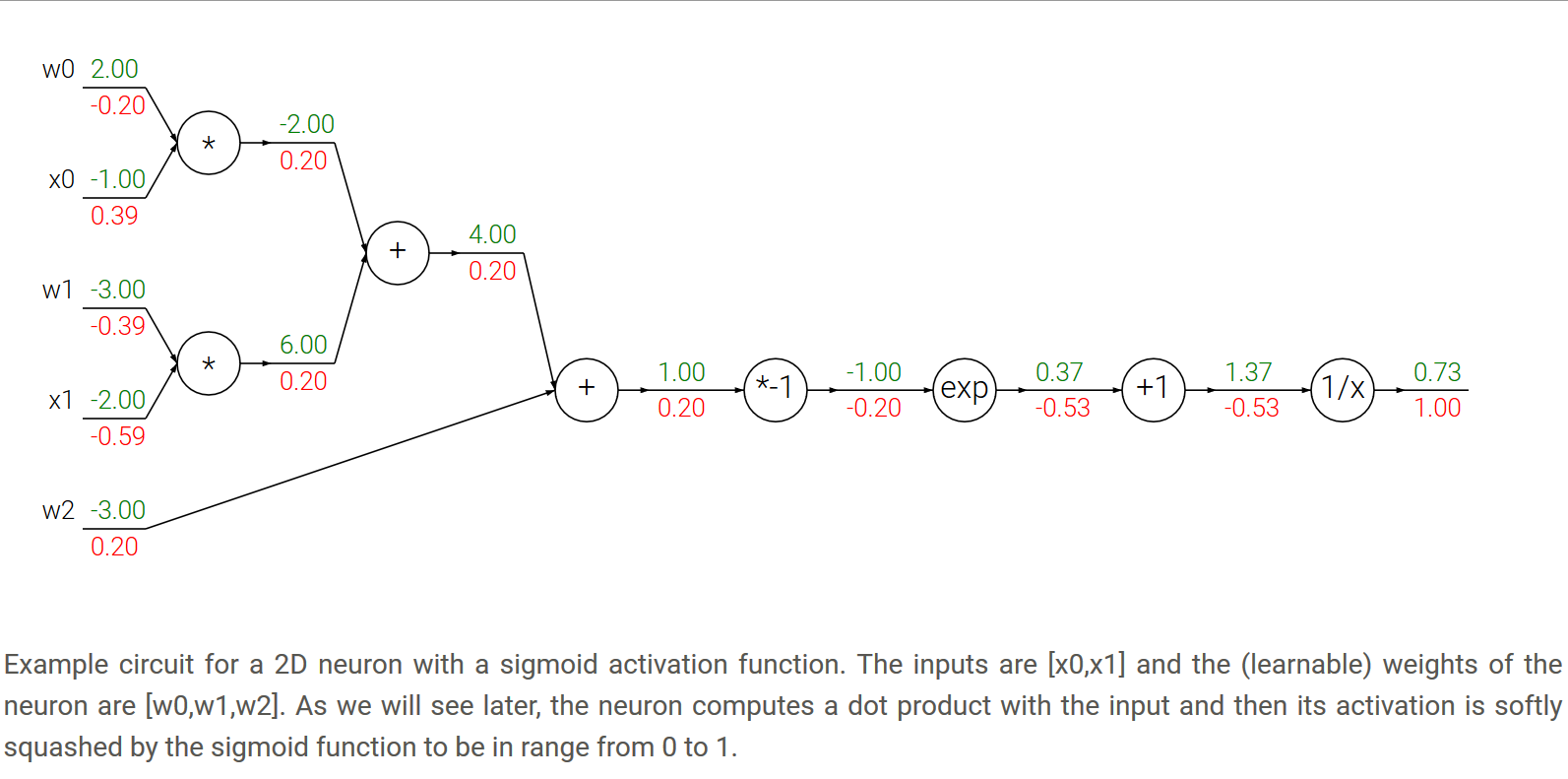
4. Patterns in backward flow
- add gate: 加法的梯度后面传来的值,与当前值直接乘以1,得到结果,也就是说,经过加法门,后面传来的值与从该门往前传的值不变。
- max gate: 这个比较特殊,值到的一方变量该结点上的梯度为1,小的一方梯度为0,然后最后的结果就是分别乘以后面传来的值,得到最终往前传的梯度,也就是该结点的梯度。
- multiply gate: 这个比较容易理解,当前结点的梯度就像普通的函数分别求偏导数即可,然后分别与后面传来的值相乘,便得到各自的最终梯度。
5. Gradients for vectorized operations
- simple case
# forward pass
W = np.random.randn(5, 10)
X = np.random.randn(10, 3)
D = W.dot(X)
# now suppose we had the gradient on D from above in the circuit
dD = np.random.randn(*D.shape) # same shape as D
dW = dD.dot(X.T) #.T gives the transpose of the matrix
dX = W.T.dot(dD)
- 解释矩阵求偏导,简单来看就是,Y的shape即尺寸大小,反向传播从后方传来一个和Y一样的shape的偏导数,然后如果要求Y对于W的偏导,那么直接是传来的shape偏导数,点积于X的转置;而对于求Y对于X的偏导,就是W的转置点积于传来的shape的偏导数。
- Y = W * X
- related document on taking matrix/vector derivatives
- 线性求偏导