神经网络与深度学习（5）：梯度消失问题

本文总结自《Neural Networks and Deep Learning》第5章的内容。 

 

问题引入

随着隐藏层数目的增加，分类准确率反而下降了。为什么？

 

消失的梯度问题（The vanishing gradient problem）

先看一组试验数据，当神经网络在训练过程中, 随epoch增加时各隐藏层的学习率变化。

两个隐藏层：[784,30,30,10]

 三个隐藏层：[784,30,30,30,10]

 四个隐藏层：[784,30,30,30,30,10]

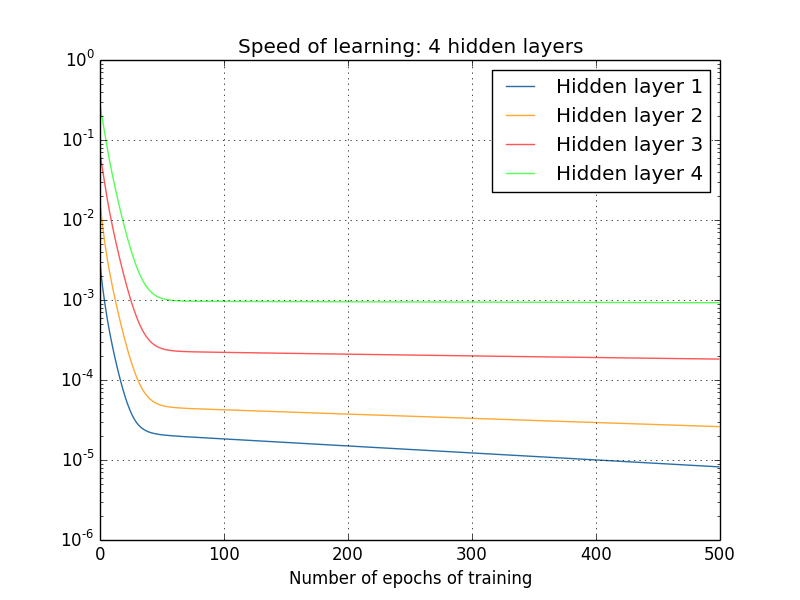
可以看到：前面的隐藏层的学习速度要低于后面的隐藏层。

这种现象普遍存在于神经网络之中， 叫做消失的梯度问题（vanishing gradient problem）。
另外一种情况是内层的梯度被外层大很多，叫做激增的梯度问题（exploding gradient problem）。

更加一般地说，在深度神经网络中的梯度是不稳定的，在前面的层中或会消失，或会激增。这种不稳定性才是深度神经网络中基于梯度学习的根本问题。

 

产生消失的梯度问题的原因

先看一个极简单的深度神经网络：每一层都只有一个单一的神经元。如下图：

代价函数C对偏置b₁的偏导数的结果计算如下：

先看一下sigmoid 函数导数的图像：

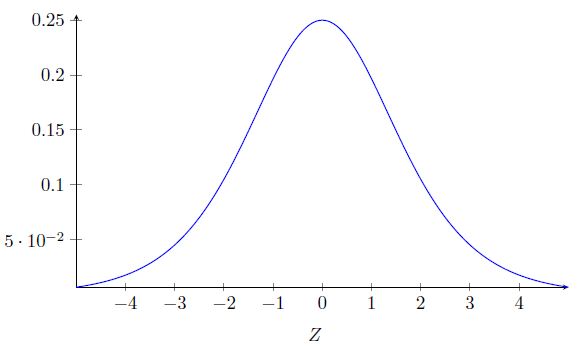
该导数在σ′(0) = 1/4时达到最高。现在，如果我们使用标准方法来初始化网络中的权重，那么会使用一个均值为0 标准差为1 的高斯分布。因此所有的权重通常会满足|w_j|<1。从而有w_jσ′(z_j) < 1/4。

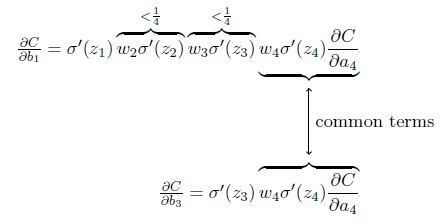
这其实就是消失的梯度出现的本质原因了。

 

可以考虑将权重初始化大一点的值，但这可能又会造成激增的梯度问题。

根本的问题其实并非是消失的梯度问题或者激增的梯度问题，而是在前面的层上的梯度是来自后面的层上项的乘积。所以神经网络非常不稳定。唯一可能的情况是以上的连续乘积刚好平衡大约等于1，但是这种几率非常小。

所以只要是sigmoid函数的神经网络都会造成梯度更新的时候极其不稳定，产生梯度消失或者激增问题。

 

解决梯度消失问题

使用ReLU。

使用ReL 函数时：gradient = 0 (if x < 0), gradient = 1 (x > 0)。不会产生梯度消失问题。