Z-score

最近处理数据时，经常用到Z-score处理方法，所以把自己了解到的知识汇集在此，对自己也是个提升，希望对别人也有所帮助。

（1）Z-score定义

     由于Z-score的数据分布满足“正态分布”(N(0,1))，而“正态分布”又被称为“Z-分布”，所以该方法被称为“Z-score”。

     Z-score是用于做数据规范化处理的一种方法。

     Z-score又称：零-均值规范化、standardscore、Z-value。

（2）Z-score公式

     Z-score的计算公式如下：

          (注：本图转载自wikipedia)
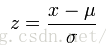
     其中x是原始数据，u是全部数据的均值，分母为标准方差。

（3）Z-score分布

     Z-score的分布如下图所示：

（注：本图转载自wikipedia）

（4）Z-score物理意义

     Z-score表示原始数据偏离均值的距离长短，而该距离度量的标准是标准方差。

     Z-score大于零表示该数据大于均值。

     Z-score小于零表示该数据小于均值。

     Z-score等于零表示该数据等于均值。

     Z-score等于“1”表示该数据比均值大一个标准方差。

     Z-score等于“-1”表示该数据比均值小一个标准方差。

     如果统计数据量足够多，Z-score数据分布满足，68%的数据分布在“-1”与“1”之间，95%的数据分布在“-2”与“2”之间，99%的数据分布在“-3”与“3之间”。可以通过此对你的数据做一定的验证。相见上面的Z-score数据分布图。

（5）Z-score应用

     Z-score可用于数据分布过于凌乱，无法判断最大值与最小值，或者数据中存在过多的奇异点，可以用Z-score方法对数据做规范化处理。

     其实Z-score也是一种数据归一化处理的一种方法。

 

 

转自：http://blog.sina.com.cn/s/blog_a89e19440101eeuo.html

 

本文参考如下链接：

http://en.wikipedia.org/wiki/Standard_score

http://stattrek.com/statistics/dictionary.aspx?definition=z_score