楔子
现在网络的安全性已经变得越来越重要,各位程序员在开发过程中或多或少都会遇到公钥、私钥、加密、签名等一些相关名词。这些概念比较杂乱,容易混淆,下面就来梳理一下这部分的内容。
对称加密
在重要的信息的传递过程中,人们总是希望信息不会被偷看、不会被篡改,伪造等。为了达到这个要求人们一直在不断努力着。
电报加密使用的密码本,就是初代网络安全所使用的加密方式,用法为:发信时将内容翻译为密文发出,收到电报的一方,使用相同的密码本才能解密出正确的信息,否则看到的就是一堆乱码。
这种传统的加密方式就叫做对称加密。
而对称加密所使用的算法包括:DES、3DES、AES、DESX、Blowfish、RC4、RC5、RC6,这些算法就可以看成密钥、或者理解为上面的密码本。这些算法也可以称为: "对称加密算法"或者"传统加密算法",一方使用算法进行加密,然后另一方使用相同的算法进行解密。
我们以《福尔摩斯探案集之跳舞的小人》一案中出现的小人为例
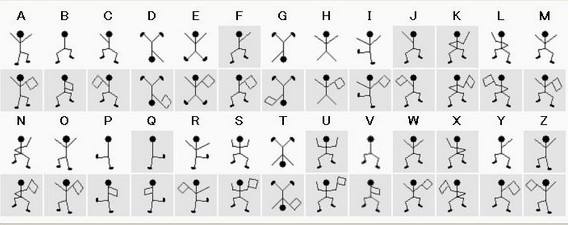
我们看到每一个小人都代表一个英文字符,至于小人手中的旗子则是用来分隔单词的、也就是表示一个单词的边界。传递信息的时候,将信息用小人来代替,然后另一方看到小人的时候,再将出现的小人解析成信息。顺便一提,剧中的女主是黑帮首领的女儿,犯人就是使用这些小人来向女主传递信息,威胁她回去。
这些小人和英文字符之间的对应关系就相当于密钥,此时就相当于一个对称加密。因为无论是发信人还是收信人,使用的是相同的密钥、即:小人代表的含义都是一样的。
但是对称算法的安全性非常依赖于密钥,泄漏密钥就意味着任何人都可以对他们发送或接收的消息解密,所以密钥的保密性对通信安全至关重要。所以福尔摩斯在解析出这些小人代表的含义之后,用这些小人发送信息将犯人引诱了出来。因此对于这种对称加密来说,密钥的安全是极其重要的。
那么对称加密有哪些优缺点呢?
优点:计算量小、加密速度快、加密效率高
缺点:1.密钥需要传递,难以确保密钥安全性。2.缺乏签名功能,即不能核对发信人身份
非对称加密
在对称加密中,密钥(也就是使用的加密算法,如上文中发电报时的密码本、小人和英文字符的对应关系)的保密性至关重要。战争时期,电报密码本需要通过人工渠道传递,这样发报双方才能放心的使用。
但如今的网络通信中,显然不可能再使用人工渠道传递密钥,只有通过网络来传递才高效快捷。这样就有了一个矛盾:密钥是用来保证网络传输安全的,这个对于网络安全至关重要的密钥又需要网络来传递给对方。
保存密钥最安全的方式就是不告诉任何人,不进行传递,但对称加密中,解密方必须要得到对应的密钥,这就又要求密钥必须进行传递,可一旦传递密钥就有丢失的风险。这个"鸡生蛋、蛋生鸡"的问题一直困扰着人们。直至出现了一种算法: 这套算法生成的密钥分为两个部分:公钥、私钥。
这个一分为二的密钥对有如下特点:
公钥和私钥是一个算法中两个不同、但内在又相关联的参数集合,同时生成,但可以独立使用。公钥加密的数据只有对应的私钥才可以解密(公钥加密后公钥也不能解密)私钥加密的数据也只有对应的公钥才可以解密。
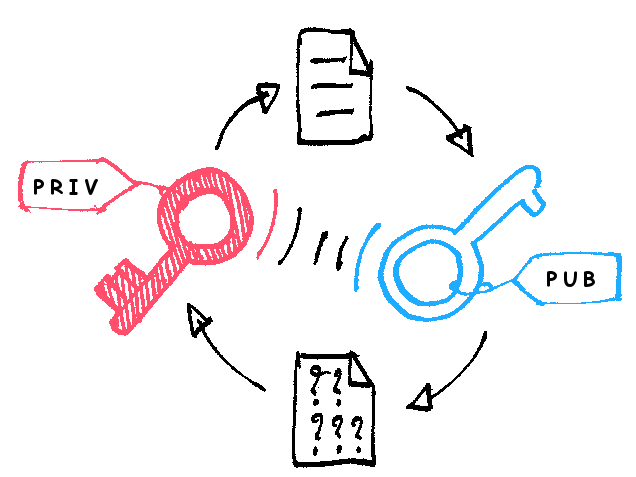
常见的非对称加密算法:RSA、DSA、ECC、Diffie-Hellman、El Gamal 等。
RSA 算法概述
对称加密的模式我们很好理解,但非对称加密算法的上述特点让我们感觉很神奇,下面让我们先来简单看看,上述这些特点在数学上是怎样实现的吧。在非对称加密算法中 RSA 是使用最广泛的一种,下面我们介绍一下 RSA。
RSA 名字的由来
RSA 算法是 1977 年由共同在麻省理工学院工作工作的 罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起提出的。RSA 就是他们三人姓氏开头字母拼在一起组成的。
RSA 加密利用了"单向函数"正向求解很简单,反向求解很复杂的特性。思想如下:
对两个质数相乘容易,而将其合数分解很难的这个特点进行的加密算法。 n=p1*p2,已知 p1、p2 求 n 简单,已知 n 求 p1、p2 困难。(m^e)%n=c,已知 m、e、n 求 c 简单,已知 e、n、c 求 m 很难。
RSA 算法的安全性基于 RSA 问题的困难性,也就是基于大整数因子分解的困难性上。这种算法非常可靠,密钥越长,它就越难破解。根据已经披露的文献,目前被破解的最长 RSA 密钥是 768 个二进制位。也就是说,长度超过 768 位的密钥,还无法破解(至少没人公开宣布)。因此可以认为,1024 位的 RSA 密钥基本安全,2048 位的密钥极其安全
非对称加密的算法比对称加密要复杂且耗时,位数越多越耗时。因此在实际使用中,一般是先用非对称加密过程传递对称加密的密钥,之后再使用对称加密来保证后续的通信,这样安全性与速度就可以达到了一个平衡,HTTPS 所使用的就是这种方式,后文会详细介绍。
使用非对称加密进行通信
有了非对称加密的公私钥对,这样通信中仅需传递公钥,甚至公钥可以开放给所有人。需要发消息给我的人使用我的公钥加密后发给我,只有我可以使用私钥解密,其他人不可能获知信息的内容。
这只是单方向的加密,双向加密怎么办呢?对方也创建一个公私钥对就可以了。
A 根据非对称加密算法生成自己的公私钥对(PUBLIC_A,PRIVATE_A);B 也根据非对称加密算法生成自己的公私钥对(PUBLIC_B,PRIVATE_B);A 和 B 可以公开的交换自己的公钥(私钥不需要发送,各自保存好即可);A 使用 B 的公钥 PUBLIC_B 加密信息,发送给 B;B 接收到消息后,使用自己保存的私钥 PRIVATE_B 解密就可以看到消息内容(这条消息即使被他人获得后也是不能解密的);同样,B 要发消息给 A 时,使用 A 的公钥 PUBLIC_A 加密发出;A 收到消息后使用自己的私钥 PRIVATE_A 解密,这样就实现了双方加密的通信。
签名
上面我们看到,有了公私钥对,似乎解决了加密通信的难题。但是实际使用中又出问题了,那就是 A 收到消息后如何确认发信人是 B 而不是第三方呢?其实也很简单,只要发消息前多进行一次使用自己的私钥加密的过程就可以了,这次使用自己私钥加密信息的步骤就叫做签名。
私钥只有自己持有,公钥和私钥存在一一对应关系,即使用公钥只能解密出对应私钥加密的信息,因此就可以用私钥的加密过程当做验证身份的手段了。其实公钥、私钥加密数据的方法与原理都相同,只是按照用途分别命名了而已。
公钥一般用来加密,私钥用来签名。
还使用上边的例子来看一下,使用了加密和签名之后的通信过程:
A 先使用自己的私钥 PRIVATE_A 对消息进行一遍加密(习惯性称作签名),再使用 B 的公钥 PUBLIC_B 加密信息,然后将加密结果发送给 B。B 接收到消息后,使用自己保存的私钥 PRIVATE_B 解密,然后使用 A 的公钥 PUBLIC_A 再解密一遍,如果能解密成功,就可以确保这条消息不是伪造的。同样,B 要发消息给 A 时先使用自己的私钥 PRIVATE_B 对消息进行一遍加密(习惯性称作签名),再使用 A 的公钥 PUBLIC_A 加密后发出。A 收到消息后使用自己的私钥 PRIVATE_A 解密,然后使用 B 的公钥 PUBLIC_B 再解密一遍,这样就实现了双方互相确认身份的加密通信。
由于非对称加密是复杂且耗时的,而且需要加密的内容越长就越耗时。在实际使用中一般经过摘要算法得到一串哈希值,然后使用私钥对哈希值进行加密。习惯性将这样对摘要使用私钥加密生成的文件叫做签名文件。
哈希值算法
生成摘要的哈希算法有如下特点:
可以将任意长度的信息与一串固定长度的字符串建立对应关系,即哈希值定长哈希值算法将任意长度映射为有限长度,难免有碰撞(即,两个不同信息算出的摘要相同)。好的哈希值算法就是能够尽量减少碰撞的几率原始信息的任何一点修改都会导致计算出的哈希值的变化,从而可以用哈希值来确保消息体的完整性。哈希值算法是单向的,即只能从原信息计算出哈希值,不能由哈希值回算得到原信息。
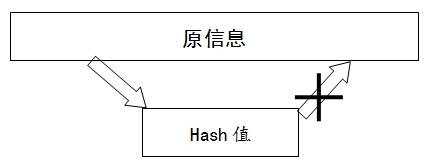
但是有的人可能见过网上有破解哈希加密的,其实它并不是反向推理,而是使用"撞库"的方式。意思就是事先对大量不同的字符串进行哈希加密,然后再将原来的字符串和生成的哈希值保存起来。然后根据用户输入的哈希值来进行检索,这就是"撞库"。不过这一般都是比较简单的哈希加密(md5),而且没有加盐。
常见算法有 MD5、SHA1、SHA256、SHA512 等。
大部分网站对用户密码保护也是利用哈希值单向性这个特点。数据库只保存用户密码的哈希值,进行登录操作时,将此次输入的密码再次计算哈希值与数据库保存的哈希值对比,对比通过则认为密码正确。这样即使数据库泄露,黑客也无法获知用户的密码。
这样就演化出了目前实际使用的签名、加密过程:
A 先使用哈希算法将要发送的消息计算出摘要,再自己的私钥 PRIVATE_A 对摘要进行签名得到签名文件,然后将原始消息和签名文件打包到一起,使用 B 的公钥 PUBLIC_B 加密信息,发送给 B。B 接收到消息后,使用自己保存的私钥 PRIVATE_B 解密,得到原始消息和一个签名文件。使用哈希算法对原始消息计算得到一个哈希值,再使用 A 的公钥 PUBLIC_A 对签名文件进行解密,得到消息的哈希值,将这两个哈希值进行对比,如果一致就可以认为这条消息是 A 发送的且未经过篡改。
公钥与证书
从上边的流程来看,似乎一切都完美了,但黑客也是绞尽脑汁的,他们还是从中找到了破绽。那就是我们对 A 的身份识别是建立在相信 PUBLIC_A 的公钥确实是 A 的,然而黑客可以轻易的发布自己的公钥宣称这是 A 的公钥来欺骗我们,那我们又怎么样区分呢?这就需要一个结构来保证了,这个机构把 A 提供的公钥和 A 的相关信息放在一起组合成一份证书,这样你从这个机构获取证书,就可以得到有权威机构背书的公钥与 A 的对应关系。
这个机构叫做 CA,发布的证书叫做 CA 证书。
证书授权中心 CA
CA 证书授权(CertificateAuthority)中心是数字证书发行的唯一机构。
CA 中心又称 CA 机构,即证书授权中心(Certificate Authority),或称证书授权机构,作为电子商务交易中受信任的第三方,承担公钥体系中公钥的合法性检验的责任。CA 中心为每个使用公开密钥的用户发放一个数字证书,数字证书的作用是证明证书中列出的用户合法拥有证书中列出的公开密钥。CA 机构的数字签名使得攻击者不能伪造和篡改证书。在 SET 交易中,CA 不仅对持卡人、商户发放证书,还要对获款的银行、网关发放证书。它负责产生、分配并管理所有参与网上交易的个体所需的数字证书,因此是安全电子交易的核心环节。
CA 证书是逐级保证安全的,最终的根证书内置在操作系统中。由操作系统来保证,这部分下文中会进行介绍。
CA证书链如下图:
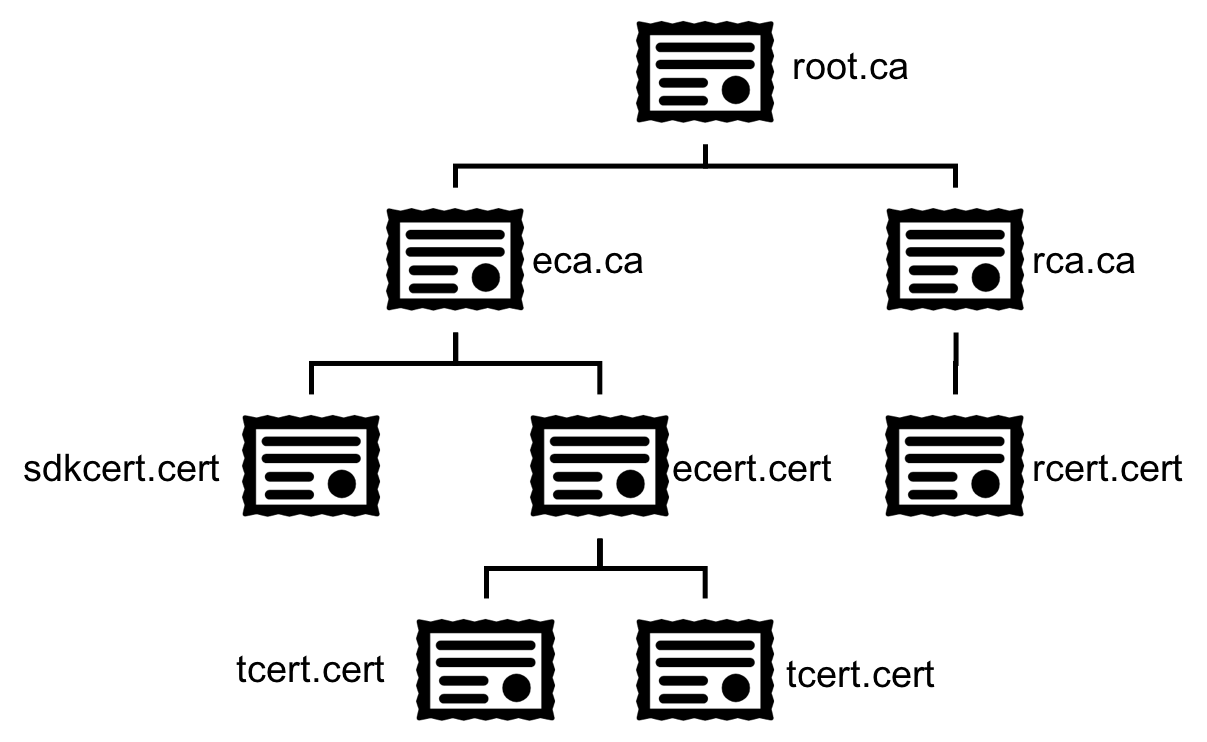
HTTPS 的安全传输过程
HTTPS 中的 S,就是 Secure(安全)的意思,这就是比 HTTP 多出的一份安全保证,浏览器验证了网站的证书后会在地址栏的左边显示绿色的锁的标志,标志该网站是安全可信任的官网。

对称加密与非对称加密的联合使用
由于非对称加密是耗时的,如果在每一次 HTTPS 的数据传输中都使用非对称加密是不合适的。实际上的做法是在第一次建立 HTTPS 连接时使用一次非对称加密传递对称加密的密钥,然后就使用对称加密来保证接下来的通信过程。
HTTPS 的通信过程如下:
浏览器发出 HTTPS 请求。服务器返回本网站的证书。浏览器基于内置在操作系统中的CA证书链对网站证书的有效性进行校验。校验通过后使用证书中的公钥加密一份对称加密的密钥信息,发送给服务端。服务端收到信息后使用自己的私钥解密信息,得到浏览器提供的用于对称加密的密钥信息。之后的通信过程就使用这个对称加密的密钥来保护。
Android 的安全启动过程(SecureBoot)
上一小节可以看到 HTTPS 的证书有效性还是要基于内置在操作系统中的 CA 根证书的。
那操作系统又是如何保证系统自身以及系统内包含的 CA 根证书不被篡改的呢?我们以 Android 来举例,因为相较于 PC 而言,手机厂商的安全性目前做的更好。
手机厂商建立了手机内部处理器与手机操作系统的绑定关系(也就是说开启 SecureBoot 功能的手机是不能刷非官方系统的),一旦刷入第三方系统后,手机则会不开机。这也是利用上文提到的公钥、私钥实现的,来具体看一下:
手机的处理器内部存在一块只能写一次数据的 OTP 区域,出厂时会将厂商的公钥写入。物理上就保证了这部分不可更改。手机操作系统固件会使用厂商的私钥进行加密。手机处理器的第一部分启动程序(这部分程序也是固化在处理器内部的不可更改)会使用 OTP 中的公钥对操作系统进行解密,解密成功才可以启动,否则立马变"砖"。
这个过程就叫做安全启动,即 SecureBoot 。实际过程中为了加快校验速度也使用了哈希值算法,但此处仅用于说明加密启动的过程,忽略了部分细节。
电脑端 Intel 处理器中其实也存在类似的机制,但一般情况下 PC 都希望能够灵活的安装系统,因此默认没有开启 Intel 芯片中的 SecureBoot 功能。