模拟退火是什么?
模拟退火来自冶金学的专有名词退火。退火是将材料加热后再经特定速率冷却,目的是增大晶粒的体积,并且减少晶格中的缺陷。材料中的原子原来会停留在使内能有局部最小值的位置,加热使能量变大,原子会离开原来位置,而随机在其他位置中移动。退火冷却时速度较慢,使得原子有较多可能可以找到内能比原先更低的位置。
模拟退火的原理也和金属退火的原理近似:我们将热力学的理论套用到统计学上,将搜寻空间内每一点想像成空气内的分子;分子的能量,就是它本身的动能;而搜寻空间内的每一点,也像空气分子一样带有“能量”,以表示该点对命题的合适程度。算法先以搜寻空间内一个任意点作起始:每一步先选择一个“邻居”,然后再计算从现有位置到达“邻居”的概率。
可以证明,模拟退火算法所得解依概率收敛到全局最优解。
演算步骤
- 初始化
生成一个可行的解作为当前解输入迭代过程,并定义一个足够大的数值作为初始温度
- 迭代
迭代过程是模拟退火算法的核心步骤,分为新解的产生和接受新解两部分
- 由一个产生函数从当前解产生一个位于解空间的新解;为便于后续的计算和接受,减少算法耗时,通常选择由当前新解经过简单地变换即可产生新解的方法,如对构成新解的全部或部分元素进行置换、互换等,注意到产生新解的变换方法决定了当前新解的邻域结构,因而对冷却进度表的选取有一定的影响。
- 计算与新解所对应的目标函数差。因为目标函数差仅由变换部分产生,所以目标函数差的计算最好按增量计算。事实表明,对大多数应用而言,这是计算目标函数差的最快方法。
- 判断新解是否被接受,判断的依据是一个接受准则,最常用的接受准则是Metropolis准则:若Δt′<0则接受S′作为新的当前解S,否则以概率exp(-Δt′/T)接受S′作为新的当前解S。
4.当新解被确定接受时,用新解代替当前解,这只需将当前解中对应于产生新解时的变换部分予以实现,同时修正目标函数值即可。此时,当前解实现了一次迭代。可在此基础上开始下一轮试验。而当新解被判定为舍弃时,则在原当前解的基础上继续下一轮试验。
注:模拟退火算法与初始值无关,算法求得的解与初始解状态S(是算法迭代的起点)无关;模拟退火算法具有渐近收敛性,已在理论上被证明是一种以概率1收敛于全局最优解的全局优化算法;模拟退火算法具有并行性。
- 停止准则
迭代过程的停止准则:温度T降至某最低值时,完成给定数量迭代中无法接受新解,停止迭代,接受当前寻找的最优解为最终解。
- 退火方案
在某个温度状态T下,当一定数量的迭代操作完成后,降低温度T,在新的温度状态下执行下一个批次的迭代操作。
- 上述内容摘自wiki百科
整个流程图如下:
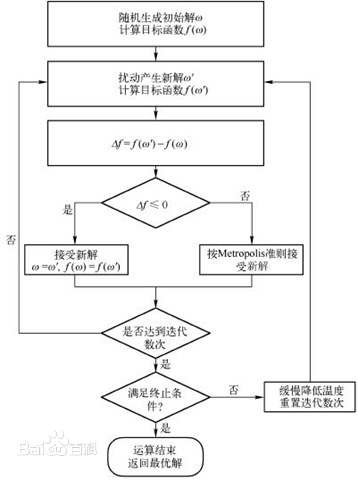
看不懂上面说的,怎么办?
没事,第一次看的时候我也看不懂,因此下面我用我的理解来讲述这个欧皇(划去)算法
和之前一样,我们通过一道题目来理解
[[JSOI2004]平衡点 ]有(n)个重物,每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞,然后系在一起。X处就是公共的绳结。假设绳子是完全弹性的(不会造成能量损失),桌子足够高(因而重物不会垂到地上),且忽略所有的摩擦。问绳结X最终平衡于何处。
注意:桌面上的洞都比绳结X小得多,所以即使某个重物特别重,绳结X也不可能穿过桌面上的洞掉下来,最多是卡在某个洞口处。
先讲一下正解的思路:
在平面上确定一个原点,将所有的力在这个平面上正交分解,从而求得所有力的合力的方向。
然后使用一个半平面切割初始的凸包,形成一个新的凸包,这样操作后凸包的面积会变小,进行多次二分,直到凸包的面积达到精度以内(即小到可以看做一个点),这时任选凸包的一个顶点就是答案。
若二分次数为(k),算法的时间复杂度为(O(kn))
至此正解结束
但这个正解很low,显示不出我们OIer真正的强大(暴力)之处,因此,我们选择模拟退火来AC这道题!
代码实现
很明显,我们先开一个结构体储存物体信息
struct Node
{
int x,y,w;
}object[2005];
//储存物体的坐标和重量
然后我们需要一个函数来计算新的系统的能量,因为根据物理学知识,一个系统的能量之和越小则越稳定
double energy(double x,double y)//计算系统新的能量
{
double r=0,dx,dy;
for(register int i=1;i<=n;++i)
{
dx=x-object[i].x;
dy=y-object[i].y;
r+=sqrt(dx*dx+dy*dy)*object[i].w;
}
return r;
}//根据物理学知识,系统能量之和越小则越稳定
接着就是多次迭代退火,逼近最优值
void sa()//simulated annealing,模拟退火
{
double t=3000;//将初始温度设为3000°C
while(t>eps)//控制精度
{
double newx=ansx+(rand()*2-RAND_MAX)*t;
double newy=ansy+(rand()*2-RAND_MAX)*t;
double neww=energy(newx,newy);
double delta=neww-answ;
if(delta<0)//新的系统能量更小(更稳定)
{
ansx=newx;
ansy=newy;
answ=neww;
}
else if(exp(-delta/t)*RAND_MAX>rand())//概率接受
{
ansx=newx;
ansy=newy;
}
t*=down;//操作完毕后降温
}
}
然后在主函数中多次退火就行了。
交代码前需要注意最重要的一步——洗脸!(笑)
模拟退火是玄学算法,因此需要多交几次才能过
至于某脸黑的tqr……
附上AC代码(调了很久才调出来的降温参数)
#include<bits/stdc++.h>
#define eps 1e-15
using namespace std;
const double down=0.994;
//降温系数,缓慢降温,关于降温参数的选取……这是个玄学问题
int n;
double ansx,ansy,answ;
//最终的答案
struct Node
{
int x,y,w;
}object[2005];
//储存物体的坐标和重量
double energy(double x,double y)//计算系统新的能量
{
double r=0,dx,dy;
for(register int i=1;i<=n;++i)
{
dx=x-object[i].x;
dy=y-object[i].y;
r+=sqrt(dx*dx+dy*dy)*object[i].w;
}
return r;
}//根据物理学知识,系统能量之和越小则越稳定
void sa()//simulated annealing,模拟退火
{
double t=3000;//将初始温度设为3000°C
while(t>eps)//控制精度
{
double newx=ansx+(rand()*2-RAND_MAX)*t;
double newy=ansy+(rand()*2-RAND_MAX)*t;
double neww=energy(newx,newy);
double delta=neww-answ;
if(delta<0)//新的系统能量更小(更稳定)
{
ansx=newx;
ansy=newy;
answ=neww;
}
else if(exp(-delta/t)*RAND_MAX>rand())//概率接受
{
ansx=newx;
ansy=newy;
}
t*=down;//操作完毕后降温
}
}
template<class T>inline void read(T &res)
{
T flag=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0';
while((c=getchar())>='0'&&c<='9')res=(res<<1)+(res<<3)+c-'0';res*=flag;
}
int main()
{
read(n);
for(register int i=1;i<=n;++i)
{
read(object[i].x);ansx+=object[i].x;
read(object[i].y);ansy+=object[i].y;
read(object[i].w);
}
ansx/=n;ansy/=n;
answ=energy(ansx,ansy);
sa();sa();sa();sa();sa();sa();
printf("%.3lf %.3lf",ansx,ansy);
return 0;
}
UPD:我发现0.994的参数,退八次火AC率很高,但不知道为什么,dalao求解qwq


