平衡树学习笔记
在学习平衡树之前,我们首先得弄懂什么是平衡树……——引言
提示:本篇约3000字,学习此内容可能需要2小时
复习部分:
先回忆一下二叉搜索树,当插入一个元素时,如果它比父节点大,就作为父节点的左儿子,否则作为父节点的右儿子。
下面这一坨就是一棵二叉搜索树
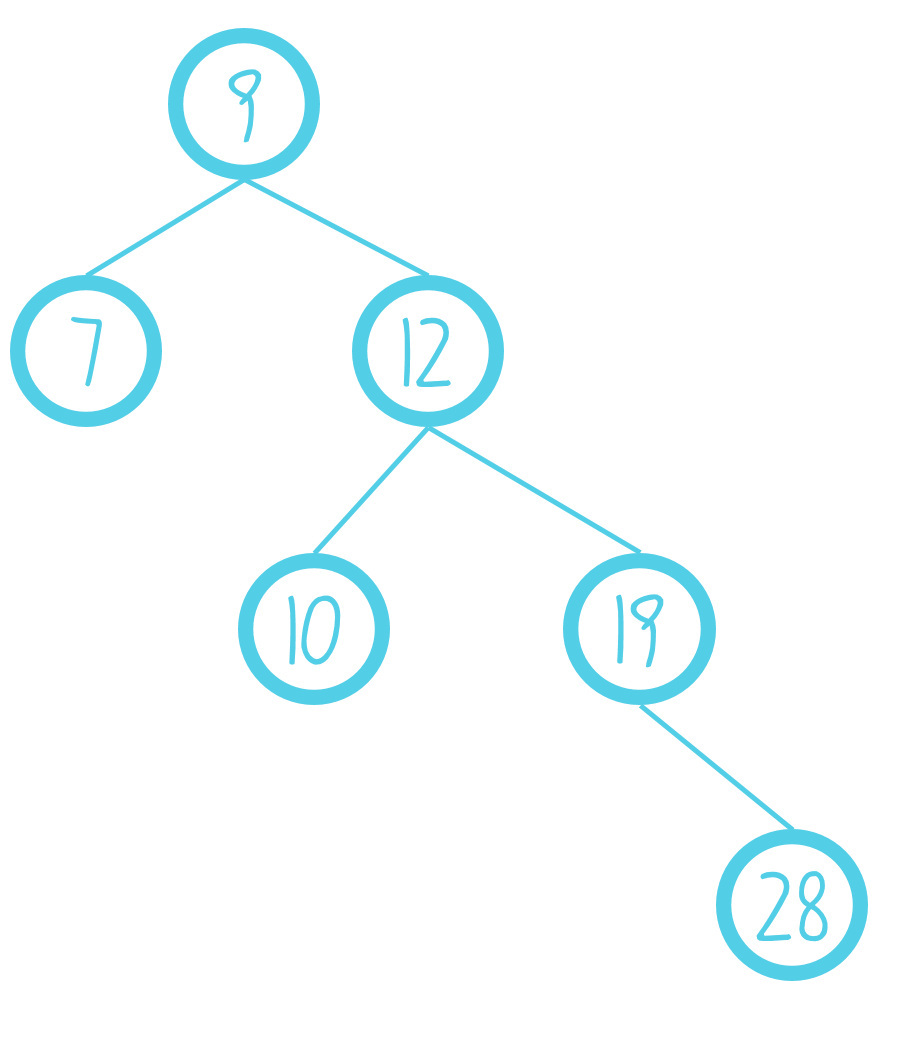
如图,当我们需要在搜索树中搜索某个元素时,只需要看它与左右儿子的大小关系,然后向左或者向右走就可以了。
二叉搜索树本来是一种很优秀的算法,搜索每一个元素的期望步数是(logN)的,因此它的时间复杂度是(O(logN))。
但是,二叉搜索树如果遇到构造数据,将会退化。如图,如果 毒瘤 出题人按顺序给出一段序列,你的二叉搜索树就会变成这个鬼样子:
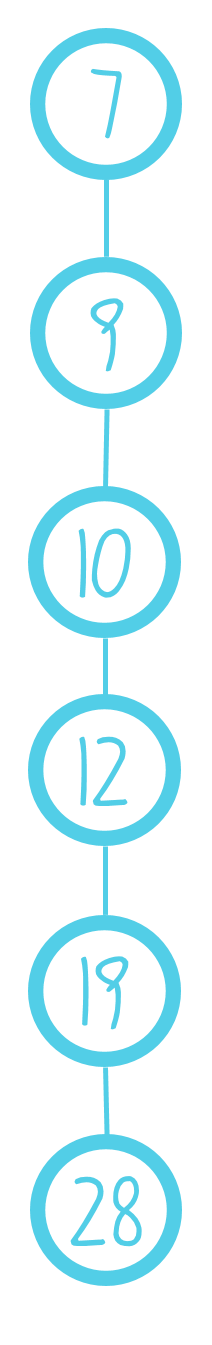
???说好的二叉搜索树呢?这TM是一条链啊!
就这样,你的二叉搜索树变成了暴力结构(查询的时间为(O(N))),还不如直接写数组爆搜。这显然是我们很讨厌的,因此,我们需要想一个办法 给出题人一点教训 优化一下二叉搜索树,让其实现自平衡。
基于这个想法,我们制造了一种数据结构——
平衡树
我们发现,二叉搜索树退化,归根到底是其一条链太长,自身不平衡所导致的时间复杂度退化。
因此,我们需要想一个办法让它平衡平衡……
设想一下,如果当某一条链太长,我们就把中间的点给拎起来,它不就平衡多了吗?
让我们模拟一下:

woc好像有点道理啊,那该怎么旋转呢?
旋转方式
通过分析,我们发现旋转有两种方式:
左旋,以及右旋
不懂没有关系,我们看一下下面的例子
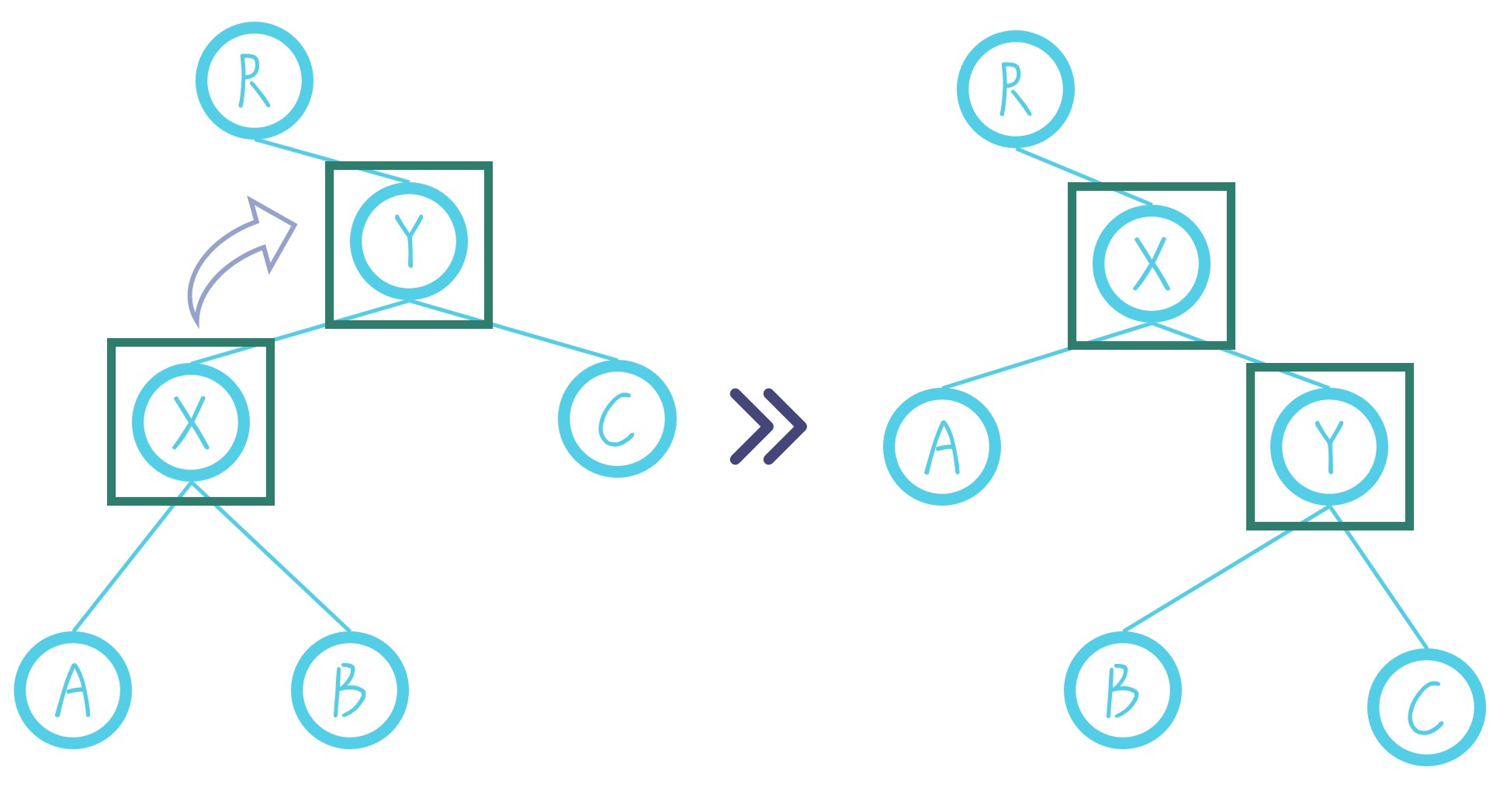
这里我们将(X)节点右旋到了(Y)节点,发生了以下的一些事情:
-
(X)的左儿子没有变化
-
(Y)变为了(X)的右儿子
-
(Y)的右儿子没有变化
-
(X)的右儿子变为了(Y)的左儿子
emmmmmmmm……这是右旋操作,左旋操作同理,各位可以自己模拟一下。
好了,我们已经知道旋转的规则了,那我们来做一道题吧:
您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
1. 插入xx数
2. 删除xx数(若有多个相同的数,因只删除一个)
3. 查询xx数的排名(定义为比当前数小的数的个数+1。若有多个相同的数,输出最小的排名)
4. 查询排名为xx的数
5. 求xx的前驱(前驱定义为小于xx,且最大的数)
6. 求xx的后继(后继定义为大于xx,且最小的数)
这就是平衡树的模板题了,怎么样,是不是很简单?(划去)

我们考虑一下怎么实现一棵平衡树
首先开一个结构体储存信息,包含节点的数值,父亲节点是谁,左右儿子,它儿子的数量以及这个元素的个数(重复次数)
#define lson ch[0]
#define rson ch[1]
struct Node
{
int v,fa,ch[2],num_son,cnt;
//节点值,父节点,左右儿子,儿子数量,重复次数
}t[100005<<3];
使树平衡的方法是对一个节点进行左旋/右旋(下图为右旋)

之前我们已经讲过下面这段话:
我们将(X)节点右旋到了(Y)节点,发生了以下的一些事情:
(X)的左儿子没有变化
(Y)变为了(X)的右儿子
(Y)的右儿子没有变化
(X)的右儿子变为了(Y)的左儿子
因为左旋和右旋的旋转方式是相反的,因此我们可以考虑只写一个函数,自动选择实现哪一种操作
自然地,写一个(identify)函数来确定一个节点与其父节点的关系,这样就可以做到自动判断该左旋还是右旋
int Identify(int x)//确定与父节点的关系
{
return t[t[x].fa].lson==x?0:1;
//其父亲的左儿子是不是自己,可以判断自己是不是左儿子
}
判断完左旋右旋后,该处理节点了。大家应该还记得一个位运算的技巧吧?
101^001=100(5^1=4)
1100^0001=1101(8^1=9)
……
多推几个式子,可以发现——奇数xor1的值为它减一,偶数xor1的值为它加一
因此,对于任何一个节点,将它的值异或1就可以求出它父亲的另一个子节点的编号(举个例子,它是右儿子的话,我们只需要将它异或1就可以求出左儿子的编号)。配合我们写好的自动判断左右儿子的函数,我们就可以做到自动判断旋转方式(左旋/右旋),自动操作。
下面是旋转的代码(无法理解的话可以先将k看为1,即右旋操作来理解,左旋完全相反)
void Rotate(int x)
{
int y=t[x].fa;//y是x原来的父亲
int z=t[y].fa;//z是x原来的爷爷
int k=Identify(x);//自己是左还是右儿子(下面的注释以右旋,即k=0为例)
t[z].ch[Identify(y)]=x;//这个节点原来的爷爷的儿子是自己
t[x].fa=z;//将这个节点的父亲设为原来自己的爷爷
//上面两步即取代父亲的位置
t[y].ch[k]=t[x].ch[k^1];//它的右儿子变为父亲的左儿子
t[t[x].ch[k^1]].fa=y;//它左儿子的父亲是它右儿子的父亲,即统一父亲
t[x].ch[k^1]=y;//它的右儿子是自己的父亲
t[y].fa=x;//它原来的父亲变为了儿子
Update(y);
Update(x);//每次操作后需要维护
}
(这一段比较复杂,建议将上面的动图与注释结合在一起看。其实这段函数的本质就是实现了一次旋转,使用位运算达到了自动判断左右旋,然后进行相反的操作罢了)
需要注意的是,每次操作后,都需要维护节点儿子数量的信息,否则会出错,也就是上面函数里的Update
这个非常好实现,相加维护一下就好了
void Update(int x)//维护儿子数量
{
t[x].num_son=t[t[x].lson].num_son+t[t[x].rson].num_son+t[x].cnt;
}
接下来,是伸展(Splay)操作,即一些博客中所说的“上旋”操作
上旋也有两种方式:一种是右旋两次(下图上部分);另一种是先左旋一次再右旋一次(下图下部分)
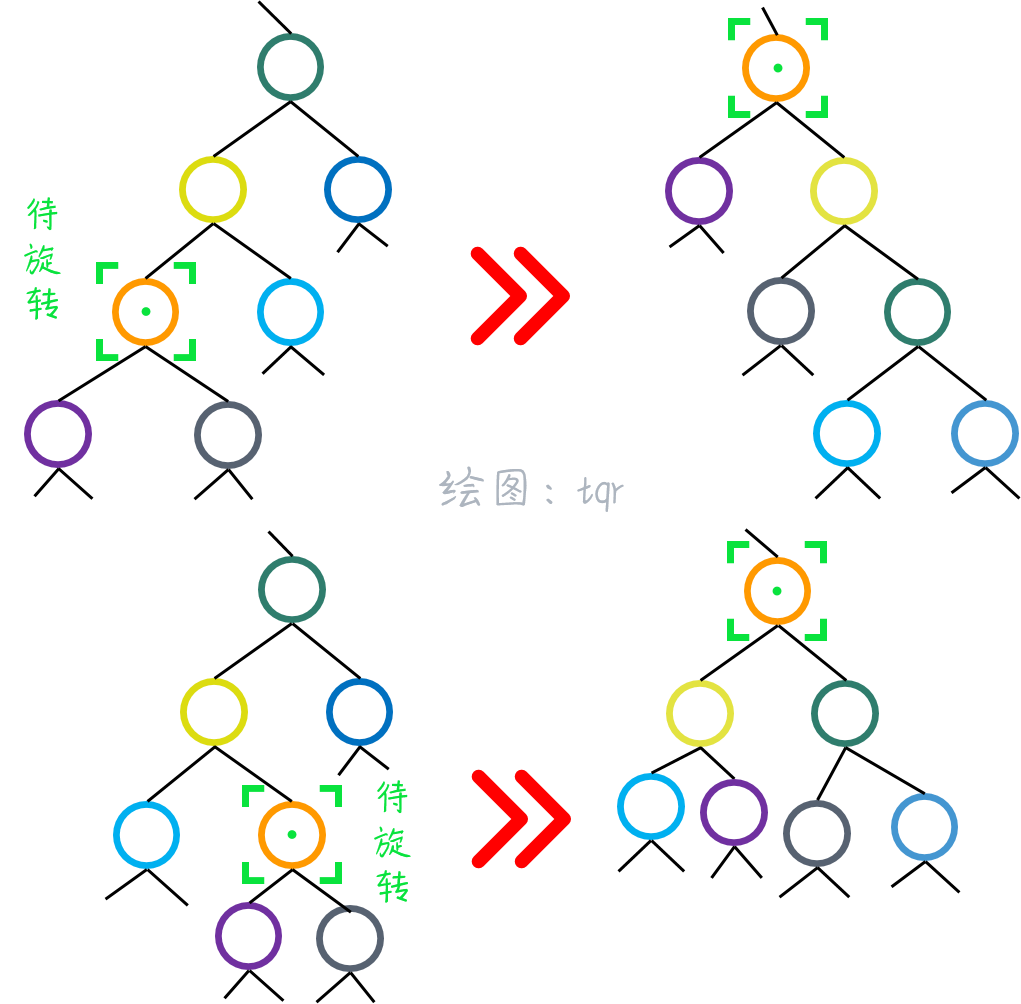
判断一下,然后右旋就可以了
void Splay(int x,int goal)//把x节点旋转到某个位置
{
while(t[x].fa!=goal)//如果还没达到目的
{
int y=t[x].fa;
int z=t[y].fa;
if(z!=goal)//如果它目标不是它的爷爷节点
(t[y].lson==x)^(t[z].lson==y)?Rotate(x):Rotate(y);
Rotate(x);
}
if(!goal) root=x;
}
此外,我们还需要完成一些题目所需要的操作。
对于插入一个节点,我们需要判断它应该被插入到哪里,以及这个数字是否存在过。如果存在过,我们只需要将这个数字的计数器+1;而如果是一个新的元素,就需要更新这个节点的诸多信息,最后Splay一下。
void Insert(int x)//插入一个节点x
{
int u=root,fa=0;
while(u&&t[u].v!=x)
{
fa=u;
u=t[u].ch[x>t[u].v];
}
if(u) ++t[u].cnt;//如果已经有这个数字了,计数+1
else//如果不存在这个数字,就加入新的节点
{
u=++tot;
if(fa) t[fa].ch[x>t[fa].v]=u;
t[tot].lson=0;
t[tot].rson=0;
t[tot].fa=fa;
t[tot].v=x;
t[tot].cnt=1;
t[tot].num_son=1;
}
Splay(u,0);
}
查询排名,前驱后继以及删除操作就比较简单,大家可以合着代码理解一下
void Find(int x)//查询x的排名
{
int u=root;
if(!u) return;//不存在节点,无法查找排名
while(t[u].ch[x>t[u].v]&&x!=t[u].v)
u=t[u].ch[x>t[u].v];
Splay(u,0);
}
int Next(int x,int opt)//0为前驱,1为后继
{
Find(x);
int u=root;
if((t[u].v>x&&opt)||(t[u].v<x&&!opt)) return u;
u=t[u].ch[opt];
while(t[u].ch[opt^1]) u=t[u].ch[opt^1];
return u;
}
void Delete(int x)
{
int last=Next(x,0);//x的前驱
int next=Next(x,1);//x的后继
Splay(last,0);Splay(next,last);
int del=t[next].lson;
if(t[del].cnt>1)
{
--t[del].cnt;//存在多个的数字被删去,计数-1
Splay(del,0);
}
else t[next].lson=0;//清除节点
}
int Kth(int x)//查询第k名是哪个数
{
int u=root;
if(t[u].num_son<x) return false;//没有这么多数
while(1)
{
int y=t[u].lson;
if(x>t[y].num_son+t[u].cnt)//在排名为u的数的后面
{
x-=t[y].num_son+t[u].cnt;//减去那么多
u=t[u].rson;//在右子树中找
}
else if(t[y].num_son>=x) u=y;//如果y的节点多于x,在左子树中找
else return t[u].v;//找到了,返回结果
}
}
至此,一棵平衡树便实现了。
我们来总结一下一棵平衡树必要的函数(排开题目所需操作)
Update,更新操作。每一次操作完成后都需要更新节点的儿子数量,使其平衡
Identify,鉴定操作。根据一个节点父亲和它自己的关系,确定它是左儿子还是右儿子,从而确定旋转的方式
Rotate,旋转操作。通过节点的左旋(右旋),达到让树平衡,防止其时间复杂度退化为(O(N))
Splay,伸展操作。即上旋,实现两次左右旋转
最后,放出上一道题完整代码:
#include<bits/stdc++.h>
#define lson ch[0]
#define rson ch[1]
using namespace std;
int T,opt,x;
int root,tot;
struct Node
{
int v,fa,ch[2],num_son,cnt;
//节点值,父节点,左右儿子,儿子数量,重复次数
}t[100005<<3];
void Update(int x)//维护儿子数量
{
t[x].num_son=t[t[x].lson].num_son+t[t[x].rson].num_son+t[x].cnt;
}
int Identify(int x)//确定与父节点的关系
{
return t[t[x].fa].lson==x?0:1;
//其父亲的左儿子是不是自己,可以判断自己是不是左儿子
}
void Rotate(int x)
{
int y=t[x].fa;//y是x原来的父亲
int z=t[y].fa;//z是x原来的爷爷
int k=Identify(x);//自己是左还是右儿子(下面的注释以右旋,即k=0为例)
t[z].ch[Identify(y)]=x;//这个节点原来的爷爷的儿子是自己
t[x].fa=z;//将这个节点的父亲设为原来自己的爷爷
//上面两步即取代父亲的位置
t[y].ch[k]=t[x].ch[k^1];//它的右儿子变为父亲的左儿子
t[t[x].ch[k^1]].fa=y;//它左儿子的父亲是它右儿子的父亲,即统一父亲
t[x].ch[k^1]=y;//它的右儿子是自己的父亲
t[y].fa=x;//它原来的父亲变为了儿子
Update(y);
Update(x);//每次操作后需要维护
}
void Splay(int x,int goal)//把x节点旋转到某个位置
{
while(t[x].fa!=goal)//如果还没达到目的
{
int y=t[x].fa;
int z=t[y].fa;
if(z!=goal)//如果它的爷爷不是目标
(t[y].lson==x)^(t[z].lson==y)?Rotate(x):Rotate(y);
Rotate(x);
}
if(!goal) root=x;
}
void Insert(int x)//插入一个节点x
{
int u=root,fa=0;
while(u&&t[u].v!=x)
{
fa=u;
u=t[u].ch[x>t[u].v];
}
if(u) ++t[u].cnt;//如果已经有这个数字了,计数+1
else//如果不存在这个数字,就加入新的节点
{
u=++tot;
if(fa) t[fa].ch[x>t[fa].v]=u;
t[tot].lson=0;
t[tot].rson=0;
t[tot].fa=fa;
t[tot].v=x;
t[tot].cnt=1;
t[tot].num_son=1;
}
Splay(u,0);
}
void Find(int x)//查询x的排名
{
int u=root;
if(!u) return;//不存在节点,无法查找排名
while(t[u].ch[x>t[u].v]&&x!=t[u].v)
u=t[u].ch[x>t[u].v];
Splay(u,0);
}
int Next(int x,int opt)//0为前驱,1为后继
{
Find(x);
int u=root;
if((t[u].v>x&&opt)||(t[u].v<x&&!opt)) return u;
u=t[u].ch[opt];
while(t[u].ch[opt^1]) u=t[u].ch[opt^1];
return u;
}
void Delete(int x)
{
int last=Next(x,0);//x的前驱
int next=Next(x,1);//x的后继
Splay(last,0);Splay(next,last);
int del=t[next].lson;
if(t[del].cnt>1)
{
--t[del].cnt;//存在多个的数字被删去,计数-1
Splay(del,0);
}
else t[next].lson=0;//清除节点
}
int Kth(int x)//查询第k名是哪个数
{
int u=root;
if(t[u].num_son<x) return false;//没有这么多数
while(1)
{
int y=t[u].lson;
if(x>t[y].num_son+t[u].cnt)//在排名为u的数的后面
{
x-=t[y].num_son+t[u].cnt;//减去那么多
u=t[u].rson;//在右子树中找
}
else if(t[y].num_son>=x) u=y;//如果y的节点多于x,在左子树中找
else return t[u].v;//找到了,返回结果
}
}
template<class T>inline void read(T &res)
{
T flag=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0';
while((c=getchar())>='0'&&c<='9')res=(res<<1)+(res<<3)+c-'0';res*=flag;
}
int main()
{
Insert(-1234567890);
Insert(+1234567890);
read(T);
while(T--)
{
read(opt);
if(opt==1)
{
read(x);
Insert(x);
}
else if(opt==2)
{
read(x);
Delete(x);
}
else if(opt==3)
{
read(x);
Find(x);
printf("%d
",t[t[root].lson].num_son);
}
else if(opt==4)
{
read(x);
printf("%d
",Kth(x+1));
}
else if(opt==5)
{
read(x);
printf("%d
",t[Next(x,0)].v);
}
else if(opt==6)
{
read(x);
printf("%d
",t[Next(x,1)].v);
}
}
return 0;
}
放到最后,其实本题还有(STL)的解法,就像下面这样
#include <bits/stdc++.h>
using namespace std;
int main()
{
vector<int> A;
int T;
cin>>T;
while(T--)
{
int opt,x;
cin>>opt>>x;
int pos=lower_bound(A.begin(),A.end(),x)-A.begin();
switch(opt)
{
case 1:A.insert(A.begin()+pos,x);break;
case 2:A.erase(A.begin()+pos,A.begin()+pos+1);break;
case 3:cout<<pos+1<<endl;break;
case 4:cout<<A[x-1]<<endl;break;
case 5:cout<<A[pos-1]<<endl;break;
case 6:cout<<*upper_bound(A.begin(),A.end(),x)<<endl;break;
}
}
return 0;
}
缺点是,这种方法所用时间是普通平衡树的五倍,因此非常不推荐使用!(实在不行拿来骗分是可以的)
END
鸣谢:
绘图:tqr
代码:tqr
讲解:tqr
……( iny ext{我鸣谢我自己})……

