实现多个堆的合并——左偏树学习笔记

在初学OI时，我们接触了一种数据结构，叫做堆。

众所周知的，我们可以使用 (STL) 的 (priority\_queue) 来快速地实现一个堆。

[ iny ext{如图，这就是一个普通的小根堆} ]

利用 (priority\_queue) ，我们可以很方便地进行堆的添加，删除等操作。

然而，当题目需要你进行堆的合并时， (priority\_queue) 便不再那么适用了。因此我们需要学习一些新的算法——左偏树

左偏树是一种树形结构，储存了一个点的数值，左右儿子和距离（被定义为它子树中离他最近的外节点到这个节点的距离）

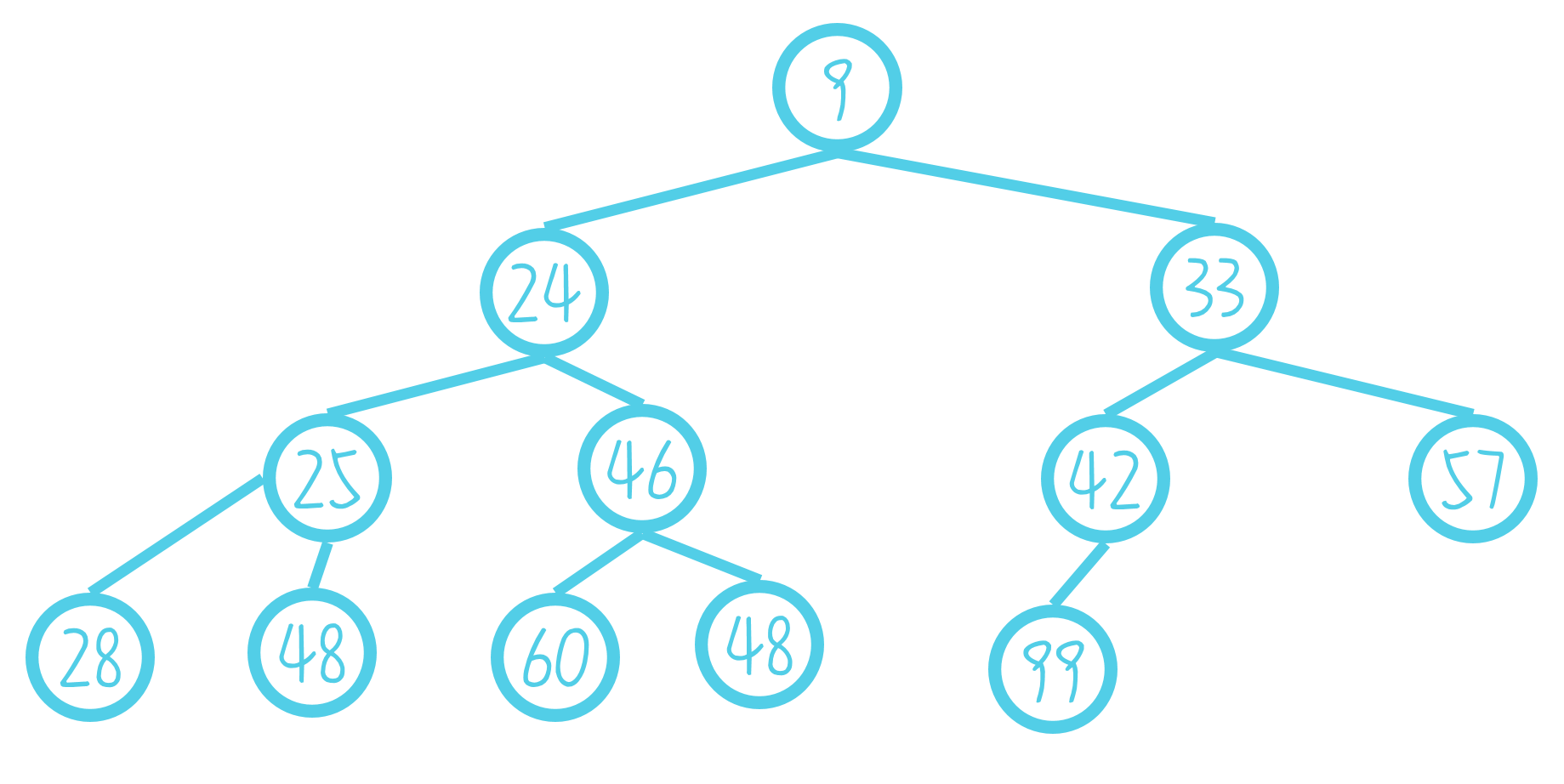
[ iny ext{如图，这是一个普通的左偏树} ]

左偏树有以下几个性质：

• 节点的权值小于等于它左右儿子的权值

• 节点的左儿子的距离不小于右儿子的距离

• 节点的距离等于右儿子的距离+1

• 一个n个节点的左偏树距离最大为 (log{(n+1)}-1)

可以看出，左偏树本身并不是平衡的，而是所有节点倒向左侧，即名字中的左偏（需要说明的是，左偏指的不是左右儿子的大小，因此如果左儿子是一个点，而右儿子是一条很长的链，那也是满足要求的左偏树）

---

概念到此为止，我们来考虑一下如何把两个堆合并

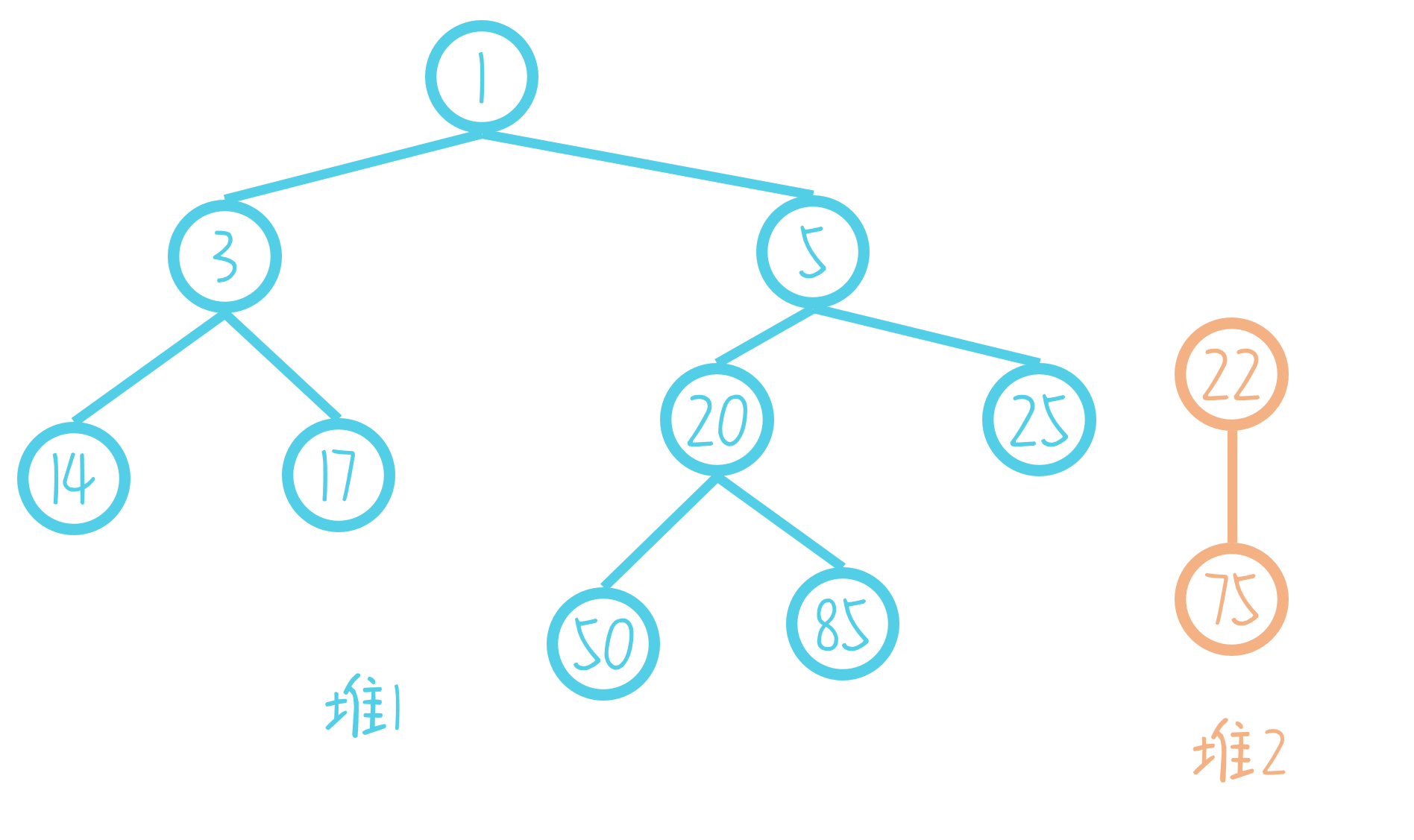
首先，我们只需要将堆2加入堆1倒数第二层的点的右儿子的左儿子，因此我们只看右儿子

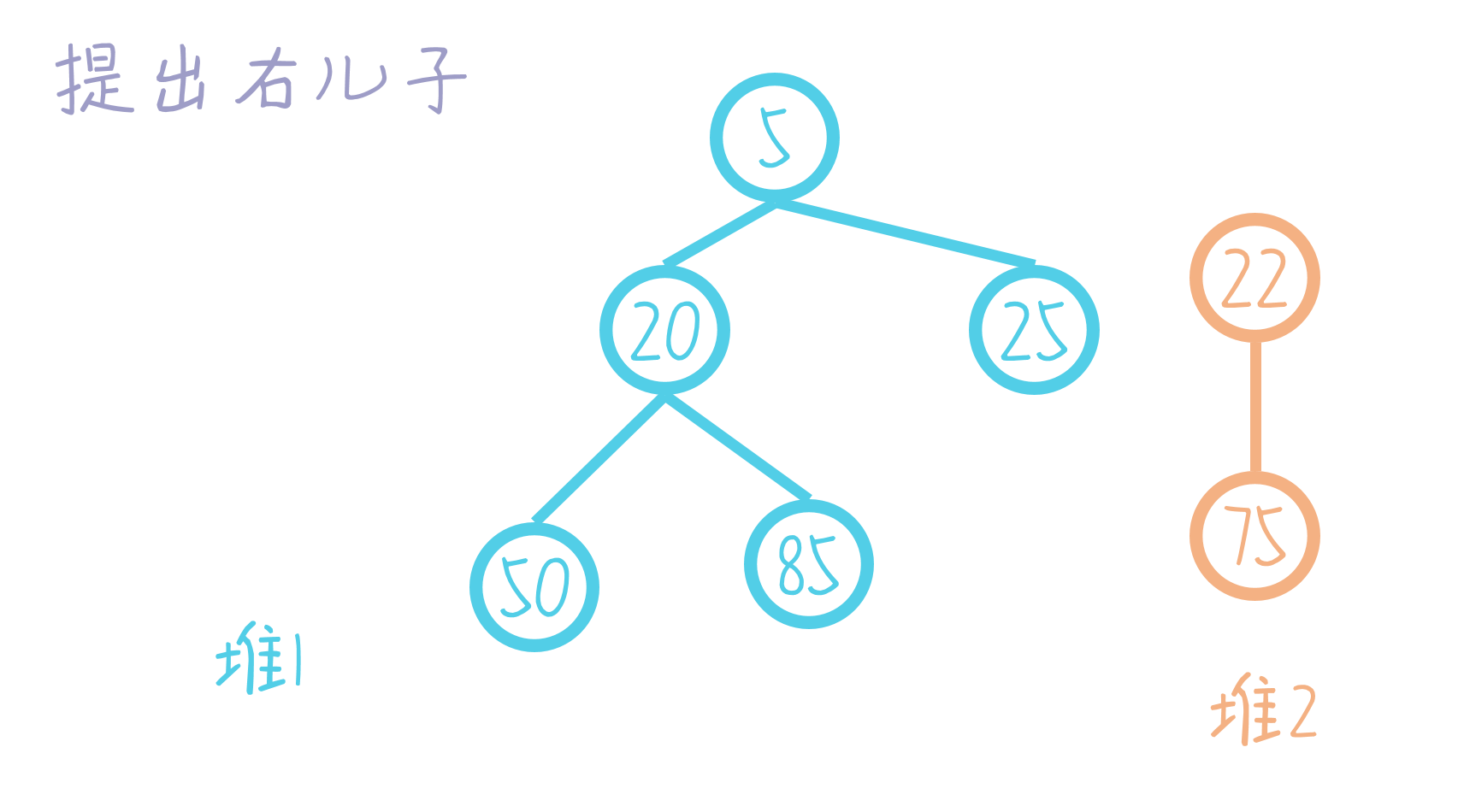
然后将堆2变为堆1的左儿子

合并

还原到初始的状态

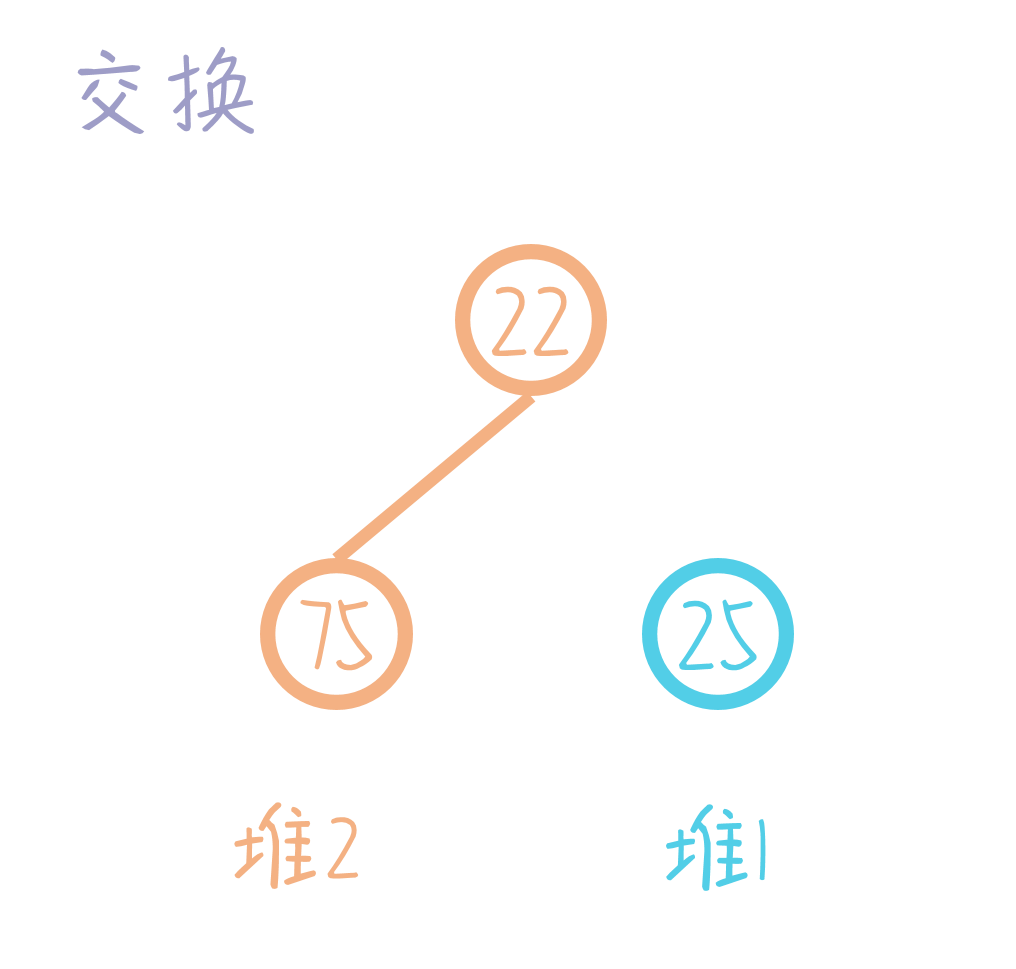
最后，由于所得堆不符合左偏树性质，交换左右儿子

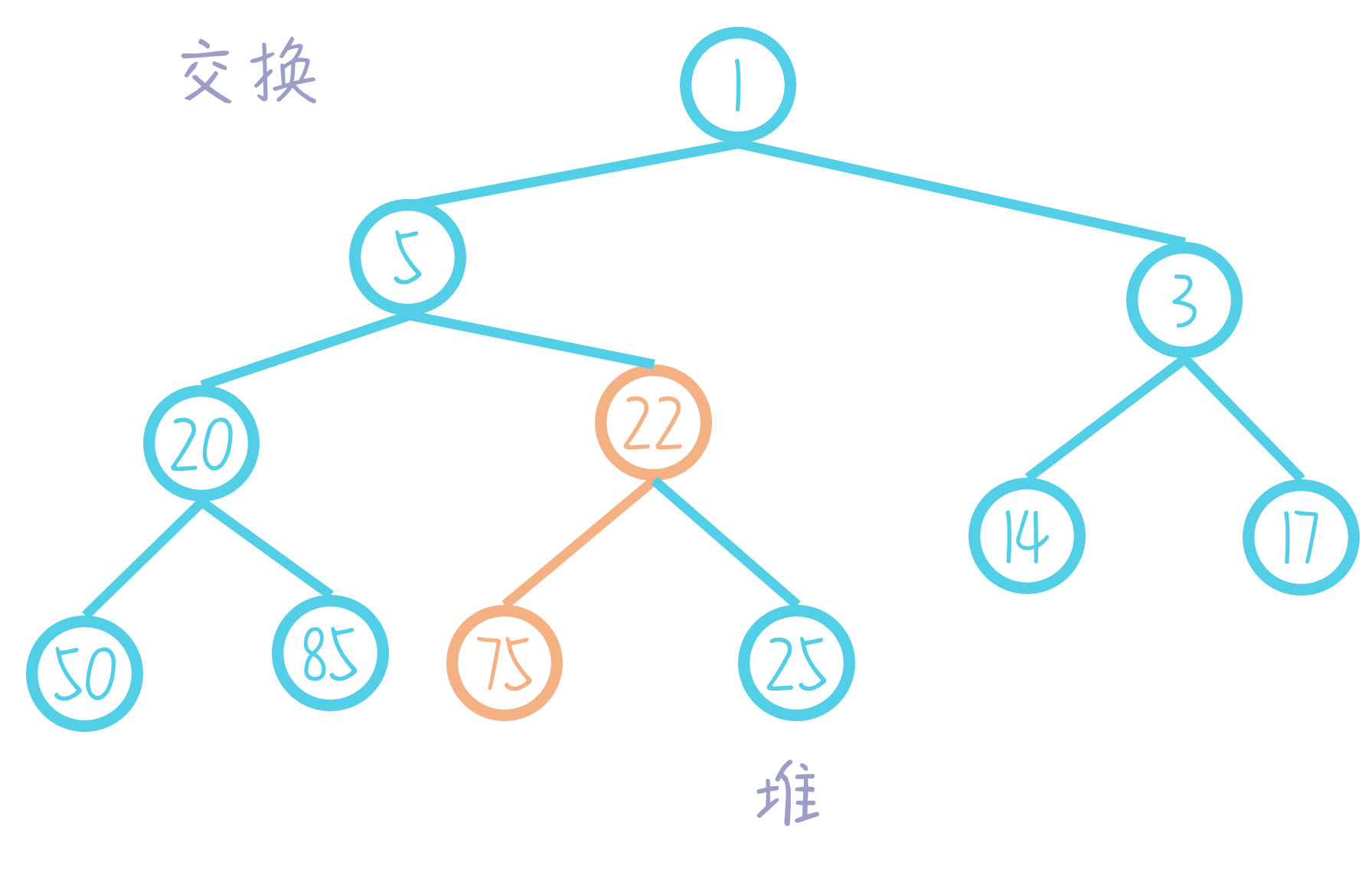
至此，我们成功地将两个堆合并在了一起

用语言口胡一下以上过程，是这样的：

1. 找到所需要的右儿子

2. 将新堆变为右儿子的左儿子

3. 找回原来的堆

4. 如果不左偏，交换左右儿子

既然原理都明白，代码就很好实现了吧

#define lson tree[x].son[0]
#define rson tree[x].son[1]

struct LeftTree
{
	int dis,v,son[2],root;
}tree[maxn];

inline void swap(int &x,int &y){x^=y^=x^=y;}

inline int merge(int x,int y)
{
	if(!x||!y) return x+y;
	if( tree[x].v>tree[y].v || (tree[x].v==tree[y].v && x>y) ) swap(x,y);//验证是否需要交换
	rson=merge(rson,y);//递归右儿子
	if(tree[lson].dis<tree[rson].dis) swap(lson,rson);//左边更浅就交换
	tree[lson].root=tree[rson].root=tree[x].root=x;
	tree[x].dis=tree[rson].dis+1;//树的深度为右儿子深度+1
	return x;
}

inline void pop(int x)
{
	tree[x].v=-1;//数值清空
	tree[lson].root=lson;
	tree[rson].root=rson;
	tree[x].root=merge(lson,rson);
}