第一次复习,4月10号,离考试还有两个周左右,来补补了。
第二次复习,4月17号,有点慌的一批了。第三次复习
第三次复习,4月22号,感觉可还行?
第四次挣扎,5月5号,感觉又有点忘了,哈哈,后天考试咯。
第一课 偏导
在数学中,一个多变量的函数的偏导数,就是它关于其中一个变量的导数而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化)。简单的来说,对某个变量求偏导的时候,其它变量看成常数。
题型一:

题型二:

注意: 还有,平方到底是什么意思。
还有,平方到底是什么意思。
题型三:

先写成F然后分步求。 如果没有明确告诉u= ,v=,就要自己找。




题型四:



第三课 全微分和偏导的应用
例一,多元函数的全微分

例二,多元复合函数的全微分

例三,已知全微分,反求未知数。

例四,多元函数求极值
①

②
③
④



例五,多元隐函数求极值

例六,多元函数求最值




例7,方向导数和梯度

求某点梯度

第七课 重积分
二重积分
二重积分的概念:二重积分是二元函数在空间上的积分,同定积分类似,是某种特定形式的和的极限。本质是求曲顶柱体体积。重积分有着广泛的应用,可以用来计算曲面的面积,平面薄片重心等。
例一,求一般格式的二重积分
只需要三步,①把未知数xy集中到后边②计算后半部分积分③计算结果代入前半部分中间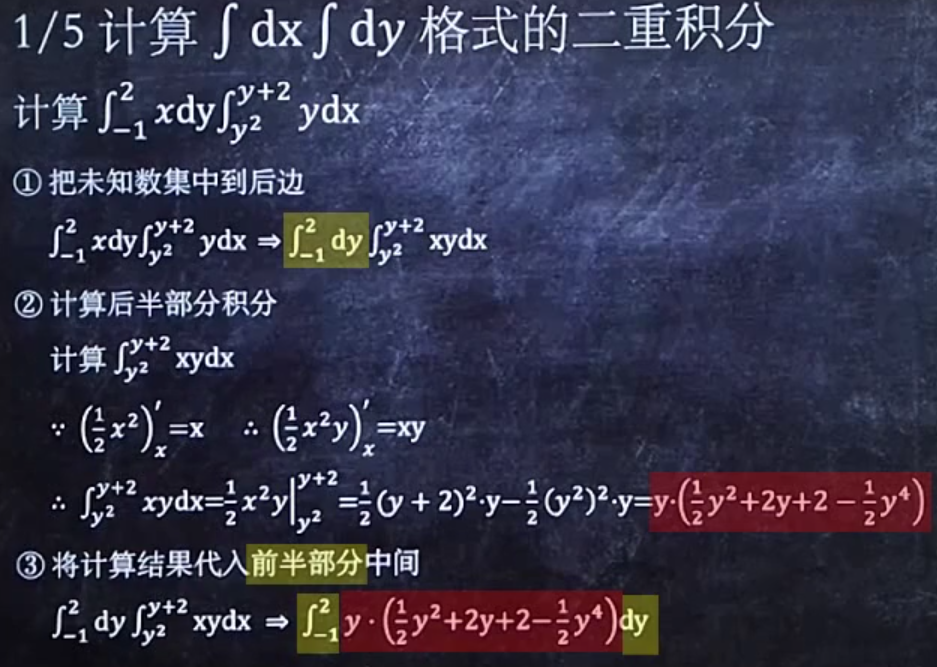
例二,交换积分次序
只需四步,①把未知数集中到后边②坐标系中画出积分区域③将x=数字,y=式子换成y=数字,x=式子,或者反过来④写出交换后的结果

再来一个题,发现这道题并不简单,想把数字和式子互换的话,还需要分割成两块区域才行。
还有一种题型,直接给出一个式子求积分,但是求原函数的时候根本无法求。

这时候交换积分次序,可能会更简单。

例三,计算另一种格式的二重积分

两种数字和式子结合的方法计算出的结果相同。
例四,积分区域和圆有关的二重积分

例记住x=rcosθ,y=rsinθ,dxdy=rdθdr。
例五,积分区域对称的二重积分
