Deep learning：五十(Deconvolution Network简单理解)

　　深度网络结构是由多个单层网络叠加而成的，而常见的单层网络按照编码解码情况可以分为下面3类：

1. 既有encoder部分也有decoder部分：比如常见的RBM系列（由RBM可构成的DBM, DBN等），autoencoder系列(以及由其扩展的sparse autoencoder, denoise autoencoder, contractive autoencoder, saturating autoencoder等)。
2. 只包含decoder部分：比如sparse coding, 和今天要讲的deconvolution network.
3. 只包含encoder部分，那就是普通的feed-forward network.

　　Deconvolution network的中文名字是反卷积网络，那么什么是反卷积呢？其概念从字面就很容易理解，假设A=B*C 表示的是：B和C的卷积是A，也就是说已知B和C，求A这一过程叫做卷积。那么如果已知A和B求C或者已知A和C求B，则这个过程就叫做反卷积了，deconvolution.

　　Deconvolution network是和convolution network(简称CNN)对应的，在CNN中，是由input image卷积feature filter得到feature map, 而在devonvolution network中，是由feature map卷积feature filter得到input image. 所以从这点看，作者强调deconvolution network是top-down是有道理的（具体可参考Zeiler的Deconvolutional networks），看下图便可知：

 　　

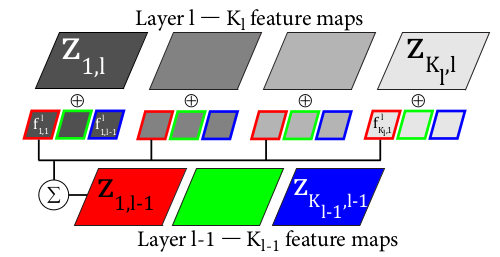
　　上图表示的是DN(deconvolution network的简称)的第一层，其输入图像是3通道的RGB图，学到的第一层特征有12个，说明每个输入通道图像都学习到了4个特征。而其中的特征图Z是由对应通道图像和特征分别卷积后再求和得到的。

　　本人感觉层次反卷积网络和层次卷积稀疏编码网络（Hierarchical Convolution Sparse Coding）非常相似，只是在Sparse Coding中对图像的分解采用的是矩阵相乘的方式，而在DN这里采用的是矩阵卷积的形式。和Sparse coding中train过程交叉优化基图像和组合系数的类似，DN中每次train时也需要交叉优化feature filter和feature map.

　　DN的train过程：

　　学习DN中第l(小写的L)层网络的特征时，需优化下面的目标函数：

 　　

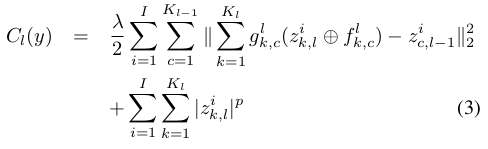
　　它是将第l层网络的输出当做第l+1层网络的输入（这和通常的deep network训练过程类似），其中的  表示第l层的特征图k和第l-1层的特征图c的连接情况，如果连接则为1,否则为0. 对上面loss函数优化的思想大致为：

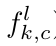1. 固定   ，优化 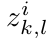  ，但是这样不能直接优化（没弄清楚原因，可参考博客下面网友的评论），因此作者引入了一个辅助变量  ，则这时的loss函数变为：

 　　

   　上式loss函数中对辅助变量  和  之间的距离进行了惩罚，因此这个辅助变量的引入是合理的，接着交替优化  和  ，直到    收敛（具体可参考文章公式细节）。

　　2. 固定  ，优化  ，直接采用梯度下降法即可。

　　DN的test过程：

　　学习到每层网络的filter后，当输入一张新图片时，可同样采用重构误差和特征图稀疏约束来优化得到本层的feature map, 比如在第一层时，需优化：

 　　

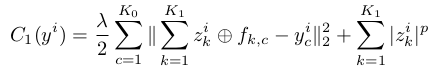
　　其中的f是在训练过程中得到的。

　　提取出图片y的DN特征后（可多层），可以用该特征进行图像的识别，也可以将该特征从上到下一层层卷积下来得到图像y’，而这个图像y’可理解为原图像y去噪后的图像。因此DN提取的特征至少有图像识别和图像去噪2个功能。

　　不难发现，如果读者对卷积稀疏编码网络熟悉的话，也就比较容易理解反卷积网络了。同理，和sparse coding一样，DA的train过程和test过程的速度都非常慢。

       读完这篇paper，不得不佩服搞数学优化的人。

　　参考资料：

　　Deconvolutional Networks, Matthew D. Zeiler, Dilip Krishnan, Graham W. Taylor and Rob Fergus.