前言:
本次主要是练习下ICA模型,关于ICA模型的理论知识可以参考前面的博文:Deep learning:三十三(ICA模型)。本次实验的内容和步骤可以是参考UFLDL上的教程:Exercise:Independent Component Analysis。本次实验完成的内容和前面的很多练习类似,即学习STL-10数据库的ICA特征。当然了,这些数据已经是以patches的形式给出,共2w个patch,8*8大小的。
实验基础:
步骤分为下面几步:
- 设置网络的参数,其中的输入样本的维数为8*8*3=192。
- 对输入的样本集进行白化,比如说ZCA白化,但是一定要将其中的参数eplison设置为0。
- 完成ICA的代价函数和其导数公式。虽然在教程Exercise:Independent Component Analysis中给出的代价函数为:
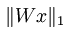
(当然了,它还必须满足权值W是正交矩阵)。
但是在UFLDL前面的一个教程Deriving gradients using the backpropagation idea中给出的代价函数却为:
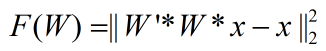
不过我感觉第2个代价函数要有道理些,并且在其教程中还给出了代价函数的偏导公式(这样实现时,可以偷懒不用推导了),只不过它给出的公式有一个小小的错误,我把正确的公式整理如下:

错误就是公式右边第一项最左边的那个应该是W,而不是它的转置W’,否则程序运行时是有矩阵维数不匹配的情况。
4. 最后就是对参数W进行迭代优化了,由于要使W满足正交性这一要求,所以不能直接像以前那样采用lbfgs算法,而是每次直接使用梯度下降法进行迭代,迭代完成后采用正交化步骤让W变成正交矩阵。只是此时文章中所说的学习率alpha是个动态变化的,是按照线性搜索来找到的。W正交性公式为:

5. 如果采用上面的代价函数和偏导公式时,用Ng给的code是跑不起来的,程序在线搜索的过程中会陷入死循环。(线搜索没有研究过,所以完全不懂)。最后在Deep Learning高质量交流群内网友”蜘蛛小侠”的提议下,将代价函数的W加一个特征稀疏性的约束,(注意此时的特征为Wx),然后把Ng的code中的迭代次数改大,比如5000,
其它程序不用更改,即可跑出结果来。
此时的代价函数为:
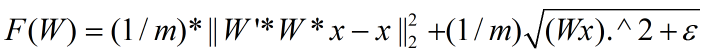
偏导为:
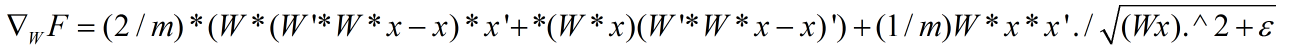
其中一定要考虑样本的个数m,否则即使通过了代价函数和其导数的验证,也不一定能通过W正交投影的验证。
实验结果:
用于训练的样本显示如下:

迭代20000次后的结果如下(因为电脑CUP不给力,跑了一天,当然了跑50000次结果会更完美,我就没时间验证了):

实验主要部分代码及注释:
ICAExercise.m:
%% CS294A/CS294W Independent Component Analysis (ICA) Exercise % Instructions % ------------ % % This file contains code that helps you get started on the % ICA exercise. In this exercise, you will need to modify % orthonormalICACost.m and a small part of this file, ICAExercise.m. %%====================================================================== %% STEP 0: Initialization % Here we initialize some parameters used for the exercise. numPatches = 20000; numFeatures = 121; imageChannels = 3; patchDim = 8; visibleSize = patchDim * patchDim * imageChannels; outputDir = '.'; % 一般情况下都将L1规则项转换成平方加一个小系数然后开根号的形式,因为L1范数在0处不可微 epsilon = 1e-6; % L1-regularisation epsilon |Wx| ~ sqrt((Wx).^2 + epsilon) %%====================================================================== %% STEP 1: Sample patches patches = load('stlSampledPatches.mat'); patches = patches.patches(:, 1:numPatches); displayColorNetwork(patches(:, 1:100)); %%====================================================================== %% STEP 2: ZCA whiten patches % In this step, we ZCA whiten the sampled patches. This is necessary for % orthonormal ICA to work. patches = patches / 255; meanPatch = mean(patches, 2); patches = bsxfun(@minus, patches, meanPatch); sigma = patches * patches'; [u, s, v] = svd(sigma); ZCAWhite = u * diag(1 ./ sqrt(diag(s))) * u'; patches = ZCAWhite * patches; %%====================================================================== %% STEP 3: ICA cost functions % Implement the cost function for orthornomal ICA (you don't have to % enforce the orthonormality constraint in the cost function) % in the function orthonormalICACost in orthonormalICACost.m. % Once you have implemented the function, check the gradient. % Use less features and smaller patches for speed % numFeatures = 5; % patches = patches(1:3, 1:5); % visibleSize = 3; % numPatches = 5; % % weightMatrix = rand(numFeatures, visibleSize); % % [cost, grad] = orthonormalICACost(weightMatrix, visibleSize, numFeatures, patches, epsilon); % % numGrad = computeNumericalGradient( @(x) orthonormalICACost(x, visibleSize, numFeatures, patches, epsilon), weightMatrix(:) ); % % Uncomment to display the numeric and analytic gradients side-by-side % % disp([numGrad grad]); % diff = norm(numGrad-grad)/norm(numGrad+grad); % fprintf('Orthonormal ICA difference: %g\n', diff); % assert(diff < 1e-7, 'Difference too large. Check your analytic gradients.'); % % fprintf('Congratulations! Your gradients seem okay.\n'); %%====================================================================== %% STEP 4: Optimization for orthonormal ICA % Optimize for the orthonormal ICA objective, enforcing the orthonormality % constraint. Code has been provided to do the gradient descent with a % backtracking line search using the orthonormalICACost function % (for more information about backtracking line search, you can read the % appendix of the exercise). % % However, you will need to write code to enforce the orthonormality % constraint by projecting weightMatrix back into the space of matrices % satisfying WW^T = I. % % Once you are done, you can run the code. 10000 iterations of gradient % descent will take around 2 hours, and only a few bases will be % completely learned within 10000 iterations. This highlights one of the % weaknesses of orthonormal ICA - it is difficult to optimize for the % objective function while enforcing the orthonormality constraint - % convergence using gradient descent and projection is very slow. weightMatrix = rand(numFeatures, visibleSize);%121*192 [cost, grad] = orthonormalICACost(weightMatrix(:), visibleSize, numFeatures, patches, epsilon); fprintf('%11s%16s%10s\n','Iteration','Cost','t'); startTime = tic(); % Initialize some parameters for the backtracking line search alpha = 0.5; t = 0.02; lastCost = 1e40; % Do 10000 iterations of gradient descent for iteration = 1:20000 grad = reshape(grad, size(weightMatrix)); newCost = Inf; linearDelta = sum(sum(grad .* grad)); % Perform the backtracking line search while 1 considerWeightMatrix = weightMatrix - alpha * grad; % -------------------- YOUR CODE HERE -------------------- % Instructions: % Write code to project considerWeightMatrix back into the space % of matrices satisfying WW^T = I. % % Once that is done, verify that your projection is correct by % using the checking code below. After you have verified your % code, comment out the checking code before running the % optimization. % Project considerWeightMatrix such that it satisfies WW^T = I % error('Fill in the code for the projection here'); considerWeightMatrix = (considerWeightMatrix*considerWeightMatrix')^(-0.5)*considerWeightMatrix; % Verify that the projection is correct temp = considerWeightMatrix * considerWeightMatrix'; temp = temp - eye(numFeatures); assert(sum(temp(:).^2) < 1e-23, 'considerWeightMatrix does not satisfy WW^T = I. Check your projection again'); % error('Projection seems okay. Comment out verification code before running optimization.'); % -------------------- YOUR CODE HERE -------------------- [newCost, newGrad] = orthonormalICACost(considerWeightMatrix(:), visibleSize, numFeatures, patches, epsilon); if newCost >= lastCost - alpha * t * linearDelta t = 0.9 * t; else break; end end lastCost = newCost; weightMatrix = considerWeightMatrix; fprintf(' %9d %14.6f %8.7g\n', iteration, newCost, t); t = 1.1 * t; cost = newCost; grad = newGrad; % Visualize the learned bases as we go along if mod(iteration, 10000) == 0 duration = toc(startTime); % Visualize the learned bases over time in different figures so % we can get a feel for the slow rate of convergence figure(floor(iteration / 10000)); displayColorNetwork(weightMatrix'); end end % Visualize the learned bases displayColorNetwork(weightMatrix');
orthonormalICACost.m:
function [cost, grad] = orthonormalICACost(theta, visibleSize, numFeatures, patches, epsilon) %orthonormalICACost - compute the cost and gradients for orthonormal ICA % (i.e. compute the cost ||Wx||_1 and its gradient) weightMatrix = reshape(theta, numFeatures, visibleSize); cost = 0; grad = zeros(numFeatures, visibleSize); % -------------------- YOUR CODE HERE -------------------- % Instructions: % Write code to compute the cost and gradient with respect to the % weights given in weightMatrix. % -------------------- YOUR CODE HERE -------------------- %% 法一: num_samples = size(patches,2); % cost = sum(sum((weightMatrix'*weightMatrix*patches-patches).^2))./num_samples+... % sum(sum(sqrt((weightMatrix*patches).^2+epsilon)))./num_samples; % grad = (2*weightMatrix*(weightMatrix'*weightMatrix*patches-patches)*patches'+... % 2*weightMatrix*patches*(weightMatrix'*weightMatrix*patches-patches)')./num_samples+... % ((weightMatrix*patches./sqrt((weightMatrix*patches).^2+epsilon))*patches')./num_samples; cost = sum(sum((weightMatrix'*weightMatrix*patches-patches).^2))./num_samples+... sum(sum(sqrt((weightMatrix*patches).^2+epsilon))); grad = (2*weightMatrix*(weightMatrix'*weightMatrix*patches-patches)*patches'+... 2*weightMatrix*patches*(weightMatrix'*weightMatrix*patches-patches)')./num_samples+... (weightMatrix*patches./sqrt((weightMatrix*patches).^2+epsilon))*patches'; grad = grad(:); end
参考资料: