Sparse coding:
本节将简单介绍下sparse coding(稀疏编码),因为sparse coding也是deep learning中一个重要的分支,同样能够提取出数据集很好的特征。本文的内容是参考斯坦福deep learning教程:Sparse Coding,Sparse Coding: Autoencoder Interpretation,对应的中文教程见稀疏编码,稀疏编码自编码表达。
在次之前,我们需要对凸优化有些了解,百度百科解释为:”凸优化“ 是指一种比较特殊的优化,是指目标函数为凸函数且由约束条件得到的定义域为凸集的优化问题,也就是说目标函数和约束条件都是”凸”的。
好了,现在开始简单介绍下sparse coding, sparse coding是将输入的样本集X分解为多个基元的线性组合,然后这些基前面的系数表示的是输入样本的特征。其分解公式表达如下:
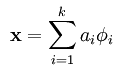
而一般情况下要求基的个数k非常大,至少要比x中元素的个数n要大,因为这样的基组合才能更容易的学到输入数据内在的结构和特征。其实在常见的PCA算法中,是可以找到一组基来分解X的,只不过那个基的数目比较小,所以可以得到分解后的系数a是可以唯一确定,而在sparse coding中,k太大,比n大很多,其分解系数a不能唯一确定。一般的做法是对系数a作一个稀疏性约束,这也就是sparse coding算法的来源。此时系统对应的代价函数(前面的博文都用损失函数表示,以后统一改用代价函数,感觉这样翻译更贴切)表达式为:
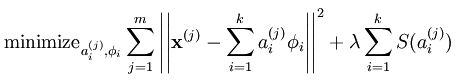
其中的第一项是重构输入数据X的代价值,第二项的S(.)为分解系数的系数惩罚,lamda是两种代价的权重,是个常量。但是这样还是有一个问题,比如说我们可以将系数a减到很小,且将每个基的值增加到很大,这样第一项的代价值基本保持不变,而第二项的稀疏惩罚依旧很小,达不到我们想要的目的——分解系数中只有少数系数远远大于0,而不是大部分系数都比0大(虽然不会大太多)。解决这个问题的通用方法是是对基集合中的值也做了一个约束,约束后的系统代价函数为:
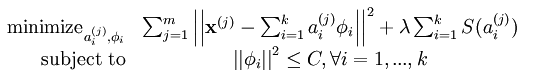
Sparse coding的概率解释:
主要是从概率的角度来解释sparse coding方法,不过这一部分的内容还真没太看明白,只能讲下自己的大概理解。如果把误差考虑进去后,输入样本X经过sparse coding分解后的表达式则如下:
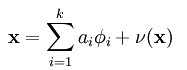
而我们的目标是找到一组基Ф,使得输入样本数据出现的概率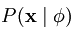 与输入样本数据的经验分布概率
与输入样本数据的经验分布概率 最相近,如果用KL距离来衡量其相似度的话,就是满足他们的KL距离最小,即下面表达式值最小:
最相近,如果用KL距离来衡量其相似度的话,就是满足他们的KL距离最小,即下面表达式值最小:

由于输入数据的经验分布函数概率是固定值,所以求上式值最小相当等价于求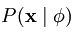 最大。
最大。
经过对参数a的先验估计和函数积分值估计等推导步骤,最后等价于求下面的能量函数值最小:

而这就很好的和sparse coding的代价函数公式给联系起来了。
到目前为止我们应该知道sparse coding的实际使用过程中速度是很慢的,因为即使我们在训练阶段已经把输入数据集的基Ф学习到了,在测试阶段时还是要通过凸优化的方法去求得其特征值(即基组合前面的系数值),所以这比一般的前向神经网络速度要慢(一般的前向算法只需用矩阵做一下乘法,然后做下加法,求个函数值等少数几步即可完成)。
Sparse coding的autoencoder解释:
首先来看看向量X的Lk规范数,其值为:![]() 由此可知,L1范数为各元素之和,L2范数为该向量到远点的欧式距离。
由此可知,L1范数为各元素之和,L2范数为该向量到远点的欧式距离。
用矩阵的形式来表达sparse coding的代价函数如下:
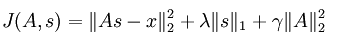
和前面所讲的一样,这里也对基值s做了稀疏性惩罚,用的是L1范数来约束,同时也防止系数矩阵A过大,对其用的是L2范数的平方来约束。但是基值处的L1范数在0点是无法求导的,所以不能用梯度下降等类似的方法来对上面的代价函数求最优参数,于是为了在0处可导,可将公式变成如下:
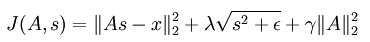
拓扑sparse coding:
拓扑sparse coding主要是模仿人体大脑皮层中相邻的神经元对能提取出某一相近的特征,因此在deep learning中我们希望学习到的特征也具有这样“拓扑秩序”的性质。如果我们随意的将特征排列成一个矩阵,则我们希望矩阵中相邻的特征是相似的。也就是把原先那些特征系数的稀疏性惩罚项L1范数更改为不同小组L1范数惩罚之和,而这些相邻小组之间是有重叠值的,因此只要重叠的那一部分值改变就意味着各自组的惩罚值也会改变,这也就体现出了类似人脑皮层的特性,因此此时系统的代价函数为:
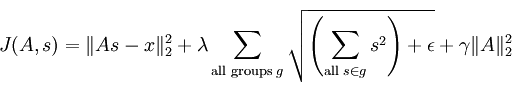
改成矩阵的形式后如下:

总结:
在实际编程时,为了写出准确无误的优化函数代码并能快速又恰到好处地收敛到最优值,可以采用下面的技巧:
- 将输入样本集分成多个小的mini-batches,这样做的好处是每次迭代时输入系统的样本数变少了,运行的时间也会变短很多,并且也提高了整体收敛速度。(暂时还没弄明白原因)。
- S的初始化值不能随机给。一般都是按照下面的方法进行:

最后,在实际优化该代价函数时步骤大致如下:
- 随机初始化A
- 重复以下步骤直至收敛
- 随机选取一个有小的mini-batches。
- 按照前面讲的方法来s。
- 根据上一步给定的A,求解能够最小化J(A,s)的s
- 根据上一步得到的s,求解能够最小化J(A,s)的A
参考资料: