前言:
现在来用PCA,PCA Whitening对自然图像进行处理。这些理论知识参考前面的博文:Deep learning:十(PCA和whitening)。而本次试验的数据,步骤,要求等参考网页:http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial 。实验数据是从自然图像中随机选取10000个12*12的patch,然后对这些patch进行99%的方差保留的PCA计算,最后对这些patch做PCA Whitening和ZCA Whitening,并进行比较。
实验环境:matlab2012a
实验过程及结果:
随机选取10000个patch,并显示其中204个patch,如下图所示:

然后对这些patch做均值为0化操作得到如下图:

对选取出的patch做PCA变换得到新的样本数据,其新样本数据的协方差矩阵如下图所示:

保留99%的方差后的PCA还原原始数据,如下所示:

PCA Whitening后的图像如下:

此时样本patch的协方差矩阵如下:
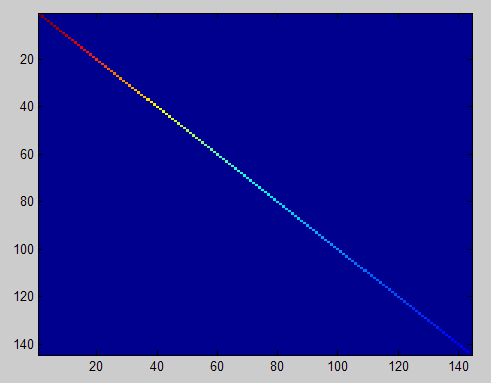
ZCA Whitening的结果如下:

实验代码及注释:
%%================================================================ %% Step 0a: Load data % Here we provide the code to load natural image data into x. % x will be a 144 * 10000 matrix, where the kth column x(:, k) corresponds to % the raw image data from the kth 12x12 image patch sampled. % You do not need to change the code below. x = sampleIMAGESRAW(); figure('name','Raw images'); randsel = randi(size(x,2),204,1); % A random selection of samples for visualization display_network(x(:,randsel));%为什么x有负数还可以显示? %%================================================================ %% Step 0b: Zero-mean the data (by row) % You can make use of the mean and repmat/bsxfun functions. % -------------------- YOUR CODE HERE -------------------- x = x-repmat(mean(x,1),size(x,1),1);%求的是每一列的均值 %x = x-repmat(mean(x,2),1,size(x,2)); %%================================================================ %% Step 1a: Implement PCA to obtain xRot % Implement PCA to obtain xRot, the matrix in which the data is expressed % with respect to the eigenbasis of sigma, which is the matrix U. % -------------------- YOUR CODE HERE -------------------- xRot = zeros(size(x)); % You need to compute this [n m] = size(x); sigma = (1.0/m)*x*x'; [u s v] = svd(sigma); xRot = u'*x; %%================================================================ %% Step 1b: Check your implementation of PCA % The covariance matrix for the data expressed with respect to the basis U % should be a diagonal matrix with non-zero entries only along the main % diagonal. We will verify this here. % Write code to compute the covariance matrix, covar. % When visualised as an image, you should see a straight line across the % diagonal (non-zero entries) against a blue background (zero entries). % -------------------- YOUR CODE HERE -------------------- covar = zeros(size(x, 1)); % You need to compute this covar = (1./m)*xRot*xRot'; % Visualise the covariance matrix. You should see a line across the % diagonal against a blue background. figure('name','Visualisation of covariance matrix'); imagesc(covar); %%================================================================ %% Step 2: Find k, the number of components to retain % Write code to determine k, the number of components to retain in order % to retain at least 99% of the variance. % -------------------- YOUR CODE HERE -------------------- k = 0; % Set k accordingly ss = diag(s); % for k=1:m % if sum(s(1:k))./sum(ss) < 0.99 % continue; % end %其中cumsum(ss)求出的是一个累积向量,也就是说ss向量值的累加值 %并且(cumsum(ss)/sum(ss))<=0.99是一个向量,值为0或者1的向量,为1表示满足那个条件 k = length(ss((cumsum(ss)/sum(ss))<=0.99)); %%================================================================ %% Step 3: Implement PCA with dimension reduction % Now that you have found k, you can reduce the dimension of the data by % discarding the remaining dimensions. In this way, you can represent the % data in k dimensions instead of the original 144, which will save you % computational time when running learning algorithms on the reduced % representation. % % Following the dimension reduction, invert the PCA transformation to produce % the matrix xHat, the dimension-reduced data with respect to the original basis. % Visualise the data and compare it to the raw data. You will observe that % there is little loss due to throwing away the principal components that % correspond to dimensions with low variation. % -------------------- YOUR CODE HERE -------------------- xHat = zeros(size(x)); % You need to compute this xHat = u*[u(:,1:k)'*x;zeros(n-k,m)]; % Visualise the data, and compare it to the raw data % You should observe that the raw and processed data are of comparable quality. % For comparison, you may wish to generate a PCA reduced image which % retains only 90% of the variance. figure('name',['PCA processed images ',sprintf('(%d / %d dimensions)', k, size(x, 1)),'']); display_network(xHat(:,randsel)); figure('name','Raw images'); display_network(x(:,randsel)); %%================================================================ %% Step 4a: Implement PCA with whitening and regularisation % Implement PCA with whitening and regularisation to produce the matrix % xPCAWhite. epsilon = 0.1; xPCAWhite = zeros(size(x)); % -------------------- YOUR CODE HERE -------------------- xPCAWhite = diag(1./sqrt(diag(s)+epsilon))*u'*x; figure('name','PCA whitened images'); display_network(xPCAWhite(:,randsel)); %%================================================================ %% Step 4b: Check your implementation of PCA whitening % Check your implementation of PCA whitening with and without regularisation. % PCA whitening without regularisation results a covariance matrix % that is equal to the identity matrix. PCA whitening with regularisation % results in a covariance matrix with diagonal entries starting close to % 1 and gradually becoming smaller. We will verify these properties here. % Write code to compute the covariance matrix, covar. % % Without regularisation (set epsilon to 0 or close to 0), % when visualised as an image, you should see a red line across the % diagonal (one entries) against a blue background (zero entries). % With regularisation, you should see a red line that slowly turns % blue across the diagonal, corresponding to the one entries slowly % becoming smaller. % -------------------- YOUR CODE HERE -------------------- covar = (1./m)*xPCAWhite*xPCAWhite'; % Visualise the covariance matrix. You should see a red line across the % diagonal against a blue background. figure('name','Visualisation of covariance matrix'); imagesc(covar); %%================================================================ %% Step 5: Implement ZCA whitening % Now implement ZCA whitening to produce the matrix xZCAWhite. % Visualise the data and compare it to the raw data. You should observe % that whitening results in, among other things, enhanced edges. xZCAWhite = zeros(size(x)); % -------------------- YOUR CODE HERE -------------------- xZCAWhite = u*xPCAWhite; % Visualise the data, and compare it to the raw data. % You should observe that the whitened images have enhanced edges. figure('name','ZCA whitened images'); display_network(xZCAWhite(:,randsel)); figure('name','Raw images'); display_network(x(:,randsel));
参考资料:
Deep learning:十(PCA和whitening)
http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial