前言:
这节课来学习下Deep learning领域比较出名的一类算法——sparse autoencoder,即稀疏模式的自动编码。我们知道,deep learning也叫做unsupervised learning,所以这里的sparse autoencoder也应是无监督的。按照前面的博文:Deep learning:一(基础知识_1),Deep learning:七(基础知识_2)所讲,如果是有监督的学习的话,在神经网络中,我们只需要确定神经网络的结构就可以求出损失函数的表达式了(当然,该表达式需对网络的参数进行”惩罚”,以便使每个参数不要太大),同时也能够求出损失函数偏导函数的表达式,然后利用优化算法求出网络最优的参数。应该清楚的是,损失函数的表达式中,需要用到有标注值的样本。那么这里的sparse autoencoder为什么能够无监督学习呢?难道它的损失函数的表达式中不需要标注的样本值(即通常所说的y值)么?其实在稀疏编码中”标注值”也是需要的,只不过它的输出理论值是本身输入的特征值x,其实这里的标注值y=x。这样做的好处是,网络的隐含层能够很好的代替输入的特征,因为它能够比较准确的还原出那些输入特征值。Sparse autoencoder的一个网络结构图如下所示:

损失函数的求法:
无稀疏约束时网络的损失函数表达式如下:
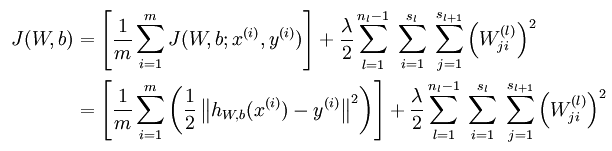
稀疏编码是对网络的隐含层的输出有了约束,即隐含层节点输出的平均值应尽量为0,这样的话,大部分的隐含层节点都处于非activite状态。因此,此时的sparse autoencoder损失函数表达式为:
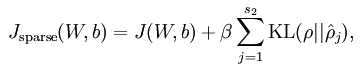
后面那项为KL距离,其表达式如下:
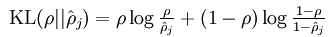
隐含层节点输出平均值求法如下:
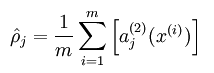
其中的参数一般取很小,比如说0.05,也就是小概率发生事件的概率。这说明要求隐含层的每一个节点的输出均值接近0.05(其实就是接近0,因为网络中activite函数为sigmoid函数),这样就达到稀疏的目的了。KL距离在这里表示的是两个向量之间的差异值。从约束函数表达式中可以看出,差异越大则”惩罚越大”,因此最终的隐含层节点的输出会接近0.05。
损失函数的偏导数的求法:
如果不加入稀疏规则,则正常情况下由损失函数求损失函数偏导数的过程如下:

而加入了稀疏性后,神经元节点的误差表达式由公式:

变成公式:
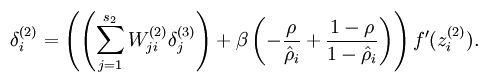
梯度下降法求解:
有了损失函数及其偏导数后就可以采用梯度下降法来求网络最优化的参数了,整个流程如下所示:
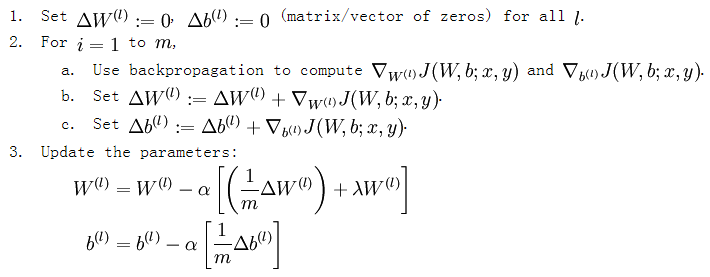
从上面的公式可以看出,损失函数的偏导其实是个累加过程,每来一个样本数据就累加一次。这是因为损失函数本身就是由每个训练样本的损失叠加而成的,而按照加法的求导法则,损失函数的偏导也应该是由各个训练样本所损失的偏导叠加而成。从这里可以看出,训练样本输入网络的顺序并不重要,因为每个训练样本所进行的操作是等价的,后面样本的输入所产生的结果并不依靠前一次输入结果(只是简单的累加而已,而这里的累加是顺序无关的)。
参考资料:
http://deeplearning.stanford.edu/wiki/index.php/Autoencoders_and_Sparsity