二叉搜索树即左孩子的值小于根节点,右孩子的值大于根节点。
二叉搜索树的插入:
即检查要插入的数(key,下文都用它表示)是否存在,若存在返回false,不存在即插入,在插入时,若key大于根节点,则插入到右子树中,更新根节点,依次类推;若key小于根节点,则插入到左子树中,更新根节点,以此类推。下面用图表示

现在要插入13,由二叉树的性质可知,13要插到10的右子树上,即

代码实现:
bool Insert(const k& key, const v& value)
{
if (_root == NULL)
{
_root = new Node(key, value);
}
Node* cur = _root;
Node* parent = cur;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
Node* node = new Node(key, value);
if (key > parent->_key)
{
parent->_right = node;
}
else
{
parent->_left = node;
}
return true;
}
二叉树的删除:
二叉树的删除要分三种情况,分别为:
a、删除的节点为叶子节点
b、删除的节点有一个子节点
c、删除的节点有两个子节点
第一种就不具体说了,直接删除即可。
下面分析第二种
如果删除的节点缺左子树就用右子树进行填补,同理,缺右子树就用左子树进行填补。下面用图说明

要删除1这个节点,即用1 的左子树填补1的位置,再将1删除。如下图

紧接着第三种情况,也是最复杂的一种。
要删除的节点有两个子节点,在这里定义删除的节点为del,firstInorder为以del为跟的树的最左节点,交换del和firstInorder的值,删除del即可,下面同样用图展示
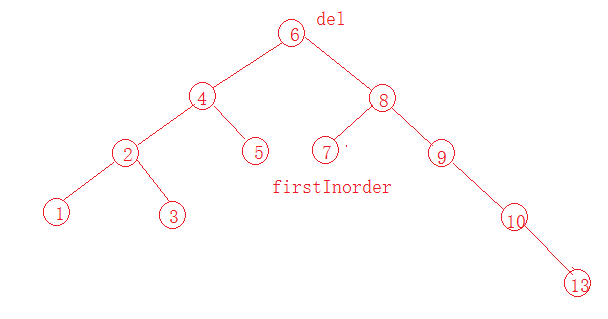
要删除6这个节点,首先找到最左节点7,因为7是右子树中最小的,交换6,7,删除6,此树仍然满足搜索树,如下图

代码实现如下
bool Remove(Node* root,const k& key)
{
//根节点为空
if (root == NULL)
{
return false;
}
//只有一个节点
if (root->_left == NULL && root->_right == NULL)
{
delete root;
root = NULL;
return true;
}
Node* parent = NULL;
Node* del = root;
while (del)
{
if (key > del->_key)
{
parent = del;
del = del->_right;
}
else if (key < del->_key)
{
parent = del;
del = del->_left;
}
else
{
break;
}
}
if (del)
{
if (del->_left == NULL)
{
if (del == root)
{
root = del->_right;
}
else
{
if (del == parent->_left)
{
parent->_left = del->_right;
}
else
{
parent->_right = del->_left;
}
}
}
else if (del->_right == NULL)
{
if (del = root)
{
root = del->_left;
}
else
{
if (del == parent->_left)
{
parent->_left = del->_left;
}
else
{
parent->_right = del->_right;
}
}
}
else
{
Node* parent = del;
Node* firstInorder = del->_right;
while (firstInorder->_left)
{
parent = firstInorder;
firstInorder = firstInorder->_left;
}
swap(del->_key, firstInorder->_key);
swap(del->_value, firstInorder->_value);
parent->_left = firstInorder->_right;
delete del;
del = NULL;
return true;
}
}
}
源代码如下:
template <class k,class v>
struct BSTNode
{
BSTNode<k, v> _left;
BSTNode<k, v> _right;
k _key;
v _value;
BSTNode(const k& key,const v& value)
:_left(NULL)
,_right(NNULL)
,_key(key)
,_value(value)
{}
};
template <class k,class v>
class BSTree
{
typedef BSTNode<k, v> Node;
protected:
Node* _root;
public:
BSTree()
:_root(NULL)
{}
public:
bool Insert(const k& key, const v& value)
{
if (_root == NULL)
{
_root = new Node(key, value);
}
Node* cur = _root;
Node* parent = cur;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
Node* node = new Node(key, value);
if (key > parent->_key)
{
parent->_right = node;
}
else
{
parent->_left = node;
}
return true;
}
bool Insert_R(Node*& _root, const k& key, const v& value)
{
if (_root == NULL)
{
_root = new Node(key, value);
return true;
}
if (key > _root->_key)
{
return Insert_R(_root->_right, key, value);
}
else if (key < _root->_key)
{
return Insert_R(_root->_left, key, value);
}
else
{
return false;
}
}
bool Find(const k& key, const v& value)
{
if (_root == NULL)
{
return false;
}
Node* cur = _root;
while (cur)
{
if (key == cur->_key)
{
return true;
}
else if (key < cur->_key)
{
cur = cur->_right;
}
else
{
cur = cur->_left;
}
}
return false;
}
bool Remove(Node* root,const k& key)
{
//根节点为空
if (root == NULL)
{
return false;
}
//只有一个节点
if (root->_left == NULL && root->_right == NULL)
{
delete root;
root = NULL;
return true;
}
Node* parent = NULL;
Node* del = root;
while (del)
{
if (key > del->_key)
{
parent = del;
del = del->_right;
}
else if (key < del->_key)
{
parent = del;
del = del->_left;
}
else
{
break;
}
}
if (del)
{
if (del->_left == NULL)
{
if (del == root)
{
root = del->_right;
}
else
{
if (del == parent->_left)
{
parent->_left = del->_right;
}
else
{
parent->_right = del->_left;
}
}
}
else if (del->_right == NULL)
{
if (del = root)
{
root = del->_left;
}
else
{
if (del == parent->_left)
{
parent->_left = del->_left;
}
else
{
parent->_right = del->_right;
}
}
}
else
{
Node* parent = del;
Node* firstInorder = del->_right;
while (firstInorder->_left)
{
parent = firstInorder;
firstInorder = firstInorder->_left;
}
swap(del->_key, firstInorder->_key);
swap(del->_value, firstInorder->_value);
parent->_left = firstInorder->_right;
delete del;
del = NULL;
return true;
}
}
}
bool Remove_R(Node*& _root, const k& key, const v& value)
{
if (root == NULL)
{
return false;
}
else if (root->_key < key)
{
return _Remove_R(root->_right, key);
}
else if (root->_key > key)
{
return _Remove_R(root->_left, key);
}
else
{
Node* del = root;
if (root->_left == NULL)
{
root = root->_right;
}
else if (root->_right == NULL)
{
root = root->_left;
}
else
{
Node* firstInorder = root->_right;
while (firstInorder->_left)
{
firstInorder = firstInorder->_left;
}
swap(del->_key, firstInorder->_key);
swap(del->_value, firstInorder->_value);
return _Remove_R(root->_right, key);
}
delete del;
}
}
void _Inorder()
{
Inorder(_root);
cout << endl;
}
public:
Inorder(Node* root)
{
if (root == NULL)
{
return;
}
Inorder(root->_left);
cout << root->_key << " ";
Inorder(root->_right);
}
};