poj 3469 Dual Core CPU【求最小割容量】

Dual Core CPU

Time Limit: 15000MS		Memory Limit: 131072K
Total Submissions: 21453		Accepted: 9297
Case Time Limit: 5000MS

Description

As more and more computers are equipped with dual core CPU, SetagLilb, the Chief Technology Officer of TinySoft Corporation, decided to update their famous product - SWODNIW.

The routine consists of N modules, and each of them should run in a certain core. The costs for all the routines to execute on two cores has been estimated. Let's define them as A_i and B_i. Meanwhile, M pairs of modules need to do some data-exchange. If they are running on the same core, then the cost of this action can be ignored. Otherwise, some extra cost are needed. You should arrange wisely to minimize the total cost.

Input

There are two integers in the first line of input data, N and M (1 ≤ N ≤ 20000, 1 ≤ M ≤ 200000) .
The next N lines, each contains two integer, A_i and B_i.
In the following M lines, each contains three integers: a, b, w. The meaning is that if module a and module b don't execute on the same core, you should pay extra w dollars for the data-exchange between them.

Output

Output only one integer, the minimum total cost.

Sample Input

3 1
1 10
2 10
10 3
2 3 1000

Sample Output

13

题意：由于越来越多的计算机配置了双核CPU，TinySoft公司的首席技术官员，SetagLilb，决定升级他们的产品－SWODNIW。SWODNIW包含了N个模块，每个模块必须运行在某一个CPU中。每个模块在每个CPU中运行的耗费已经被估算出来了，设为Ai和Bi。同时，M对模块之间需要共享数据，如果他们运行在同一个CPU中，共享数据的耗费可以忽略不计，否则，还需要额外的费用。你必须很好地安排这N个模块，使得总耗费最小。

割：源点s，汇点t在图V中把所有点分为两个集合S（源点在其中）和T=V-S（汇点在其中），如果把“起点在S中，终点在T中的”边全部删除，这样源点s就不能到达汇点t了，删去的这样的边的集合（S,T）叫做割

最小割：一个图中割有很多，其中所有边的权值之和最小的割叫做最小割

最小割的容量等于这个割上所有边的容量总和，          最小割的容量==最大流

题解：要求所有的模块在两个CPU中运行的费用最少，运用最大流知识，即求最小割的容量

建图：1、以两个cpu分别为源点和汇点，源点分别连接每个模块i，容量为Ai，模块i再连接汇点，容量为Bi
2、对于模块a和mokuaib在不同CPU中运行消耗的额外费用w，分别建立一条a->b的边容量为w和一条b->a的边容量为w；

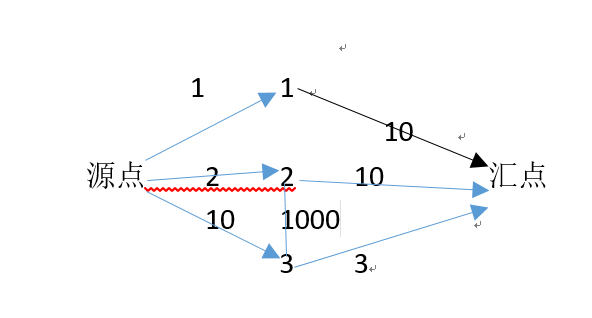
如图：因为一条路线有容量最少的那条边来限制流量所以的到的结果就是最小割

#include<stdio.h>
#include<string.h>
#include<queue>
#include<stack>
#include<algorithm>
#define MAX 100010
#define MAXM 1001000
#define INF 0x7fffff
using namespace std;
int n,m;
struct node
{
    int from,to,cap,flow,next;
}edge[MAXM];
int dis[MAX],vis[MAX];
int cur[MAX];
int ans,head[MAX];
void init()
{
	ans=0;
	memset(head,-1,sizeof(head));
} 
void add(int u,int v,int w)
{
	edge[ans]={u,v,w,0,head[u]};
	head[u]=ans++;
//	edge[ans]={v,u,0,0,head[v]};
//	head[v]=ans++;
}

void getmap()
{
	int i,j,a,b,c;
	for(i=1;i<=n;i++)
	{
		scanf("%d%d",&a,&b);
		add(0,i,a);
		add(i,0,0);
		add(i,n+1,b);
		add(n+1,i,0);
	}
	for(i=1;i<=m;i++)
	{
		scanf("%d%d%d",&a,&b,&c);
		add(a,b,c);
		add(b,a,c);
	}
}
int bfs(int beg,int end)
{
    queue<int>q;
    memset(vis,0,sizeof(vis));
    memset(dis,-1,sizeof(dis));
    while(!q.empty()) q.pop();
    vis[beg]=1;
    dis[beg]=0;
    q.push(beg);
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=head[u];i!=-1;i=edge[i].next)
        {
            node E=edge[i];
            if(!vis[E.to]&&E.cap>E.flow)
            {
                dis[E.to]=dis[u]+1;
                vis[E.to]=1;
                if(E.to==end) return 1;
                q.push(E.to);
            }
        }
    }
    return 0;
}
int dfs(int x,int a,int end)
{
    if(x==end||a==0)
    return a;
    int flow=0,f;
    for(int& i=cur[x];i!=-1;i=edge[i].next)
    {
        node& E=edge[i];
        if(dis[E.to]==dis[x]+1&&(f=dfs(E.to,min(a,E.cap-E.flow),end))>0)
        {
            E.flow+=f;
            edge[i^1].flow-=f;
            flow+=f;
            a-=f;
            if(a==0) break;
        }
    }
    return flow;
}
int maxflow(int beg,int end)
{
    int flow=0;
    while(bfs(beg,end))
    {
        memcpy(cur,head,sizeof(head));
        flow+=dfs(beg,INF,end);
    }
    return flow;
}
int main()
{
	while(scanf("%d%d",&n,&m)!=EOF)
	{
	    init();
		getmap();
		printf("%d
",maxflow(0,n+1)); 
	}
    return 0;
}