一、
问题:平均数——描述了数据的中心所在,但是,无法描述数据的分散情况。
目的:描述数据相对于,平均数的分布情况。
二、目录:
1.全距(极差)
2.四分位距
3.箱型图
4.方差、标准差
5.标准分
三、
1.全距(极差):
1.1 计算方法: 全距 = max(上界) - min(下界)
1.2
上界——数据集中的最大值max
下界——数据集中的最小值min
1.3 意义:描述了数据集的宽度。
1.4 优点:最简单
缺点:1.全距只描述了,数据的宽度,没有描述在上、下界之间的数据的真是形态是如何分布的。
2.全距极容易受到,异常值的影响。
解决方法:如何摆脱异常值影响——只使用数据中心周围的数值——四分位距
2.四分位距:
2.1 定义:
将数据一分为4,最小的四分位数称为下四分位数(Q1),最大的四分位数称为上四分位数(Q3),中间的四分位数即,中位数(Q2)。
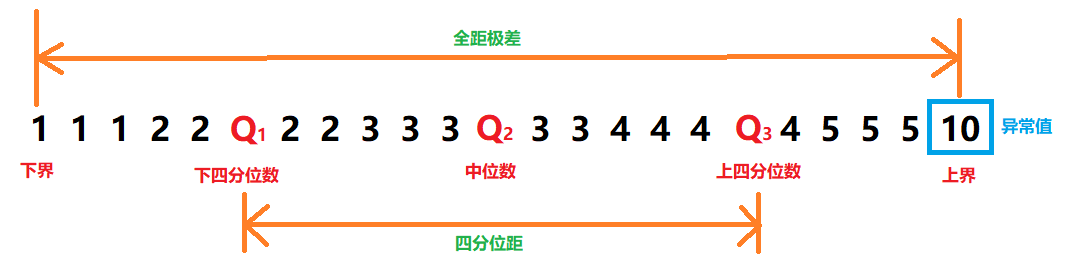
2.2 四分位距(IQR):
每两个四分位数之间的距被称为四分位距(IQR)
四分位距 = 上四分位数 — 下四分位数
IQR = Q3 — Q1
2.3 如何计算?
STEP1:排序
将所有的数据按照升序进行排列。———一共n个数据
STEP2:求下四分位数Q1的位置:
2.1 计算:n ÷ 4
2.2 a: 如果n ÷ 4结果为整数,则Q1位于n ÷ 4这个位置和下一个位置之间,取这两个位置上的数值的平均值。
b: 如果n ÷ 4结果不是整数,则将n ÷ 4结果向上取整,所得结果即为的Q1位置
eg: n = 6时,n ÷ 4 = 1.5,向上取整——>得2,Q1位置为2
STEP3:求下四分位数Q3的位置:
2.1 计算:3n ÷ 4
2.2 a: 如果3n ÷ 4结果为整数,则Q3位于3n ÷ 4这个位置和下一个位置之间,取这两个位置上的数值的平均值。
b: 如果3n ÷ 4结果不是整数,则将3n ÷ 4结果向上取整,所得结果即为的Q3位置
eg: n = 6时,3n ÷ 4 = 4.5,向上取整——>得5,Q3位置为5
STEP4:求IQR:
IQR = Q3 — Q1
2.4 优点:与全距相比,四分位距,可以较少的受到异常值的影响。
原因:四分位距仅仅使用了位于中间部分的50%的数据,而异常值是不可能位于中间部分的,从而将数据中的异常值剔除了。
缺点:a.只度量了数据的分散性,但是没有度量数据的稳定性。
b.由于为了剔除极端值异常值,只考虑了部分数据,不能完全反映数据整体。
2.5 意义:可以对不同的数据集进行比较,而且比较结果不会被异常值扭曲
(全距极差存在问题:全距非常容易收到异常值的影响,只要掺进去一个异常值,求出的全距就会是天差地别
采用四分位距,只关注数据中央的50%数据,这样就排除了异常值的影响。)
3. 百分位数:
3.1 将数据分成100份,起作用的数值被称为百分位数。
3.2 第K百分位数,位于数据的k%出的数值,记为:Pk
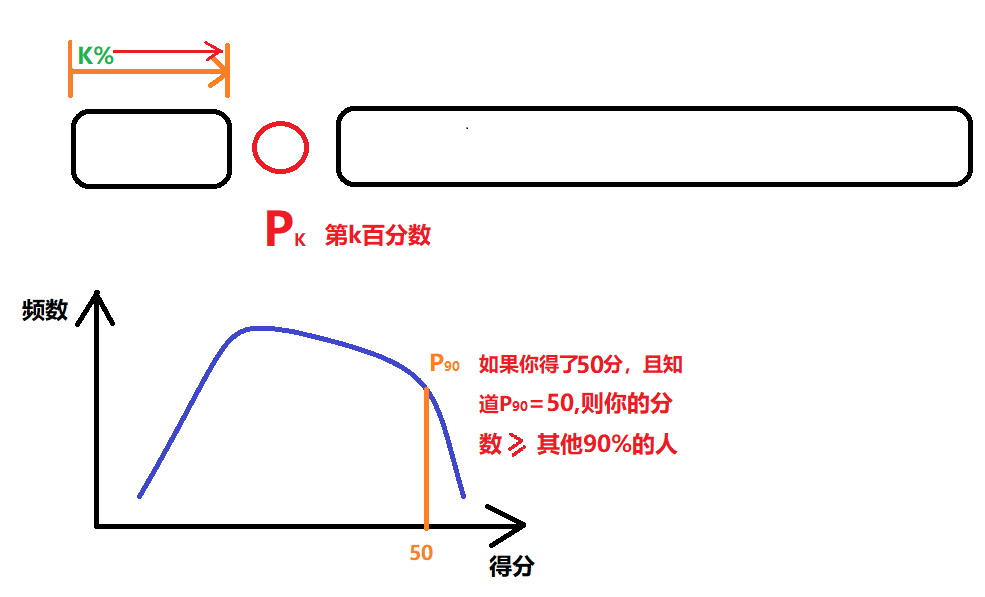
3.3 用途:a. 通过百分位数确定某个数值相对于其他数值的高低。
b.划分名次、档次、排行。
3.4 Pk 的求法:
STEP1:将所有数值按照升序排序。
STEP2:计算k × (n ÷ 100)
STEP3: a.如果k × (n ÷ 100) 的值为整数,则第k百分位数处于k × (n ÷ 100)位和下一位数之间,去这两个数的平均值,即为Pk
b.如果k × (n ÷ 100) 的值不是整数,将结果向上取整,得到的结果即为第k百分位数的位置。
4.箱线图
4.1 作用:用来显示各种距。
4.2 画法:2种
法一:
STEP1:先画出一个箱子,箱子的左边是下四分位数Q1,右边是上四分位数Q3。
STEP2:在箱子中,画一条直线,标注出中位数Q2
STEP3:在箱子两边,画出“线”,显示出数据的上界max、下界min和全距
法二:
5.方差σ2与标准差σ:
5.0 为什么有了全距和四分位距,还要有方差、标准差?
方差σ2与标准差σ的出现是由于,四分位距IQR存在一些问题。
a.四分位距IQR只度量了数据的分散性,但是IQR没有度量数据的稳定性。
b.由于为了剔除极端值异常值,IQR只考虑了部分数据,不能完全反映数据整体。
5.1 如何计算?
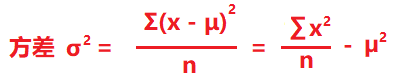
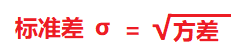
标准差的计量单位与相应的数据的单位相同
5.2 意义?
标准差σ——度量了数据与均值的距离,从而描述了数据的分散性——各个数值相对于均值而言,如何变化。
如果标准差较大,则意味着数值往往距离均值较远;如果标准差较小,则数值往往距离均值较近。
6.如何对均值不同,标准差也不同的,不同的数据集进行比较?————标准分Z
6.1 如何计算标准分Z?
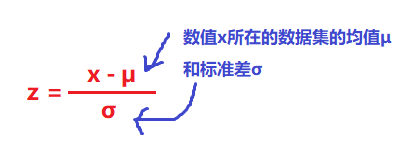
6.2 标准分有何意义?
标准分将不同的数据分布,都转化为成一个均值μ=0,标准差σ=1的标准分布。
标准分z,表示的是相对于均值0的位置。
现在的问题:
1.了解不同的箱线图形式
2.标准分的意义。