hello,最近yogurt给大家的更新很频繁哦~~今天要分享的内容是紧接着前面两篇的内容做的扩展~~
我们不仅要求取某地区在地球椭球体这个三维空间中的面积,还要与该地区投影到二维空间后平面多边形的面积进行对比。怎么求取二维平面多边形的面积,大家可以看看我之前写过的《求解多边形面积2S= Σ【Xi (Yi+1-Yi-1)】,(i属于1~n),公式解析及编程实现》http://www.cnblogs.com/to-sunshine/p/7642222.html。至于怎么进行兰伯特投影墨卡托投影,大家可以参考我之前写过的《.gen地图文件的投影编程实现(以墨卡托投影和兰伯特投影为例)》http://www.cnblogs.com/to-sunshine/p/6048438.html。
============================yogurt小课堂开课了===========================
下面yogurt要跟大家分享这次需要用到的知识点:
地球椭球体表面上的梯形面积:
取长度很小很小的一个长和一个宽,组成的梯形是非常小的,近似可以看作矩形。那么 S = 长 X 宽 ,如下图:
 (图来自我老师的PPT)
(图来自我老师的PPT)
我们知道 AB = CD ,是南北方向上的边长,假设与任意一条经线平行。由上节的知识,我们不难知道: AB = CD = M X dφ (dφ是AD所在纬线与BC所在纬线的纬度间隔,很小);
同样,由于纬度间隔非常小,可以近似看作 BC ≈ AD ,是东西方向上的边长,假设与任意一条纬线平行。由上节的知识,我们也不难知道: BC ≈ AD = r X dλ (dλ是AB所在经线与CD所在经线的经度间隔,很小),而 r = N X cosφ(φ看作AD所在纬线或者BC所在纬线的纬度,由于间隔很小,所以只要所有梯形统一用上边的或者统一都用下边的纬度即可)。因此,BC = AD = N X cosφ X dλ 。
综上,便能够得到地球椭球体上梯形的面积 dS = (M X dφ) X (N X cosφ X dλ)= M N cosφ dλ dφ ,那么 S = ![]() 。
。
对于每一个小梯形,用前后两个点的平均纬度作为 φ2,以该区域的最低纬度作为 φ1,dφ = φ2 - φ1 ;前后两个点的经度对应 λ1、λ2,再利用积分的原理就可以计算得到椭球体上的某区域的面积啦!
=================================下课了================================
假设我们拿到的数据是某区域墨卡托投影后的二维平面上一系列的区域边界点数据,那么我接下来的步骤将分为六步:1、计算二维平面上的墨卡托投影后的平面面积 S1 --> 2、墨卡托投影反算,得到每个点在地球椭球体上对应的经纬度坐标 --> 3、计算地球椭球体上该区域的面积 S2 --> 4、把该区域进行兰伯特投影得到二维平面上又一系列的区域边界点数据 --> 5、计算二维平面上的兰伯特投影后的平面面积 S3 --> 6、对比三种面积的区别。
1、计算二维平面上的墨卡托投影后的平面面积 S1
程序如下:

2、墨卡托投影反算,得到每个点在地球椭球体上对应的经纬度坐标
先利用墨卡托投影反解公式,计算B、L,其中对于求解 L 需要用到 K ,K 的值由公式求出;对于求解 B,则需要设定一个初始值,然后进行迭代求解,直到前后两次计算出的 B 之差小于0.00000000001,则认为后一次计算的 B 的值为最终解。
程序如下:


在ArcGIS中查看墨卡托反算前后的数据,对比显示如下:

反算前 反算后
3、计算地球椭球体上该区域的面积 S2
因为ds足够小,所以把梯形近似看做一个矩形来计算,矩形的长为东西方向的弧长,宽为南北方向的弧长。根据弧长计算公式:弧长=半径*弧度,涉及到子午圈曲率半径M和主法截面曲率半径N的计算公式。通过查阅资料,可知:
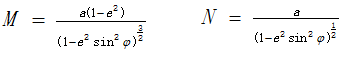
南北方向上的弧长d=M*d;东西方向上的弧长d=N*d
对于每一个小梯形,用前后两个点的平均纬度作为 φ2,以该区域的最低纬度作为 φ1,前后两个点的经度对应 λ1、λ2,再利用积分的原理来计算得到椭球体上的该区域面积。
程序如下:
先声明和赋值程序中将会用到的基本数据长半轴a、第一偏心率e、基准纬度(江苏省最低纬度)B;并通过指向矢量文件的指针获得前后两点的纬度B1、B2和经度L1、L2。用TB来代替2-1,用AB来代替(1+2)/2:

计算小梯形的面积积分公式所需要用到的参数K、A、B、C、D,带入公式进行计算面积:

4、把该区域进行兰伯特投影得到二维平面上又一系列的区域边界点数据
这里参考《.gen地图文件的投影编程实现(以墨卡托投影和兰伯特投影为例)》http://www.cnblogs.com/to-sunshine/p/6048438.html。
5、计算二维平面上的兰伯特投影后的平面面积 S3
方法同第一步,只是带入的数据不同。
6、对比三种面积的区别
整个程序主函数如下:

运行后结果如下:

可见,进行Albers等积投影之后,矢量面的面积变化误差相比之整体面积来说较小,所以视为等积投影是成功的。