Lecture 14：Radial Basis Function Network

Lecture 14：Radial Basis Function Network

14.1 RBF Network Hypothesis

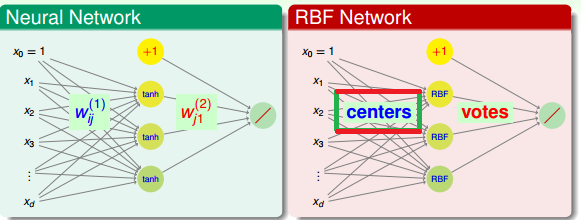
                                 图  14-1 RBF network

      从图 14 -1 中可以看出，RBF NNet 没啥特色。就是用 RBF 核作为激活函数。为什么还要 RBF NNet 呢？难道是大家公认 RBF 核很好？数学公式多了去，岂不是有无穷多个 NNet 呢。

需要参考 《RBF神经网络和BP神经网络有什么区别？》 。

       首先 RBF NNet 计算速度很快。因为 RBF NNet 真的只有 3 层，图 14-1 的右半图是真的啊不是表意的啊（图 14-1 的左半图是表意的啊，不一定是 3 层啊啊）。

其次， 在生物学中有这样的结论："大脑里的神经元就是这么工作的。你闻到花香的时候，不会刺激到感受辣味的神经元"。RBF 算是局部激活函数，离记忆点越近越容易被激活。

                                              图  14-2

14.2 RBF Network Learning

     本小节的内容，基本上是在讨论为什么不用 Full RBF NNet以及 Full RBF NNet 的特性。后面很自然地引出第 3 小节的内容

14.3 k-Means Algorithm

 

                                                    图  14-3

       将相近的样本点聚类后用一个代表去表面这个 cluster 的特性，通过这种方法化简 Full RBF NNet。现在的问题就是如何 cluster， 以及如何找出 代表。

我们采用 alternative minized 方法，如图 14-4 所示。计算出 cluster 和 u 后代入 RBF NNet 网络。

                                       图  14-4 

14.4 k-Means and RBF Network in Action

      k-Means 的例子！

题外话：

 T1： CNN 、RBF NNet 这些 NNet 都包含着生物学意义，其它的 NNet 也应该包含着一定的意义！