Lecture 13. Hazard of Overfitting
13.1 What is Overfitting
Overfitting 是什么? 简而言之就是模型训练集上表现要好于在测试集上表现!在第 12 节关于 feature transform 讨论时,我们知道可以用复杂的算法获取到很小的 Ein, 但是这不能代表 Eout 很小!
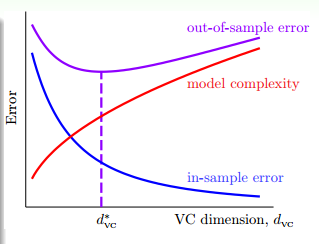
图 13-1
过拟合的原因有哪些?我们以开车为例,出车祸的原因不外乎是车开太快、路况不好、对路面的观察不够。对应到机器学习中过拟合就是模型太复杂、数据有噪声、数据量不够。
简言之就是,工具(模型复杂)、操作对象(数据噪声)、操作者(数据过少,观察数据有问题)三者有问题。
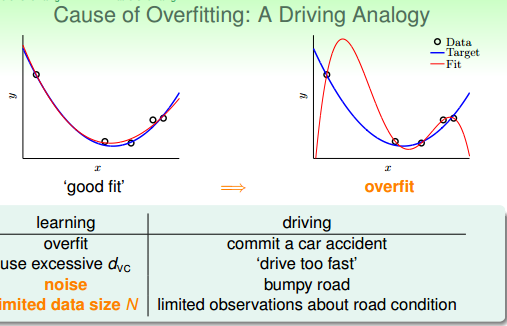
图 13-2 用车祸来类比过拟合
13.2 The Role of Noise and Data Size
样例一:我们用 10 次和50 次多项式产生测试数据, 10-th 多项式的产生数据加上噪声。最终生成的测试数据如图 13-3 所示,10-th 多项式生成的数据加上了噪声,所以不能完全拟合。50-th 多项式生成的数据没有噪声所以能完全拟合。
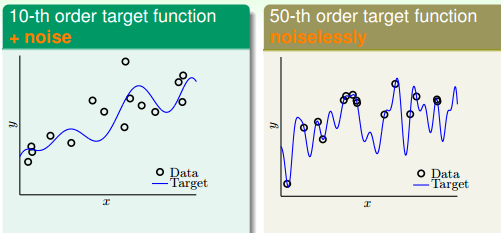
图 13-3 测试数据
现在我们在 H2 和 H10 选择演算法,得出的结果如下表所示
| 10-th data | g10 | g10 |
| Ein | 0.050 | 0.034 |
| Eout | 0.127 | 9.00 |
| 50-th data | g2 | g10 |
| Ein | 0.029 | 0.00001 |
| Eout | 0.120 | 7680 |
从表中可以看出二次多多项式的 in-sample 误差都要大于 10 次多项式的误差(如果 10-th data 没有加上噪声的话, 10-th 多项式的数据要比二次多项式要好!!!。 同理 50-th 多项去拟合 50-th 多项式产生的数据会很好,但是我们使用二次、十次多项式去拟合的,所以不论是二次还是十次多项式都会有 in-sample 误差,且 10-th 多项式的 in-sample 误差肯定会略小。但是令人不解的是 10 次多项式的 out-sample 误差居然要大于 2 次多项式的 out-sample 误差!),直观上很难理解 2 次和 10 次多项式的 out-sample误差。这是为什么呢?这个问题要用之前学过 Ein、Eout 和噪声的关系说起,如图 13-3 所示。
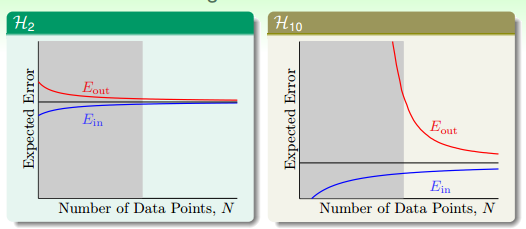
图 13-4 Learing Curves
对于 10-th 多项是生成的有 nosie 的数据。10-th 多项式的学习能力强所以 in-sample 误差小,但是在 inputs 较少的情况 2-th 多项式的 out-sample loss 可能要比 10-th多项式的要低 (之前的误解,认为 10-th 多项式的泛化能力肯定要比 2-th 多项式的要差,即 10-th 的多项式的过拟合过的无可救药)。
对于 50-th 多项式生成的数据,本身就不能用 2-th、10-th 的多项式去拟合(后续章节将这个称之为 Deterministic Noise)
13.3 Deterministic Noise
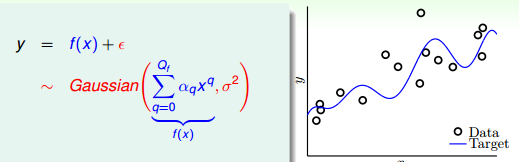
图 13-5 生成数据图
现在来生成测试数据,测试数据上加上服从高斯分布的噪声(即噪声服从正太分布,为随机噪声)。h2 和 h10 演算法的过拟合效果图如图 13-6 所示。 用颜色代表过拟合程度,x 轴为训练数据集数量,y 轴则是噪声强度和目标复杂度。
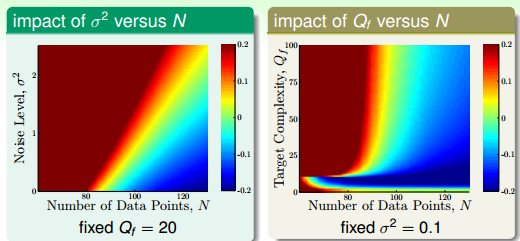
图 13-6 Overfitting 结果图 (Qf 目标复杂度,σ 噪声水平)
这样,我们就发现有四处会发生过拟合的点, 如图13-7 所示。图 13-6 能解释前三种原因,第四种原因 excessive power 是用太复杂的模型去学习太简单的数据,肯定会发生过拟合

图 13-7 Reason for Overfitting
Deterministic Noise 比较难理解,简单的解释就是用弱学习器去学习强数据(汗),就像是小孩拉大车肯定会出事。
13.4 Dealing with Overfitting
既然我们已经知道过拟合的原因,我们该如何避免过拟合呢?林老师给出了自己的建议以及个人经验分享--- 如何获取更多的资料 data Cleaning/ Pruning(又见到我们的老朋友的)

图 13-7
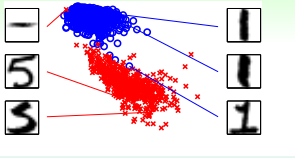
图 13-8 data cleaning
题外话:
1. 目前没见过 data cleaning 和 data pruning 的例子啊!
2. 除了噪声以外,特征数据还有多重共线性(目前只知道多重共线性这个名词,不知道它对决策树、lr、梯度下降的影响)等问题。很多机器学习算法理论都是在建立在 feature iid 分布上,但是采集的来的 feature 不可能完全是 iid 分布。这就需要后续的矫正。
不知道决策树的剪枝是不是能起到抑制多重共线性的影响? 剪枝能起到抑制因 feature dirty 所带来的不利影响?
3. any supervised feature selection (using correlation with class labels) performed outside of the model performance estimation using cross validation (or other model estimating method such as bootstrapping) may result in overfitting
T1: 图示过拟合

图 T1-1