Lecture 12: Nonlinear Transformation
12.1 Quadratic Hypothesis
现在我们碰到一个新的问题,如何来给如图 12-1 所示的线性不可分数据做分类? 我们之前只学过 linear classification 和 linear regression 。没有学过 nonlinear 算法。
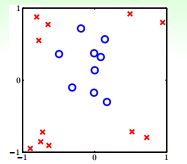
图 12-1 线性不可分数据集
图 12-1 所示的数据可以用用圆(椭圆也可以)分开, 如图 12-2 所示
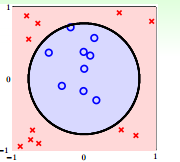
图 12-2
$$h_{SEP}(x) = sign(-x_{1}^2 - x_{2}^2 + 0.6 ) $$
公式 12-1 等于是将线性不可分的数据集映射成一个线性可分的数据集,如图 12-3 所示

图 12-3
将 feature 映射到 z space, 可以解决 "任何" 形状分类问题。 还是有个问题,我怎么知道有 xn 的阶数?如果不知道 xn 的阶数,后续的计算又该怎么算呢?目前我们只知道在 x space 的数据,但是到 z space 数据以及 z space 的相关参数
12.2 Nonlinear Transform
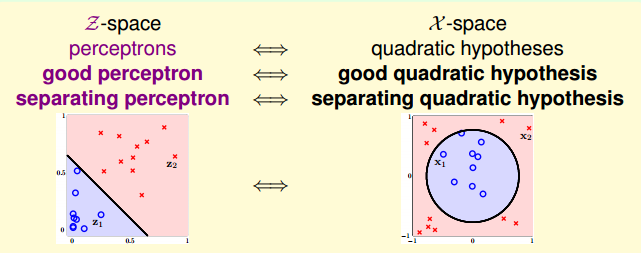
图 12-4
线性转换步骤如图 12-5 所示, 但是问题的是如何求出映射函数?
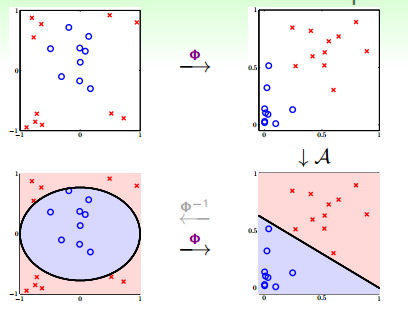
图 12-5
自从有了 feature transformation, 就等于打开 pandora box。 所有算法都可以和 feature transformation 组合!!!
在第三讲就使用 feature transformation ,不过当时没有意识它的意义。
12.3 Price of Nonlinear Transform
使用 feature transformation 能把 Ein 降的很低,这固然很好。但是 feature transformation 不是没有问题

图 12-6 大的计算和储存代价

图 12-7 很大的自由度
计算和存储代价变大,自由度变大(回忆之前章节中关于自由度的讨论)。自由度变大就意味可调参数过多,容易过拟合就像图 12-8 所示

图 12-8 泛化误差
现在有个问题,我们怎么知道该不该使用 feature transformation ? 对图 12-2 所示的数据集,我们似乎可以用眼睛去判断该不该用 feature transfromatin。但是对于更高维的,就没有好的办法。
事实上,我们不能用眼睛去做判断? 因为你用 brain 处理有限的采样数据。这个不能推广到更多的采样数据,这样会踩雷的(没认真听,感觉是应该是这样的)
12.4 Structured Hypothesis Sets
本节来讨论一个 hypothesis set 的有趣性质,看图说话 (只对 map 到 z-space 的有效)
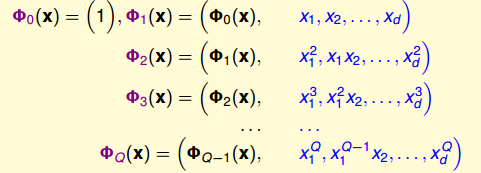
图 12-9
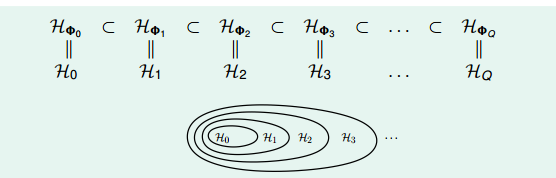
图 12-10
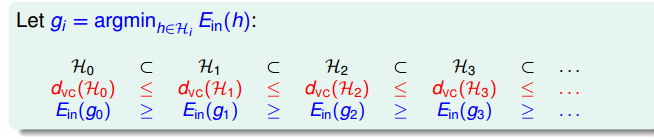
图 12-11
最后,放上老朋友图 12-12
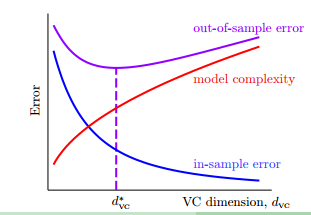
图 12-12
将本节理论应用于神经网络会怎么样?
题外话:
1. 如何计算 Nonlinear 的 VC Dimension ?
2. 潜意识中总认为 Nonlinear 的泛化误差要比 Linear 的要大,这个该怎么克服呢?
3. 你觉得本节 nonlinear transform 给你最大的启示是什么?
算法有一套数学公式做证明的, 应该是可以将数学公式 linear 部分用 nonlinear 来替换(这只是一种启示,不是真的可以简单、机械地做替换就可以的)。初学算法时,会用简单的线性算法来入门。这是因为线性算法简单,比较好解释(比如可以画图解释,有的还有几何意义解释如 linear regression)。我觉得不该将线性和非线性这两个概念对立起来, 而是不看具体的数学表达式而是关注更加内涵的东西。 不要太关注这些表像,要关注数学上的东西。没法说清楚~~~,希望我自己别忘了那种感觉
4. x space to z space 称之为 feature tranformation, 后续 《技法》课程就是围绕着 feature transformation 展开的。 为什么要 map x-space to z-space ?
5. VC Dimesion 相关章节还算是偏理论,现在这些内容给我的感觉还是偏技法? 是要用这些章节来引出某些重要的概念? 还是有其它的原因?
6. 在第十四节第二小节有个有关本节的小问题
7. 用 feature transformation 可以得到非线性的分类边界,有的算法如决策树天然就有非线性分类边界
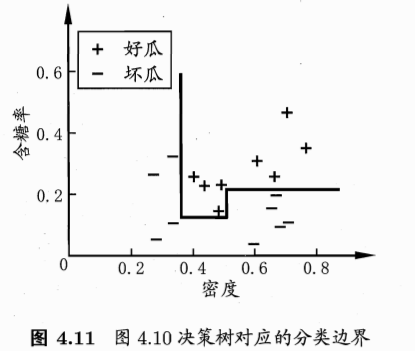
图 12-13
8. 欣赏一下 Adaptive Boosting 分类边界
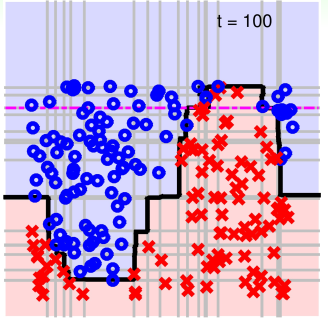
图 12-14
9. 欣赏一下 random feature selection 下的 C&RT 树的边界
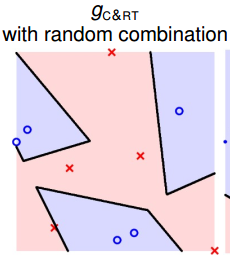
图 12-15