Lecture 11: Linear Models for Classification
11.1 Linear Models for Binary Classification
回顾一下,我们学习过的线性分类算法都有一个 linear scoring fuction: s = wTx (让我想到几个关键词,权重、特征转换)
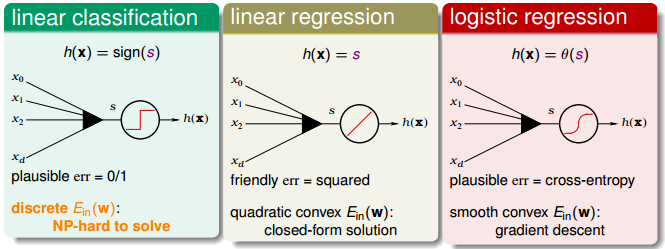
图 11-1
从图 11-1 中可以看出三种算法, linear classification、linear regression、logistic regression 各自不同的特性。 linear classification 是个 NP hard 问题, linear regression 和 logistic regression 都能有不错的解法。现在我们想一下能否通过 linear regression,logistic regression 或其它已经学习过算法来做 lineare classification 问题(记得在之前的章节中有过用 linear regression 来做linerar classifcation 的 讨论,最终在本节会用 ln2 交叉熵损失函数来做 linear classification 的损失函数的上界,因为 ln2 交叉熵损失函数要比 linear regression 损失函数更接近 0/1 损失函数)。
接着上一段的讨论,现在的问题是 linear regression、logistic regression 的损失函数和 linear classification 的关系(几何关系,谁包裹了谁,谁是谁的上界等等)。对于 binary classification 问题, y ∈{-1, +1} (当然你可以设定 y ∈{0, 1} 等其它集合,当然算法函数也要跟着换)。为了后续的讨论方便,我们来做些数学公式转化。对 linear classification . h(x) = sign(x) ---> err(h, x, y) = [sign(h(x)) != y] = [sign(y*h(x)) != 1]。对 linear regression、logisitic regression 如法炮制可以得出如图 11-2 所示的损失函数。

图 11-2 三种算法的损失函数
我们将图 11-2 所示的损失函数画成图,即图 11-3。ce 是交叉熵损失函数,在本图中是 logistic regression 的损失函数。 sqr 是 linear regression 损失函数。
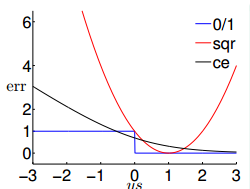
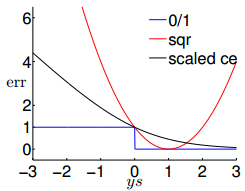
图 11-3 图 11-4
从图 11-3 中可以看出, sqr 曲线可以用于replace 0/1 损失函数,但是误差太大了。 ce 曲线在大部分区间都可以用于 replace 0/1 损失函数,但是在小部分区间不行。我们对 ce 损失函数进行放缩,即用 ln2 replace lne ,最终得到的结果如图 11-4 所示。最后给出用 0/1 损失函数的一个上界,如图 11-5 所示。

图 11-5
现在来总结本小节内容,如同图 11-6 所示

图 11-6
最后林老师给出自己的建议,如图 11-7 所示。 1. linear regression 可以用于计算出 PLA/pocket/logistic regression 所需的 w0.(以后还能看到用随机森林来选特征, 用 svm 来计算 b 和 w 用于 kernel logistic regerssion 等等) 2. logistic regression 和 pocket 的计算量差不多,这样的话就更应该使用 logistic regression to replace pocket(我还不知道 pocket 是个啥)!

图 11-7
11.2 Stochastic Gradient Descent
我们来回顾一下之前学过的两种迭代方法, PLA 所用的迭代方法即每次选一个点来更新向量 w 和 logistic regression 所用的 GD。
PLA 选用的算法每次只要用一个点, logistic regression 则要用所有的point 来更新 w 。这样的话, logistic regression 的计算量就很大!
我们在计算 logistic regression 能不能也像 PLA 一样,每次只用一个点来更新 w 呢(如果你要求的是精确解,那我告诉你这应该是不合理的。如果只要符合一定精度的解,应该是可以的)。
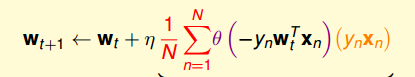
图 11-8 logistic regression GD 损失函数
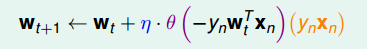
图 11-9 logistic regression SGD 损失函数
使用 SGD 还有一个问题有待解决,即如何知道什么时候停止迭代。林老师给出的建议的是 t 很大。林老师还建议将 η 设为 0.1 (0.1126)
Q1: 实际应用的 logistic regression 是 sgd 还是 mbd 呢?
林老师讨论问题的思路还是很清晰,不像其他的课程突然冒出来一个数学名词搞得人不知所云。
11.3 Multiclass via Logistic Regression
在西瓜书第三章节中有关于 OVR, OVO 的讨论。 不论是 OVR 或 OVO 的计算量都很大,如果神经网络做多分类也是用 OVR 或 OVO 做多分类,那计算量也太大了。
11.4 Multiclass via Binary Classification
还是有关 OVR 和 OVO 的讨论, 不赘述
题外话:
T1:regression并不一定会用square loss。square loss的优点是便于理解和实现,缺点在于对于异常值它的鲁棒性较差(来自知乎 https://www.zhihu.com/question/54626685 )。在《技法》的第 6 节中提到了 Tube Regression。我还记的另外一个词——勒让德多项式。