傅里叶变换 fft_generic halcon

傅立叶变换(FT, Fourier Transform)的作用是将一个信号由时域变换到频域。其实就是把数据由横坐标时间、纵坐标采样值的波形图格式，转换为横坐标频率、纵坐标振幅(或相位)的频谱格式。变换后可以很明显地看出一些原先不易察觉的特征。
离散傅立叶变换(DFT)的算法属于线性变换。由于对每个采样点，都要做一次全部点的加权求和的运算，因此当采样点比较多时，运算速度会很慢。
快速傅立叶变换(FFT)是DFT的快速算法，运算结果和DFT是相等的。其原理是利用权值的对称性与周期性，把采样点分解成两份，每份的点数是原来的一半，这样运算量也会减半。然后可以继续分解为4份、8份、16份……以此不断提升效率。

波形的公式：

采样植(y) - 纵坐标轴代表采样点的值
时间(t) - 横坐标轴代表时间，或者代表当前是第几个采样点
振幅(A) - 也叫幅度，代表波的高度(峰值)
圆频率(ω) - ω=2π*f，f代表频率
相位(ω*t) - 是个角度，一般用弧度制表示，弧度制的0～2π，代表0度到360度



采样点数量(N) - 采样的数据是离散的，常常用散点来表示，下图共有20个采样点。

频率(f) - 是单位时间内完成振动的次数，f=波的重复次数/N。



假如一个波的图形为：采样点数量(N)=200，振幅(A)=3，频率为10个波，即3*sin(2π*10/200)。

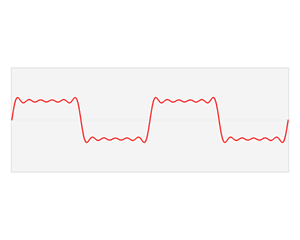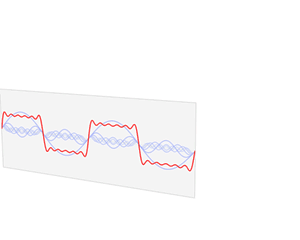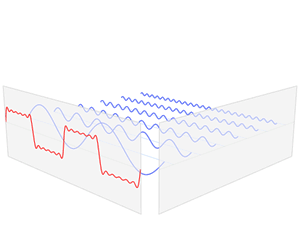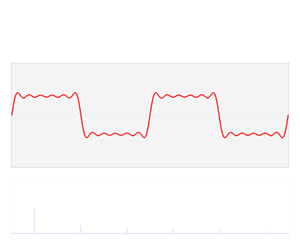
经过傅立叶变换后，可以看到在大约10的位置有一条竖线，由此很容易看出，频率为10个波。由于变换的结果是个对称图形，因此在右边200-10的对应位置也会出现一条竖线。变换后的数据，除了这两条竖线以外，其它值的都近似为0，是个稀疏矩阵。


运算结果是复数，输出值取复数的模(绝对值)。复数的模 = 实部的平方+虚部的平方,再开平方 = sqrt(real^2+imagine^2)


如果只为提取特征的话，使用上面的输出值就可以了。如果想得到标准的振幅和频率值，那么：
振幅 = 输出值/(N/2) = 300/(200/2) = 3
频率 = 波的重复次数/N = 10/200 = 0.05

Matlab:


N = 200; % 采样点数量
A = 3; % 振幅
fv = 10; % 波的重复次数
f = fv / 200; % 频率
t = [1:200]; % 时间


y = A * sin(t*2*pi*f); % 生成波形采样数据
plot(y); % 显示时域图


figure;
Y = fft(y, N); % FFT变换
plot(abs(Y)); % 显示频域图


--------------------------------------------
傅立叶变换入门：http://news.cnblogs.com/n/209014/
FFT是基于复数运算的，而实际采样点的数据一般是实数，因此要转换成复数形式。标准的做法是复数的实数部分为采样点的实数数据，虚数部分全部填0。(但这样做会有一定运算效率的问题，因为填0的部分也参与运算，对此也有一些优化算法。)