1.思维导图及学习体会
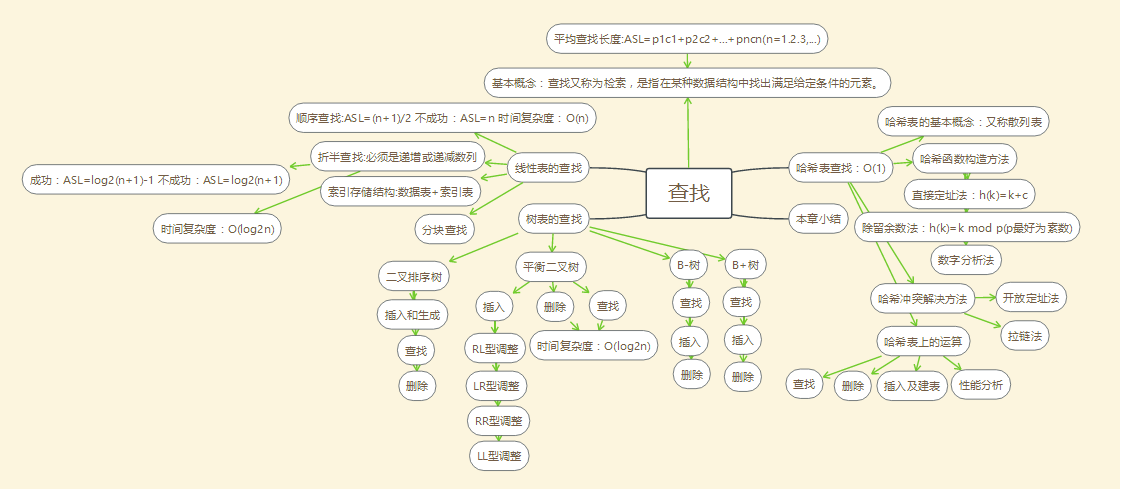
1.1 思维导图
1.2 学习体会
本章主要学习了多种的数据查找方法,以及各种查找方法的评价指标。
通过学习,知道了查找分为两种,一种是静态查找,一种是动态查找。静态查找,就是仅仅作查询和检索的功能,而动态查找则是在静态查找的基础上增添了增加数据和删除数据的功能。通过查找算法的评价指标(ASL),我们能比较各算法的优劣。ASL是指找到(找不到)查找表中记录平均需要的关键字比较次数
虽然查找对代码要求不高,但是涉及的内容更广更全面了同时也暴露了前面知识的缺漏,而且查找这章除了要求的代码外更多的是关于平衡树的调整操作,B树的删除增加调整操作等,还有关于各种查找方式对应的查找效率ASL的计算是不同的,要搞清楚这些计算首先得先清楚这些查找的原理然后再记忆其ASL的计算方式才不容易混淆。
哈希表的查找就相对要简单些。有了以前的一些的积累,哈希表的使用要相对轻松些。在原有的基础上补充了哈希冲突的相关问题,学习了解决哈希冲突的一些方法,如线性探测法、拉链法。
2.PTA实验作业
2.1 题目1:6-3 二叉搜索树中的最近公共祖先 (25 分)
2.1.1 设计思路
···
int find(Tree T, int x)
{
if T为空 then return 0
end if
if x 等于关键字 then
return 1
else if x 大于 关键字
调用函数find(T->Right, x)
else
调用函数find(T->Left, x)
end if
}
int LCA(Tree T, int u, int v)
{
if T 为空 then 返回ERROR
end if
if find(T, u) 返回0或者find(T, v)返回0 then 返回ERROR
end if
if T->Key 大于等于u并且T->Key小于v或者 T->Key 小于等于 u并且T->Key 大于等于 v then
返回 T->Key
if u > T->Key then
LCA(T->Right, u, v)
else if u < T->Key then
LCA(T->Left, u, v)
}
···
2.1.2 代码截图

2.1.3 PTA提交列表说明。

这道题老师上课的时候讲过,所以做起来挺简单的,然后很顺利在编译器上调了几次就AC了
2.2 题目2:6-2 二叉搜索树的操作集
2.2.1 设计思路
Position FindMin(BinTree BST)
if BST 不为空 then
if BST的左孩子不空 then
递归调用函数 FindMin(BST->Left);
else
返回BST;
end if
Position FindMax(BinTree BST)
if BST 不为空 then
if BST右孩子不为空 then
while BST右孩子不为空
BST = BST->Right;
end while
end if
end if
返回 BST;
BinTree Insert(BinTree BST, ElementType X)
if BST为空 then
定义BinTre类型结点p;
申请动态空间;
X存入p的数据域;
p的左右孩子初始化为空;
BST = p;
else if X < BST->Data then
BST->Left = Insert(BST->Left, X);
else if X < BST->Data then
BST->Right = Insert(BST->Right, X); //利用递归来进行数据的插入
end if
返回 BST;
BinTree Delete(BinTree BST, ElementType X)
if BST 为空 then
输出Not Found
else
if X < BST->Data then
BST->Left = Delete(BST->Left, X);
else if X > BST->Data then
BST->Right = Delete(BST->Right, X);
else if X = BST->Data
if BST的左右孩子都不为空 then
新建BinTree类型结点p;
p = FindMin(BST->Right);
BST->Data = p->Data;
BST->Right = Delete(BST->Right, BST->Data);
else
if BST的左孩子为空 then
BST = BST->Right;
else if BST右孩子为空 then
BST = BST->Left;
end if
end if
end if
返回 BST
Position Find(BinTree BST, ElementType X)
if BST为空 then
返回空值;
if BST->Data == X then
返回BST结点;
else if X < BST->Data then
利用递归找下一个左孩子结点;
else if (X > BST->Data)
利用递归找下一个左孩子结点;
返回BST
2.2.2 代码截图

2.2.3 PTA提交列表说明。
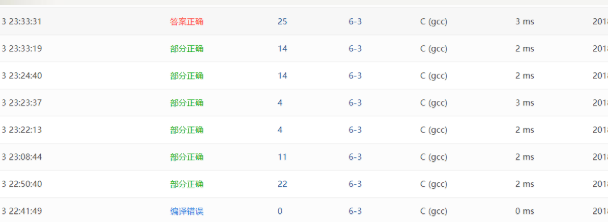
-Q1:老师在课上有讲解如何写,就是利用到了二叉搜索树的性质来解决该问题。
-A1:左子树的结点的值都小于根结点的值,右子树的结点的值都大于根结点的值,判断给出的俩个值是不是一个大于一个小于,如果是则这时的根结点就符合要求。
-Q2:刚开始提交有出现错误,测试点提示不在树中的情况错误,原来是忽略了不在树中情况,后面为了还是用递归的方法。
-A2:添加了一个判断节点是否在树中的find函数,修改完后提交正确。
2.3 题目3:是否二叉搜索树
2.3.1 设计思路
for int j=1 to i
if a[j-1]>=a[j]//如果中序遍历不是升序的,就不是二叉搜索树
return 0;
end for
return 1;
2.3.2 代码截图

2.3.3 PTA提交列表说明。

这题比较容易,编译错误是由于函数复制错了。
思路比较简单,运气也不错一次就过了
3.阅读代码
3.1 题目 (ACM题目已翻译)
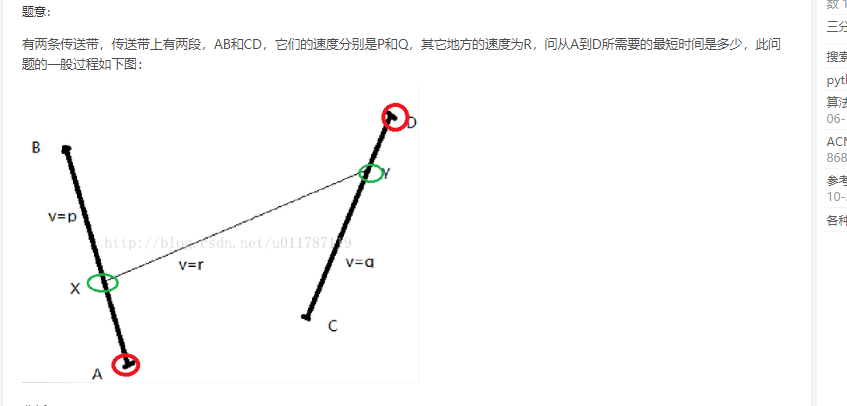
3.2 解题思路

3.3 代码截图

3.4 学习体会
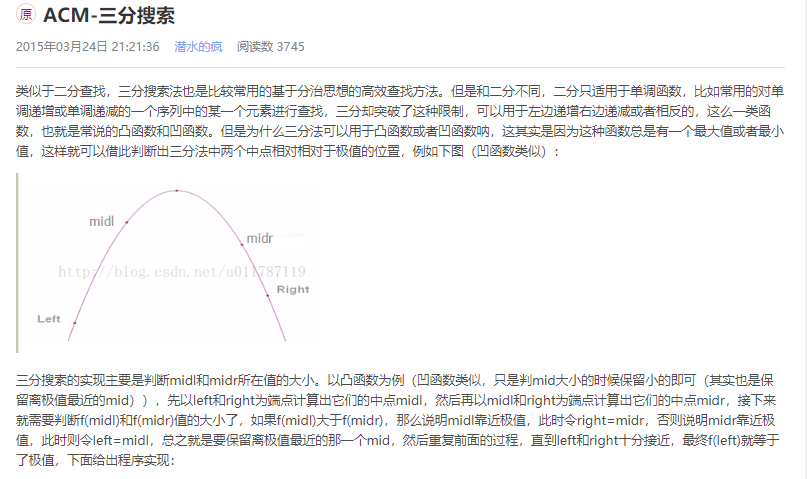
类似于二分查找,三分搜索法也是比较常用的基于分治思想的高效查找方法。但是和二分不同,二分只适用于单调函数,比如常用的对单调递增或单调递减的一个序列中的某一个元素进行查找,三分却突破了这种限制,可以用于左边递增右边递减或者相反的,这么一类函数,也就是常说的凸函数和凹函数。但是为什么三分法可以用于凸函数或者凹函数呐,这其实是因为这种函数总是有一个最大值或者最小值,这样就可以借此判断出三分法中两个中点相对相对于极值的位置,例如下图(凹函数类似):
三分搜索的实现主要是判断midl和midr所在值的大小。以凸函数为例(凹函数类似,只是判mid大小的时候保留小的即可(其实也是保留离极值最近的mid)),先以left和right为端点计算出它们的中点midl,然后再以midl和right为端点计算出它们的中点midr,接下来就需要判断f(midl)和f(midr)值的大小了,如果f(midl)大于f(midr),那么说明midl靠近极值,此时令right=midr,否则说明midr靠近极值,此时则令left=midl,总之就是要保留离极值最近的那一个mid,然后重复前面的过程,直到left和right十分接近,最终f(left)就等于了极值.