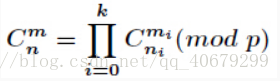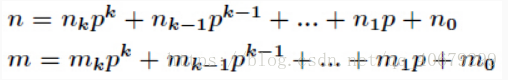并不会证,但总结还是需要的呢。
(Lucus)定理
描述:(公式有点多,还是盗图吧):
其中:
就是个(p)进制下的分解,模拟实现就好了。
数据范围:(1leqslant n,m,pleqslant1×10^5)。
(Q:)定理神奇是挺神奇的,但我们不能直接算吗,复杂度也只是预处理阶乘和逆元,妥妥的过啊?
然后就打了个真·暴力:
(Code):
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int MAXN=1e5+5;
int fac[MAXN],t,m,n,p;
int x,y;
void exgcd(int a,int b)
{
if(b==0)
{
x=1,y=0;
return;
}
exgcd(b,a%b);
int t=x;
x=y;
y=t-a/b*y;
}
int inv(int a,int b){exgcd(a,b);return (x+b)%b;}
void get_fac(int r)
{
fac[0]=fac[1]=1;
for(int i=2;i<=r;i++) fac[i]=1ll*fac[i-1]*i%p;
}
int com(int a,int b)
{
int g=1ll*fac[b]*fac[a-b]%p;
g=inv(g,p);
return 1ll*fac[a]*g%p;
}
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d%d%d",&n,&m,&p);
get_fac(p);
int ans=com(n+m,n)%p;
printf("%d
",ans);
}
return 0;
}
(WA)了之后就去下载数据,然后就是自闭。
请教大佬后知道有时无法得出逆元,如:
[C_{100}^{99};mod;3
]
显然会出锅,这时用(Lucus),避免了这个悲剧(由于(p)进制分解后每项系数都(<p))。
实现方法多样,比如说迭代和递归,然后大佬们全部在线处理阶乘,手玩下发现是对的,难以理解,所以蒟蒻我只能直接离线预处理了(qwq)。
这样的时间复杂度是(O(T(log_pnlog_2n+p)))的,可以通过本题。
下面都有的:
(Code):
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int MAXN=1e5+5;
long long fac[MAXN],t,m,n,p;
long long x,y;
void exgcd(long long a,long long b)
{
if(b==0)
{
x=1,y=0;
return;
}
exgcd(b,a%b);
long long t=x;
x=y;
y=t-a/b*y;
}
long long inv(long long a,long long b){exgcd(a,b);return (x+b)%b;}//逆元
void get_fac(int r)//预处理阶乘
{
fac[0]=fac[1]=1;
for(int i=2;i<=r;i++) fac[i]=fac[i-1]*i%p;
return;
}
long long com(long long a,long long b)//算组合数
{
if(b>a) return 0;
if(a==b) return 1;
if(b>a-b) b=a-b;
//上面是是组合数的性质,保证运算变小的,但是只对在线算法有效,不过你加上也无妨
long long g=fac[b]*fac[a-b]%p;
g=inv(g,p);
return fac[a]*g%p;
}
//迭代实现
/*int lucas(int n,int m,int p)
{
if(m>n) return 0;//迭代的需要注意这个(虽然我不知道为啥)
int ans=1;
while(m)
{
ans=(ans%p*com(n%p,m%p)%p)%p;
n/=p,m/=p;//有一个没了后边就都是不用算了
}
return ans%p;
}*/
//递归实现:
int lucas(int n,int m,int p)
{
if(!m) return 1;
else return (com(n%p,m%p)%p)*(lucas(n/p,m/p,p)%p)%p;
}
int main()
{
scanf("%lld",&t);
while(t--)
{
scanf("%lld%lld%lld",&n,&m,&p);
get_fac(p+1);//+1可以不用
printf("%lld
",lucas(n+m,n,p)%p);
}
return 0;
}
挺神奇的。