题目分别出自:
poj1195,codeforces 482B,codeforces 591A。poj 2503,poj2442,codeforces 445B
A题:
题目描写叙述:
Mobile phones
Write a program, which receives these reports and answers queries about the current total number of active mobile phones in any rectangle-shaped area.

The values will always be in range, so there is no need to check them. In particular, if A is negative, it can be assumed that it will not reduce the square value below zero. The indexing starts at 0, e.g. for a table of size 4 * 4, we have 0 <= X <= 3 and 0 <= Y <= 3.
Table size: 1 * 1 <= S * S <= 1024 * 1024
Cell value V at any time: 0 <= V <= 32767
Update amount: -32768 <= A <= 32767
No of instructions in input: 3 <= U <= 60002
Maximum number of phones in the whole table: M= 2^30
0 4 1 1 2 3 2 0 0 2 2 1 1 1 2 1 1 2 -1 2 1 1 2 3 3
3 4
解析:
A题先晾着。树状数组这一块还没有进行系统的学习。
有兴趣的能够自己做做或者百度一下相关知识学一学。
B题:
题目描写叙述:
Interesting Array
We'll call an array of n non-negative integers a[1], a[2], ..., a[n] interesting,
if it meets m constraints. The i-th of the mconstraints consists of three
integers li, ri, qi (1 ≤ li ≤ ri ≤ n)
meaning that value  should be equal to qi.
should be equal to qi.
Your task is to find any interesting array of n elements or state that such array doesn't exist.
Expression x&y means the bitwise AND of numbers x and y. In programming languages C++, Java and Python this operation is represented as "&", in Pascal — as "and".
The first line contains two integers n, m (1 ≤ n ≤ 105, 1 ≤ m ≤ 105) — the number of elements in the array and the number of limits.
Each of the next m lines contains three integers li, ri, qi (1 ≤ li ≤ ri ≤ n, 0 ≤ qi < 230) describing the i-th limit.
If the interesting array exists, in the first line print "YES" (without the quotes) and in the second line print n integersa[1], a[2], ..., a[n] (0 ≤ a[i] < 230) decribing the interesting array. If there are multiple answers, print any of them.
If the interesting array doesn't exist, print "NO" (without the quotes) in the single line.
3 1
1 3 3
YES
3 3 3
3 2
1 3 3
1 3 2
NO
题意:
给定n,m,分别表示数组a中元素的个数和"限制"的组数,接下来是m组限制,每组限制有三个数据。各自是l,r。p,表示要满
足条件数组a[l] & a[l+1] & ...a[r] = p,然后要求输出满足以上全部m组限制的数组a。假设有多组满足的话,输出随意一组就可以。
解析:
一開始拿到这道题的时候。看到区间问题。立即反应过来要用线段树。
但是想了非常久,依据自己掌握的知识,先要构建一棵线段树,但是题目中却是要输出这种一个数组,意思就是一開始并不提供构建线段树的条件(即数组元素),而是给你一些查询,让你
通过这些查询来输出一棵满足全部查询的树。然后我就纳闷了,去翻了翻当时的官方题解,发现思路很巧妙。题解的思路也就是
将这些查询转换成对应的条件。然后通过这些条件先预处理一棵通过这些条件不断更新后得到的一棵线段树,然后最后再通过这
棵线段树来推断这些条件是否一一成立,若当中有不成立的,说明得到的这棵线段树与已知的查询矛盾。则输出NO。反之则一一
输出线段树中存储的数据元素。即数组元素。
官方题解出处:点击打开链接
完整代码实现:
#include<cstdio>
#include<cstring>
const int MAX_BIT = 29; //表示最大的位数(二进制位)
const int MAX_NUM = (int)1e5 + 10;
const int INF = (1 << 30) - 1; //注意这里的无穷大的取值,不能随便取值
int l[MAX_NUM],r[MAX_NUM],q[MAX_NUM],a[MAX_NUM],sum[MAX_NUM],n,m;
int tree[MAX_NUM * 4];
//数组建立线段树,v为当前遍历到的节点的下标,根节点为1,l,r分别为线段树节点存储的区间的左值和右值
void build(int v,int l,int r){
//遍历到了叶节点
if(l == r){
tree[v] = a[l];
return;
}
int lson = v << 1,rson = lson + 1,mid = (l+r) >> 1;
build(lson,l,mid);
build(rson,mid+1,r);
//节点存储的值为其左右孩子存储的值相与后的结果
tree[v] = tree[lson] & tree[rson];
}
/**v,l,r表示当前遍历到的节点的下标以及存储的左右区间值
**ql,qr表示待查询的区间
*/
int Query(int v, int l, int r, int ql, int qr) {
if (r < ql || l > qr) return INF;
if (ql <= l && r <= qr) return tree[v];
int lson = v<<1, rson = lson+1, mid = (l+r)>>1;
return Query(lson, l, mid, ql, qr) & Query(rson, mid+1, r, ql, qr);
}
void Init(){
scanf("%d %d",&n,&m);
for(int i = 1;i <= m;++i){
scanf("%d %d %d",&l[i],&r[i],&q[i]);
}
for(int i = 0;i <= MAX_BIT;++i){ //考虑q[i]的每一位,假设该位是1。那么数组a[l[i]] —— a[r[i]]相应位均要为1
memset(sum,0,sizeof(sum));
for(int j = 1;j <= m;++j){
if((q[j] >> i) & 1){
++sum[l[j]];
--sum[r[j]+1]; //sum用来标记每次处理的区间
}
}
for(int j = 1;j <= n;++j){
sum[j] += sum[j-1];
if(sum[j] > 0){ //表示处理到的这一位不为0
a[j] |= 1 << i;
}
}
}
build(1,1,n);
}
void solve(){
for(int i = 1;i <= m;++i){
if(Query(1,1,n,l[i],r[i])!=q[i]){
printf("NO
");
return;
}
}
printf("YES
");
for(int i = 1;i <= n;++i){
if(i-1){
printf(" ");
}
printf("%d ",a[i]);
}
printf("
");
}
int main(){
Init();
solve();
return 0;
}这道题目是非常好的题目。感觉自己还不是非常懂,等到过段时间线段树这部分总结了之后一定要再来看看。
C题:
题目描写叙述:
Wizards' Duel
Harry Potter and He-Who-Must-Not-Be-Named engaged in a fight to the death once again. This time they are located at opposite ends of the corridor of length l. Two opponents simultaneously charge a deadly spell in the enemy. We know that the impulse of Harry's magic spell flies at a speed of p meters per second, and the impulse of You-Know-Who's magic spell flies at a speed of q meters per second.
The impulses are moving through the corridor toward each other, and at the time of the collision they turn round and fly back to those who cast them without changing their original speeds. Then, as soon as the impulse gets back to it's caster, the wizard reflects it and sends again towards the enemy, without changing the original speed of the impulse.
Since Harry has perfectly mastered the basics of magic, he knows that after the second collision both impulses will disappear, and a powerful explosion will occur exactly in the place of their collision. However, the young wizard isn't good at math, so he asks you to calculate the distance from his position to the place of the second meeting of the spell impulses, provided that the opponents do not change positions during the whole fight.
The first line of the input contains a single integer l (1 ≤ l ≤ 1 000) — the length of the corridor where the fight takes place.
The second line contains integer p, the third line contains integer q (1 ≤ p, q ≤ 500) — the speeds of magical impulses for Harry Potter and He-Who-Must-Not-Be-Named, respectively.
Print a single real number — the distance from the end of the corridor, where Harry is located, to the place of the second meeting of the spell impulses. Your answer will be considered correct if its absolute or relative error will not exceed10 - 4.
Namely: let's assume that your answer equals a, and the answer of the jury is b. The checker
program will consider your answer correct if 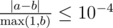 .
.
100
50
50
50
199
60
40
119.4
NoteIn the first sample the speeds of the impulses are equal, so both of their meetings occur exactly in the middle of the corridor.
题意:
Harry 和 He-Who-Must-Not-Be-Named 分别在走廊末端,各发射自己的impulse,当中Harry 的 impulse 速度为 p 米/s。He-Who-
Must-Not-Be-Named为 q米/s。
然后相遇之后各自回到它们的主人身边。再发射。再发射时的速度保持不变。问第二次相遇的时候。
Harry的impulse 离他的位置距离是多少。
解析:
因为第二次再发射的时候速度保持不变。因此相遇点仍然是第一次相遇的那个点。
因此得出一元一次方程(p+q)* t = l;
然后再p*t则是全部答案。
完整代码实现:
#include<cstdio>
int main(){
int l,p,q;
scanf("%d %d %d",&l,&p,&q);
printf("%.6f
",(double)l/(p+q)*p);
}D题:
题目描写叙述:
Babelfish
dog ogday cat atcay pig igpay froot ootfray loops oopslay atcay ittenkay oopslay
cat eh loops
在词典中,给定一些翻译后的单词及翻译前的单词,然后空行隔开,再给定一些翻译前的单词。假设这些翻译前的单词存在词
典中,那么输出其翻译后的单词,否则的话,则输出字符串eh。
解析:
这道题因为数据量很大。词典中最多高达10^5组单词,并且查询次数也达到了10^5次方,因此暴力遍历的方法显然是不可行
的,因为这道题的时限比較宽松。因此用映射容器map也能过。注意空行的处理,在这里空行仅仅有一个' '字符。
完整代码实现:
#include<iostream>
#include<algorithm>
#include<string>
#include<map>
#include<cstring>
#include<cstdio>
using namespace std;
map <string,string> mp;
int main(){
char temp[50];
string str,str1,str2;
while(gets(temp) && strlen(temp)){
for(int j = 0;;++j){
if(temp[j]==' '){
temp[j] = '�';
str1 = temp;
str2 = temp+j+1;
break;
}
}
mp[str2] = str1;
}
while(cin >> str){
if(mp[str].size()){
cout << mp[str] << endl;
}
else{
cout << "eh" << endl;
}
}
return 0;
}
假设这道题时限改成1s的话。那么这样做必定就超时了。因此引入了字典树的做法,因为字典树我还没有进行比較系统的学习,所
以这里就贴上黄种枝学长的字典树代码:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <queue>
#include <string>
#include <set>
#include <stack>
#include <map>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
//数组字典树
#define maxnode 500005
#define sigma_size 26
struct Trie{
int ch[maxnode][sigma_size]; //字典树
int val[maxnode]; //结点信息
int sz; //结点总数
char v[500005][15];
Trie(){sz=1;memset(ch[0],0,sizeof(ch[0]));memset(val,0,sizeof(val));} //字典树初始化
int idx(char c){return c-'a';} //类型转换
//插入字符串s,附加信息v;注意v必须为非0,0代表本节点不是单词结点
void Insert(char *s,char s2[])
{
int u=0,n=strlen(s);
for(int i=0;i<n;i++)
{
int c=idx(s[i]);
if(!ch[u][c])
{
memset(ch[sz],0,sizeof(ch[sz]));
//val[sz]=0; //中间附加信息0
ch[u][c]=sz++;
}
u=ch[u][c]; //往下走
}
val[u]=1; //单词结尾附加信息v
n=strlen(s2);
for(int j=0;j<=n;j++)
v[u][j]=s2[j];
}
void Find(char *s){
int u=0,n=strlen(s),i=0;
for(;i<n;i++)
{
int c=idx(s[i]);
u=ch[u][c]; //往下走
if(u==0){
break;
}
}
if(i==n&&val[u]==1){
printf("%s
",v[u]);
}else
printf("eh
");
}
};
Trie T;
int main()
{
char s1[1000],s2[1000];
char c;
while(scanf("%s",s1)!=EOF){
c=getchar();
if(c==10){
T.Find(s1);
}
else if(c==32){
scanf("%s",s2);
T.Insert(s2,s1);
}
}
return 0;
}E题:
题目描写叙述:
Sequence
1 2 3 1 2 3 2 2 3
3 3 4
题意:
给定一个数T,表示有T组測试数据。接下来一行的两个数各自是m和n。然后是一个m*n的矩阵(m行n列),问从这m行中,每行取一个数,组成一个新
的数列a,显然这种数列能够取n^m种,问在这n^m种数列中,找出数列和前n小的数列,并输出它们的和。
解析:这道题的思路比較巧妙,借鉴了一下别人的解题思路:
显然要得到和前n小的数列,非常easy想到用堆或者优先队列的方式来维护前n小,那么一開始的时候我们先输入第一行数据,将其升序排序之后,排序后的数列为num1[0...n-1]。然后输入第二行数据,因为要得到的是前n小和的数列,那么第二行数据也对其进
行升序排序,排序后的数列为num2[0...n-1],然后我们将因为要得到前n小和的数列,因此一開始的时候。我们将num2[0]分别于
num1[0...n-1]相加。并一一压入优先队列(大顶堆)中,然后再考虑num2[1]与num1[0...n-1]相加,假设顺序相加时num2[1] + num1[i]
比堆顶元素小,那么就要删除堆顶元素了(说明此时优先队列中的堆顶元素不属于前n小),然后再将num2[1] + num1[i]压入队列中,
假设顺序相加时num2[1] + num1[i]比堆顶元素大,那么跳出循环体,继续依照相同的方式考虑num2[2]与num1[0...n-1]相加后的结
果,直到第二行的数据处理完成之后,将优先队列中的元素赋值给num1数组,并清空优先队列,然后再循环上述步骤,直到全部数
据都处理完成。
最后输出的时候。注意特判仅仅有一行元素的情况,应该正序输出
完整代码实现:
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
const int MAX_N = int(2e3) + 10;
int num1[MAX_N],num2[MAX_N];
template<class T>
inline bool In(T &n)
{
T x = 0, tmp = 1; char c = getchar();
while((c < '0' || c > '9') && c != '-' && c != EOF) c = getchar();
if(c == EOF) return false;
if(c == '-') c = getchar(), tmp = -1;
while(c >= '0' && c <= '9') x *= 10, x += (c - '0'),c = getchar();
n = x*tmp;
return true;
}
template<class T>
inline void Out(T n)
{
if(n < 0)
{
putchar('-');
n = -n;
}
int len = 0,data[20];
while(n)
{
data[len++] = n%10;
n /= 10;
}
if(!len) data[len++] = 0;
while(len--) putchar(data[len]+48);
}
/**切割线**/
void solve(){
int T,m,n;
scanf("%d",&T);
while(T--){
priority_queue <int> que; //默觉得大顶堆
In(m);
In(n);
for(int i = 0;i < n;++i){
In(num1[i]);
}
sort(num1,num1+n);
for(int i = 1;i < m;++i){
sort(num1,num1+n);
for(int j = 0;j < n;++j){
In(num2[j]);
}
sort(num2,num2+n);
for(int j = 0;j < n;++j){
que.push(num2[0]+num1[j]);
}
for(int j = 1;j < n;++j){
for(int k = 0;k < n;++k){
if((num2[j] + num1[k]) < que.top()){
que.pop();
que.push(num2[j] + num1[k]);
}
else{
break;
}
}
}
int j = 0;
while(!que.empty()){
num1[j] = que.top();
que.pop();
++j;
}
}
if(m == 1){
for(int j = 0;j < n;++j){
if(j){
printf(" ");
Out(num1[j]);
}
else{
Out(num1[j]);
}
}
printf("
");
}
else{
for(int j = n-1;j >= 0;--j){
if(j){
Out(num1[j]);
printf(" ");
}
else{
Out(num1[j]);
printf("
");
}
}
}
}
}
int main(){
solve();
return 0;
}附上收集到的一些測试数据:
3 4 1 2 3 4 1 2 3 4 1 2 3 4 正确输出 3 4 4 4 1 10 10 21 12 123 3 21 123 32 143 43 56 2 32 43 34 54 56 656 76 43 234 234 45 5 65 56 76 43 23 435 57 32 324 435 46 56 76 87 78 43 23 3 32 324 45 56 57 34 23 54 565 23 32 34 342 324 232 2 432 324 12 234 324 4 45 65 67 435 23 5 654 34 3245 345 56 56 657 67 456 345 325 234 234 546 65 88 66 53 654 65 765 5 3 34 34 34 56 345 234 2 34 正确输出 131 132 132 133 134 135 140 140 141 141 特判数据是一行的情况 1 1 5 1 2 3 4 5 正确输出:1 2 3 4 5
F题:
题目描写叙述:
DZY Loves Chemistry
DZY loves chemistry, and he enjoys mixing chemicals.
DZY has n chemicals, and m pairs of them will react. He wants to pour these chemicals into a test tube, and he needs to pour them in one by one, in any order.
Let's consider the danger of a test tube. Danger of an empty test tube is 1. And every time when DZY pours a chemical, if there are already one or more chemicals in the test tube that can react with it, the danger of the test tube will be multiplied by 2. Otherwise the danger remains as it is.
Find the maximum possible danger after pouring all the chemicals one by one in optimal order.
The first line contains two space-separated integers n and m 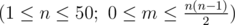 .
.
Each of the next m lines contains two space-separated integers xi and yi (1 ≤ xi < yi ≤ n). These integers mean that the chemical xi will react with the chemical yi. Each pair of chemicals will appear at most once in the input.
Consider all the chemicals numbered from 1 to n in some order.
Print a single integer — the maximum possible danger.
1 0
1
2 1
1 2
2
3 2
1 2
2 3
4
NoteIn the first sample, there's only one way to pour, and the danger won't increase.
In the second sample, no matter we pour the 1st chemical first, or pour the 2nd chemical first, the answer is always 2.
In the third sample, there are four ways to achieve the maximum possible danger: 2-1-3, 2-3-1, 1-2-3 and 3-2-1 (that is the numbers of the chemicals in order of pouring).
给定n种元素,然后再给定m种组合。每种表示表示这两种元素会发生反应。然后再给定一根试管。试管最初的危急系数为1,
然后依照一定的顺序将这n种元素倒入试管中,在倒入某种元素时,假设试管中存在着与之能发生反应的元素。那么试管的危急系数
则在原来的基础上*2,要求输出的是,依照某种顺序将元素倒入试管中后,试管的危急系数最大。并输出该危急系数。
解析:
刚開始拿到这道题的时候,非常明显感觉到这是一道并查集的题目。可是要得到题目要求还是不太清楚,因此我们考虑一些特殊
的数据,从中总结出一般规律:
比如:
6 4
1 2
2 3
4 5
5 6
非常明显,我们能够将这6种元素分为2类,一类是{1,2,3},另外一类是{4,5,6}
那么,我们在将元素倒入试管中时,先将哪一类倒入试管中对最后的结果并不会有影响。
因此一開始的时候我们倒入第一类,以1 — 2 — 3的顺序倒入(注意不得随便调换顺序。比方说假设依照1-3-2的顺序倒入则无法使危
险系数最大),此时危急系数为4,然后開始考虑第二类,发现无论是4,5,6中的哪一种先倒入。都不能与试管中已有的元素反应,因
为这是属于两个不相交集合(也能够是说是属于两棵有根树的不同节点),然后我们将第二类依照4 — 5 — 6的顺序倒入。倒入4的时
候。危急系数不翻倍,倒入5的时候,由于里面已经有了4元素,能和元素5反应,因此危急系数翻倍,元素6同理。因此在所有元素
全然倒入之后,危急系数变为2^2 * 2^2 = 2^4。也就是2^(n - a)。a为这些元素可以分成多少类。
因此有了以上的分析之后,我们得出结论。用并查集先将这些属于同一有根树的元素归类,然后每棵有根树依照最佳的顺序倒入试
管中(每棵有根树是独立的)。然后当处理完一棵有根树之后,要处理另外一棵有根树的话。第一个放入的元素是不会使危急系数翻倍
的。即全部有根树第一个元素放入试管中时,试管危急系数均不翻倍。那么我们须要求的即是有根树的数量了,也就是连通分量的
个数,然后将总结点数减去连通分量个数,再作为2的幂指数即得最后的危急系数。
完整代码实现:
#include<cstdio>
#include<cmath>
const int MAX_N = 100;
int father[MAX_N],sum;
int find_set(int node) {
if (father[node] != node){
father[node] = find_set(father[node]);
}
return father[node];
}
void _union(int p,int q){
int root1 = find_set(p);
int root2 = find_set(q);
if(root1==root2){
return;
}
father[root2] = root1;
--sum;
}
void solve(){
int n,m,x,y,root;
scanf("%d %d",&n,&m);
for(int i = 1;i <= n;++i){
father[i] = i;
}
sum = n;
for(int i = 1;i <= m;++i){
scanf("%d %d",&x,&y);
_union(x,y);
}
printf("%I64d
",(long long)(pow(2,n-sum)));
}
int main(){
solve();
return 0;
}周赛总结:做过的题目或者学习过的知识点,过段时间一定要回想一遍,这样才干慢慢的让这些东西属于自己。临时不懂的
题目。或者题解都看不懂的题目,先放一放,等到认为自己有了这方面的知识基础之后。再来看一看。