回顾数学期望和方差的公式:
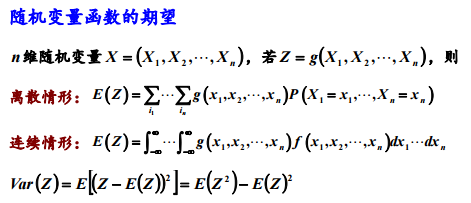
1. 多元随机变量更本质的方面是各分量之间的相互关系、相互作用,这方面最重要的数 字特征是协方差与相关系数。
公式: Cov(X,Y) = E(X-E(X))-E(Y-E(Y))。
当X,Y相互独立,Cov(X,Y)=0。协方差就是研究当X,Y不相互独立的时候。随机变量间的相互关系及作用。
协方差的意义:表示X,Y之间存在的关系,及其密切程度。
2. 协方差的性质:

3. 随机变量X,Y的相关系数
单位化:kX与kY(向量X,Y被线性拉伸)是无法判断相关性的,所以
![]()
4. 协方差矩阵:
https://blog.csdn.net/qq_23100417/article/details/84935692
协方差矩阵求法
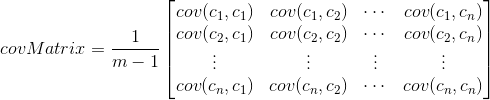
协方差的意义
X和Y的协方差不为0的时候,表明X和Y是相关的,当COV(X,Y)>0的时候,X增大时Y也增大,X减小,Y也减小;;COV(X,Y)<0时,X增大则Y减小,X减小则Y增大。
条件异方差:
Var(Epsilon_i | X) = Sigma_i平方 矩阵,只有主对角线上的Sigma_i平方,其他都是0。因为EPS_i 与 EPS_j 是不相关的。
9.2 协方差
2.1 协方差定义,意义及其性质
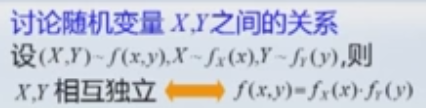
当X与Y的随机变量相互独立,f(x,y)=f(x)*f(y),即联合密度=两个密度的乘积。




多元随机变量更本质的方面是各分量之间的相互关系、相互作用,这方面最重要的数 字特征是协方差与相关系数。
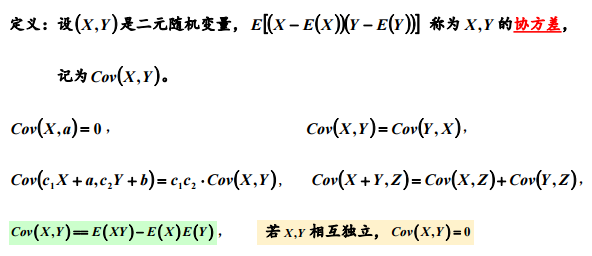

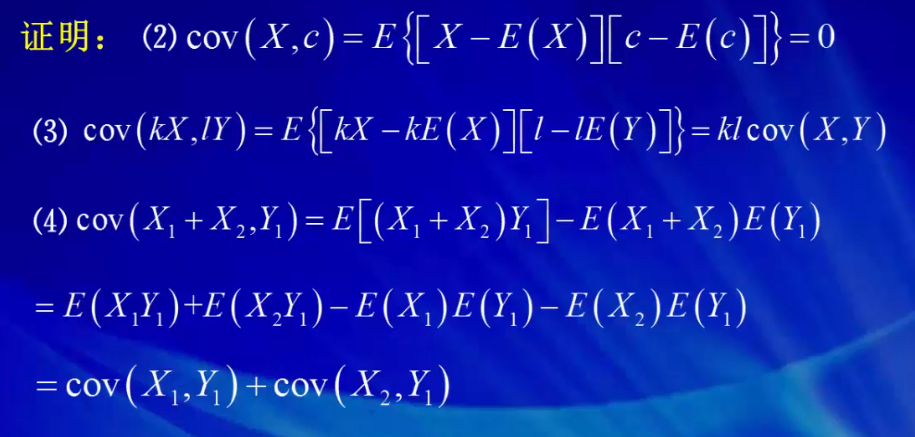
2)X.Y的协方差是可交换的。
3)若Y=X,D(X) = E(X-E(X))^2 = Cov(X,Y) =>协方差是方差的概念的推广。
(4) cov(X1+X2,Y) = E[(X1+X2)*Y - (X1+X2)*E(Y) - E(X1+E2)*Y +E(X1+X2)*E(Y)] = E(X1*Y)+E(X2*Y)-E(X1)*E(Y) -E(X2)*E(Y) = Cov(X1,Y) + Cov(X2,Y), 其中 E(E(X)) = C = E(X), 所以E(X1+X2)*E(Y) - E[(x1+x2)*Y) =0。 Cov(X,Y)=E(XY)-E(X)*E(Y)
2.2 例子





2.3 相关系数


Cov(kX,kY)=K^2Cov(X,Y) 仅仅表示当它是非零的时候表示X,Y之间的关系,但不能够通过这个协方差的值的大小来刻画这个关系的密切程度。
随机变量乘以一个常数是将这个变量进行拉伸,拉伸后是不能。为了克服这个缺点,就是需要单位化:要考虑2个随机变量的关系的时候,首先进行单位化,即将X减去X的期望除以标准差。
单位化后,把一个随机变量做一个线性变换,使得它的数学期望变为0,方差都是1。

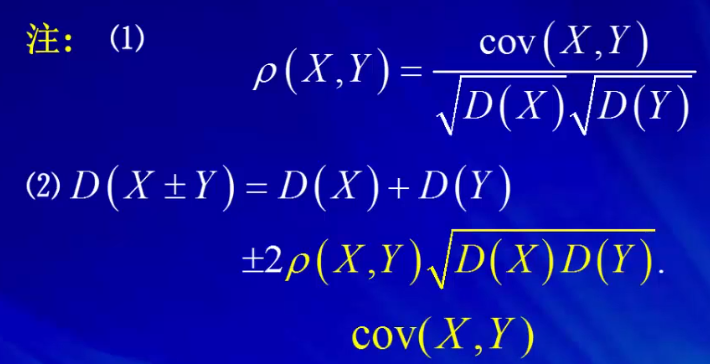
![]()




当Pxy=1时,X与Y正相关,推出X与Y是一条直线,为正相关。
当Pxy=-1时,X与Y负相关,推出X与Y是一条直线,为负相关。
当0<Pxy<1时,X与Y弱相关,
不相关,毛笔画过水面形成一个带状
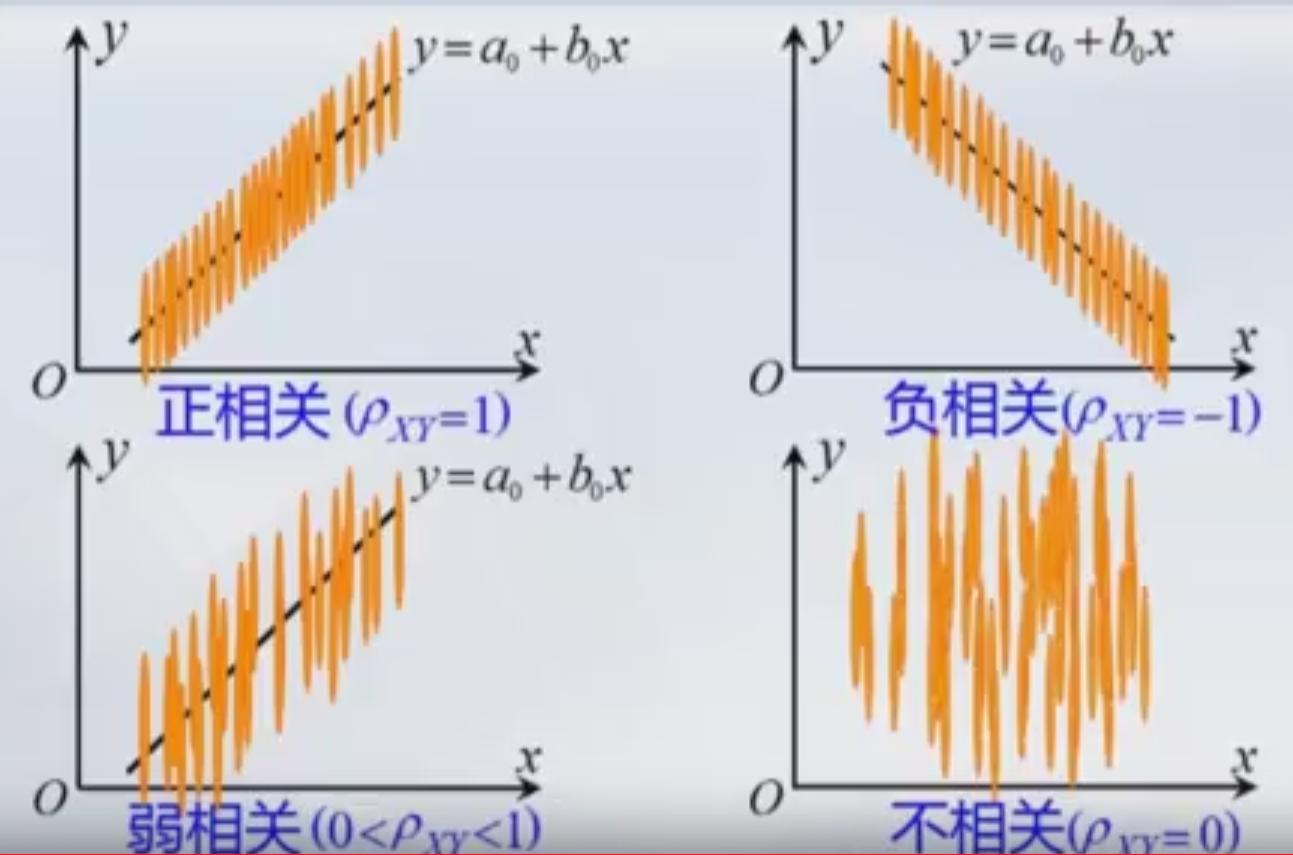



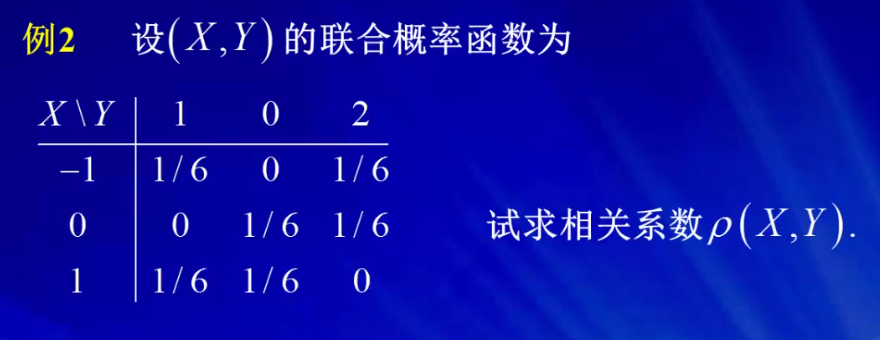
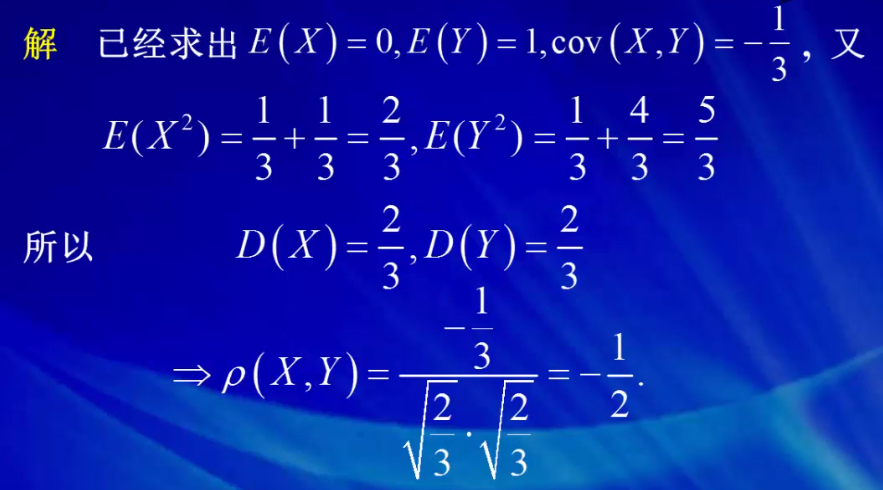
相关系数的性质:



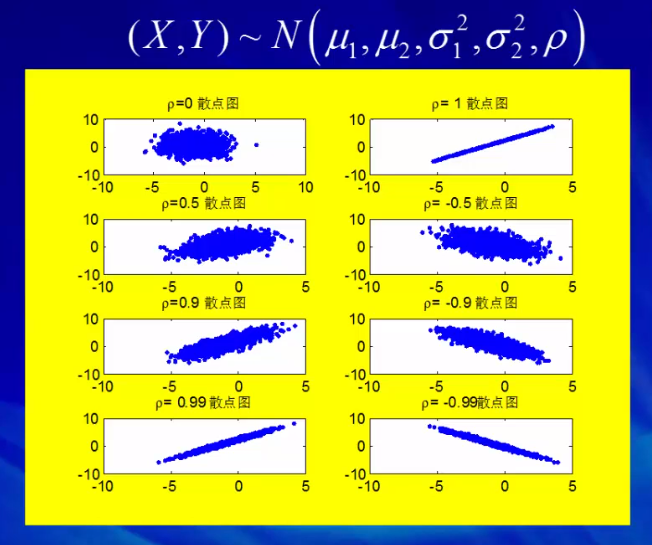



单位圆上的2各点落在圆上的等可能的,所以他们没有线性关系,即线性无关。