4.1 n维向量:元素、集合、关系、结构
元素:n维向量,即n元有序数组
集合:n维向量空间
关系:n维向量的线性运算和线性组合
结构:n维向量的子空间
线性代数核心:线性方程组、矩阵。
- 矩阵的运算与向量的线性运算是一致的。
- 求线性组合的系数等于解方程组。







4.2 向量组线性相关与线性无关
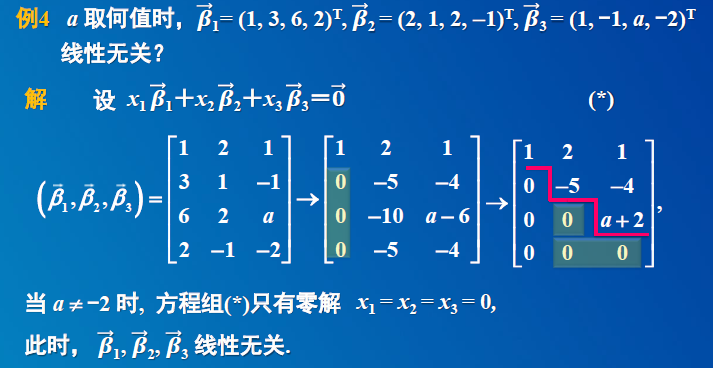
1)判断是否线性相关


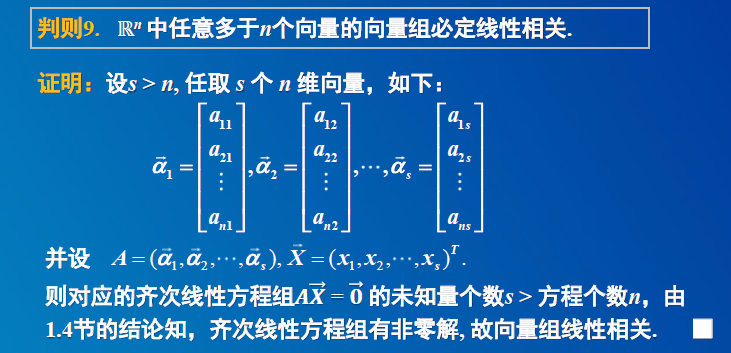
线性是否相关,即线性方程是否有解。




4.3 线性相关性
1)线性相关性的增减关系





2)线性相关性的表出关系



3) 线性相关性的临界关系



4.4 极大线性无关组

1)两个向量组的线性关系




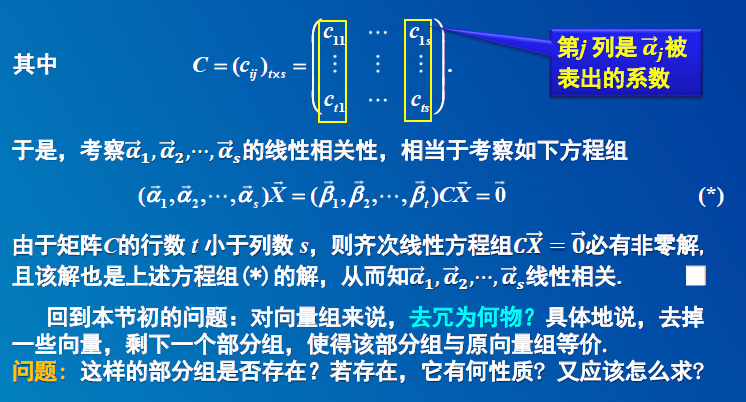
2)极大无关组及其性质


![]()
![]()


3) 极大无关组的求法


4.5 向量的秩

1) 向量组的秩及其性质


![]()
2)向量(子)空间的基与维数

3)矩阵的行秩与列秩


4.6 矩阵的秩

1) 矩阵的k 阶子式

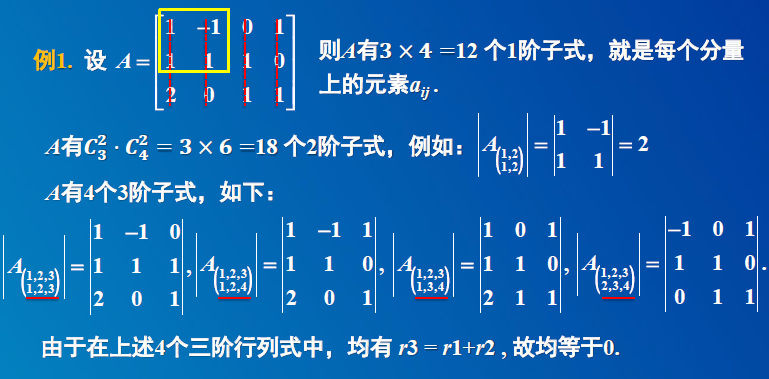
2)矩阵的秩的定义


4.1 n维向量及其运算







