1. 矩阵的线性运算:

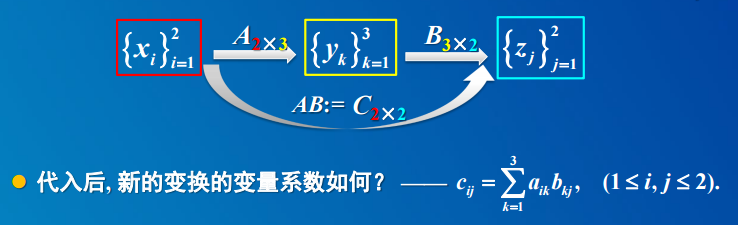
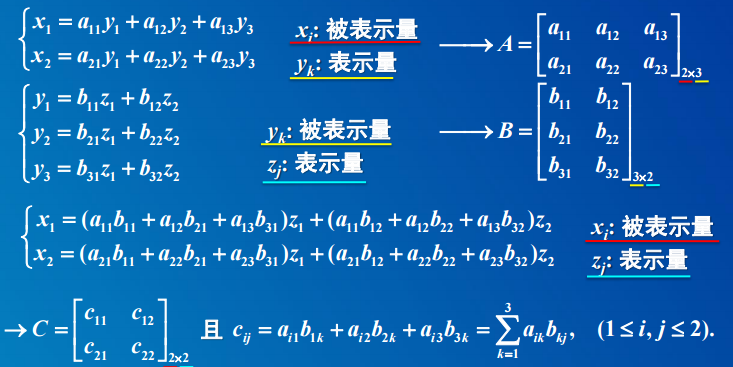
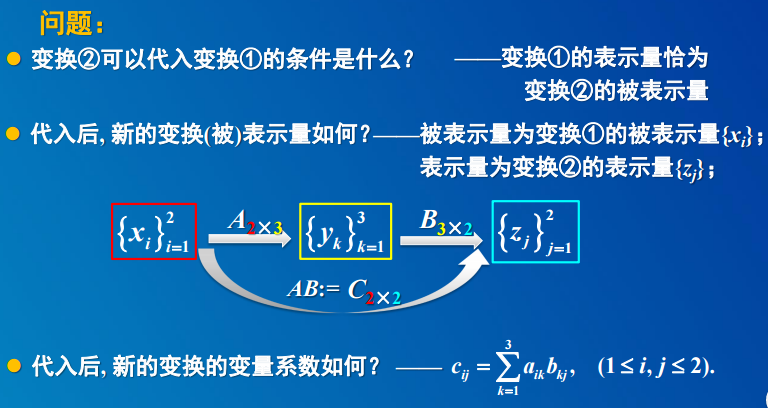
2.1 矩阵的乘法:Xik * Ykj = Zij
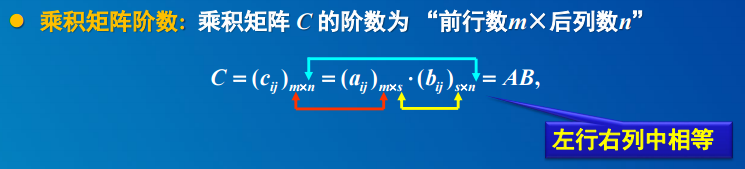
2.2 矩阵乘法性质:

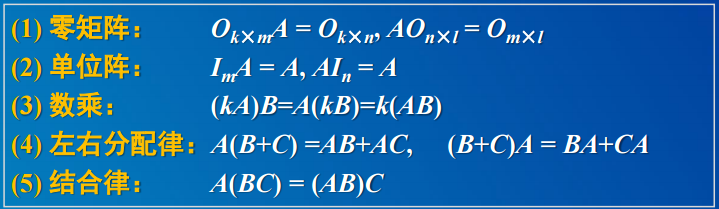
3.1 矩阵的幂次方运算

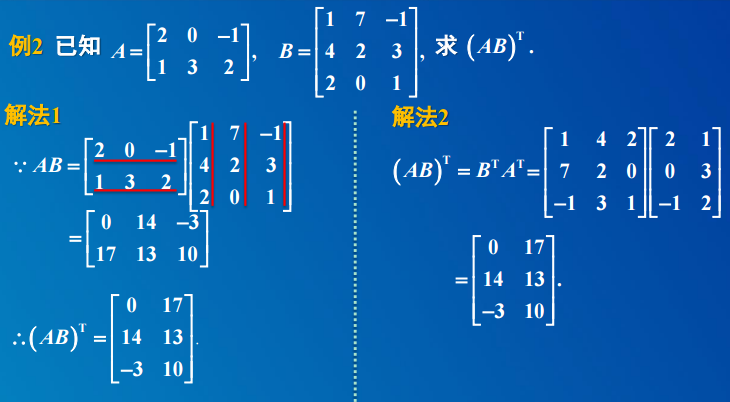
3.2 矩阵转置的运算律

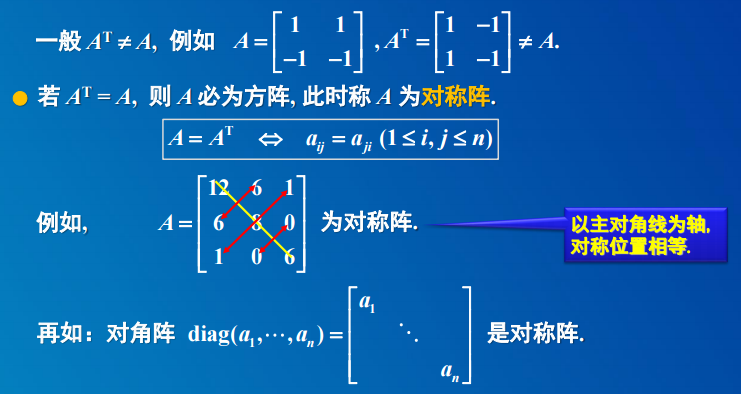
3.3 方阵运算

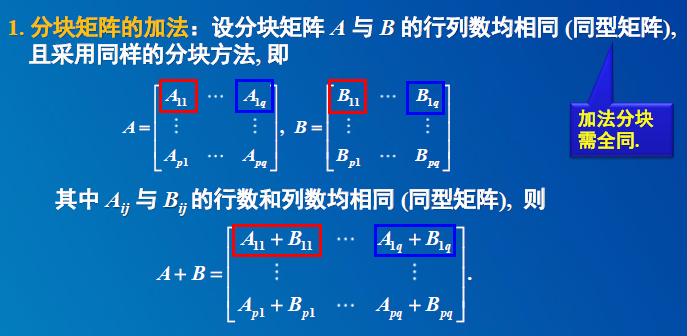
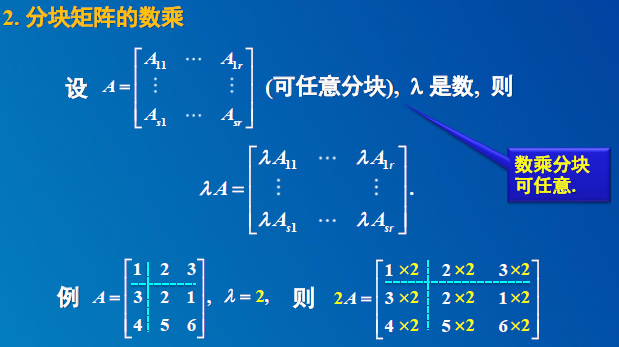
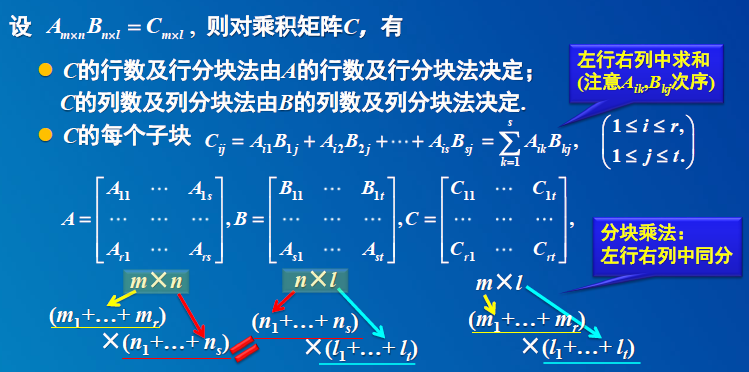
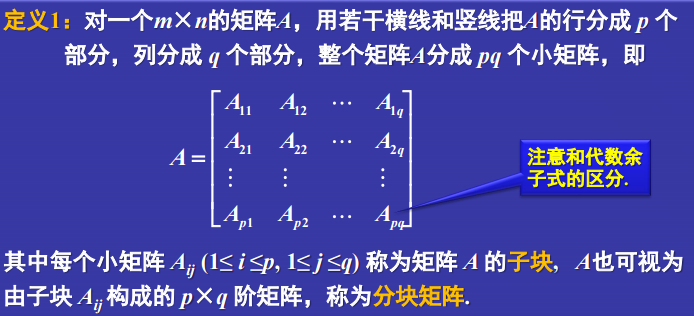
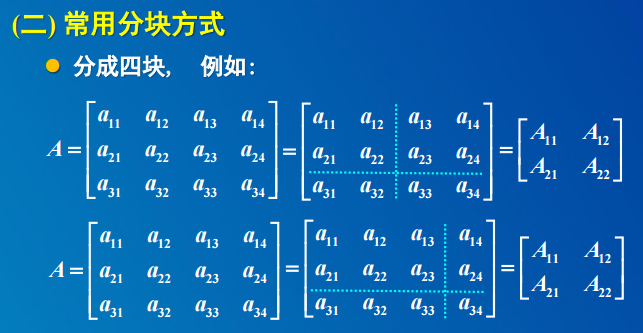
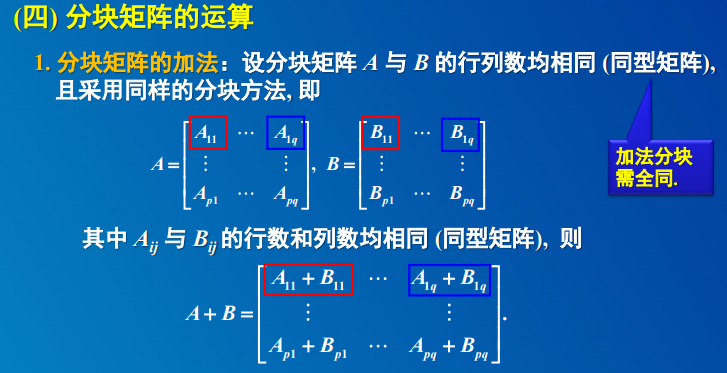
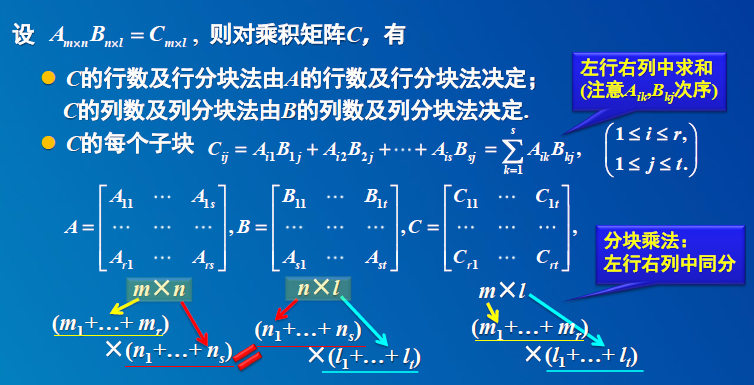
4 分块矩阵的运算


5. 矩阵的初等变换

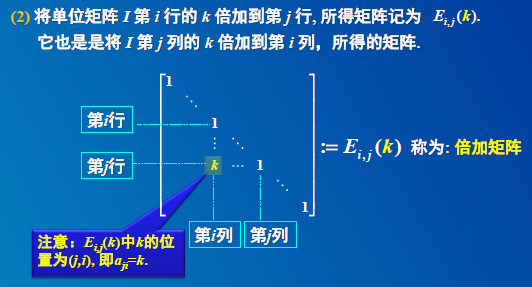
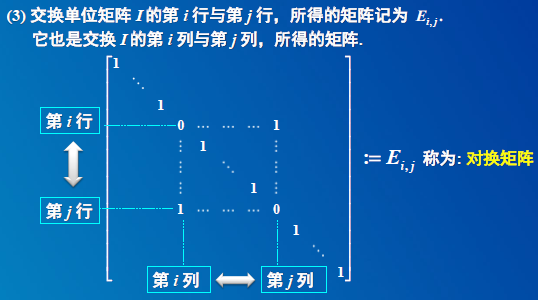
5.1 单位矩阵I经过一次初等变换所得到的矩阵称为初等矩阵.

5.2 初等矩阵的性质:
1) 倍乘矩阵、对换矩阵转置不变(对称阵),转置后仍为初等矩阵
2)|Ei(k)|=k !=0; |Ei,j(k)|=1.
5.3 初等矩阵与初等变换的关系:
1)矩阵A左乘倍乘矩阵 Ei(k),即Ei(k)A,相当于对 A的第 i行做k倍的倍乘变换。矩阵A右乘倍乘矩阵 Ei(k),相当于对 A的第 i列做k倍的倍乘变换。


2)矩阵A左乘对换矩阵 Ei,j,相当于对 A的第 i, j 行做对换变换. 矩阵A右乘对换矩阵 Ej,i,相当于对 A的第 i, j 列做对换变。
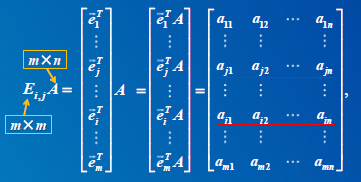

3)矩阵A左乘倍加矩阵Ei,j(k),相当于对A做第i 行的k倍加到第j 行上的倍加变换。 矩阵A右乘倍加矩阵Ei,j(k),相当于对A做第j 列的k倍加到第i 列上的倍加变换.

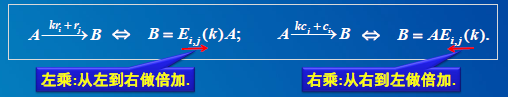

6. 逆矩阵
6.1 定义:设A为n阶方阵, 若存在n阶方阵B, 使得AB = BA = In, 则称A为可逆矩阵或非奇异矩阵, 而称B 为A 的逆矩阵,并记为A-1.
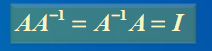
6.2 逆矩阵的性质:

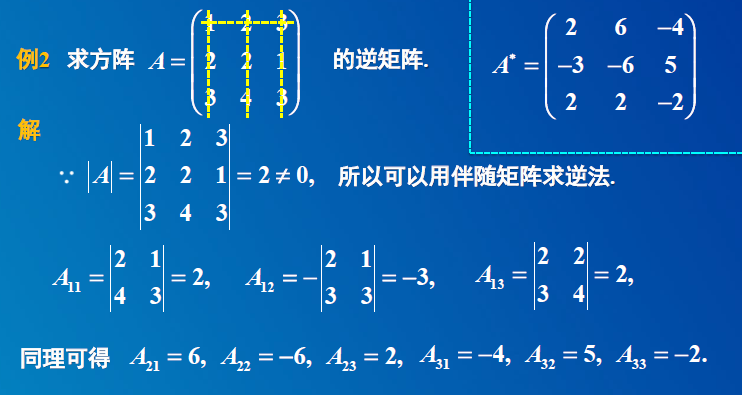
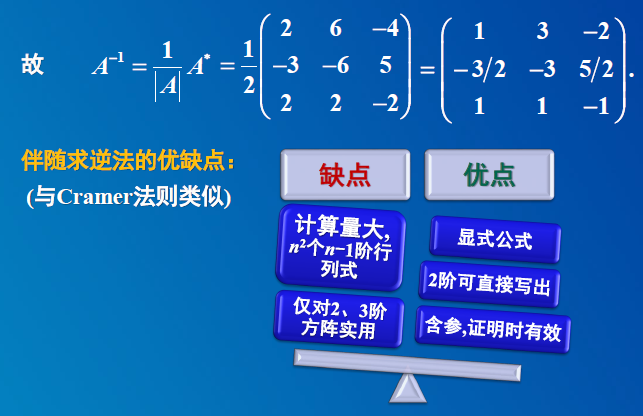
6.3 伴随矩阵


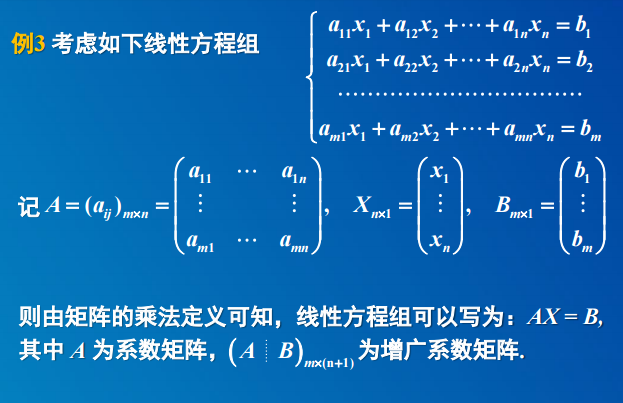
1. 矩阵及其运算




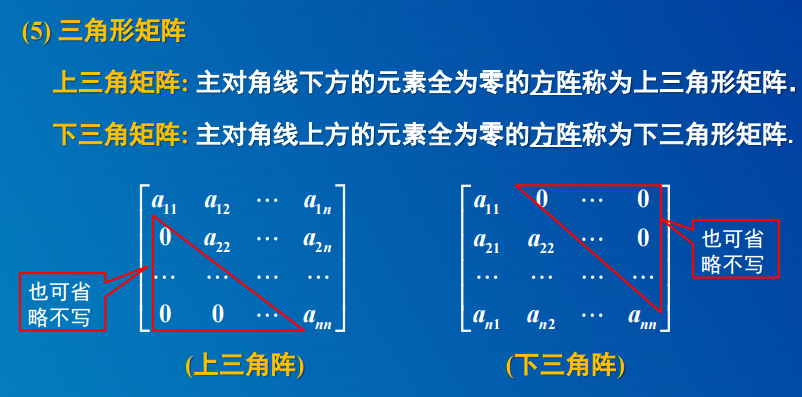

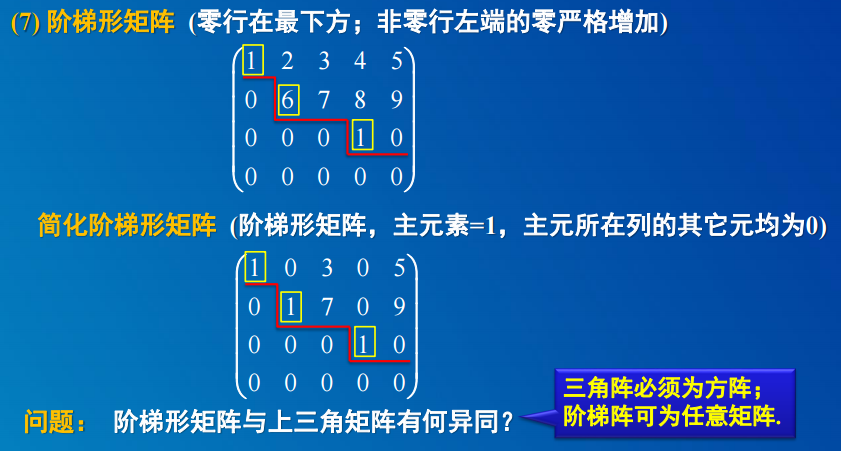
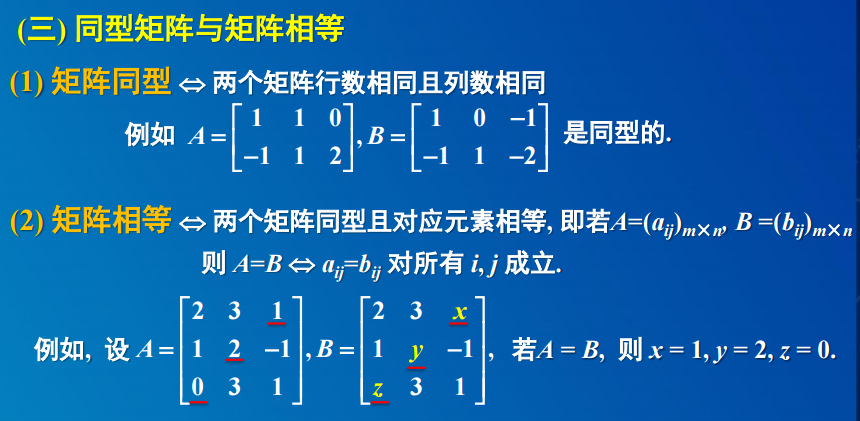




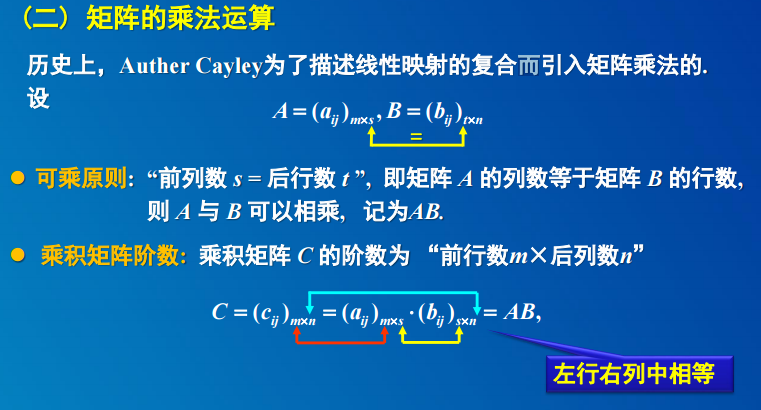
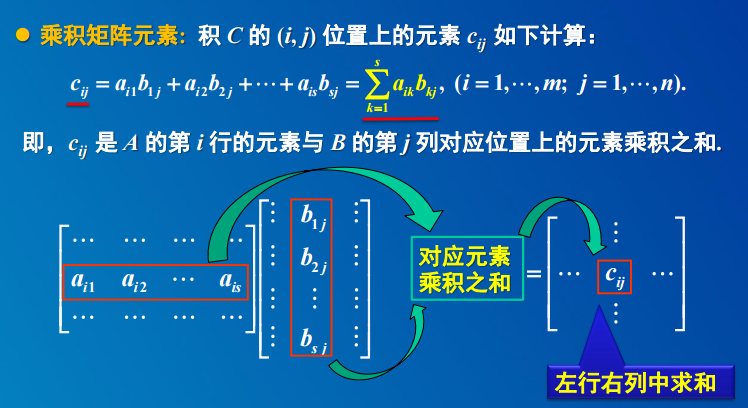
2. 矩阵的乘法运算

被表示量x_i正好对应了这个矩阵A的行数,而表示量y_k的个数正好对应了矩阵A的列数。

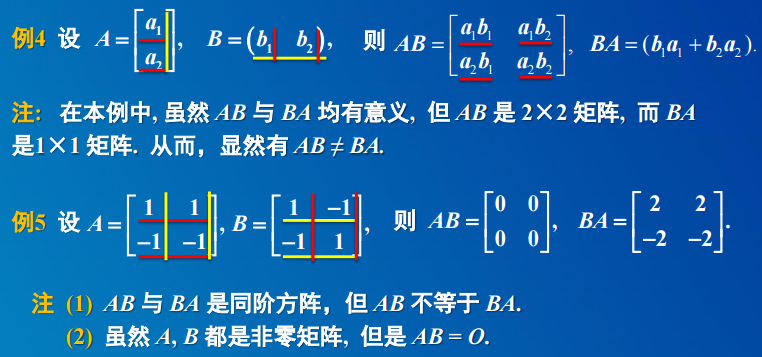



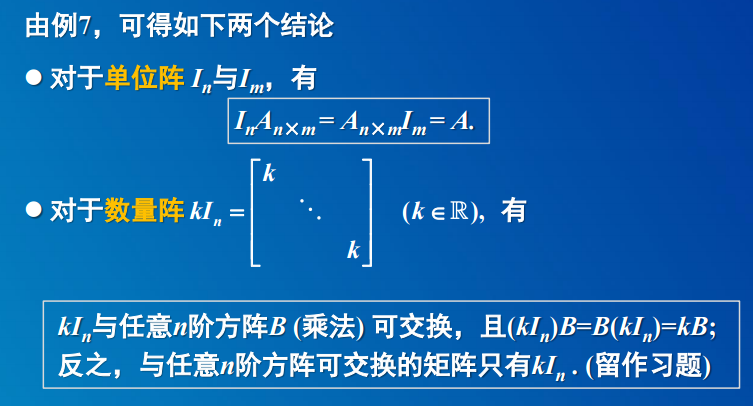


3.3 矩阵的其它运算



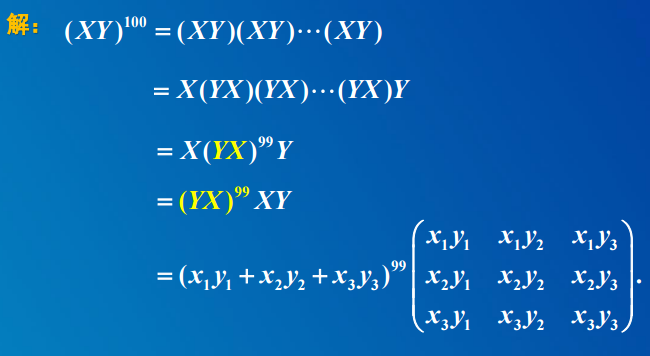










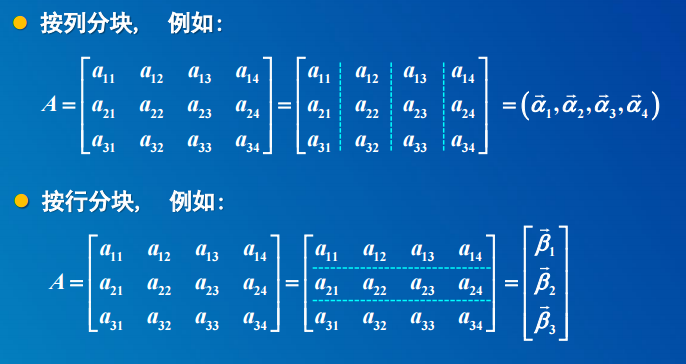
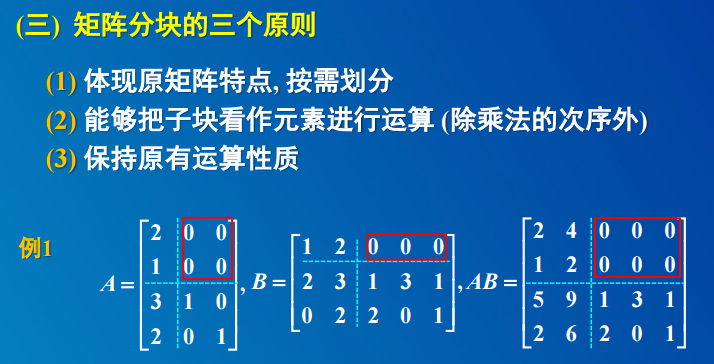
4. 分块矩阵




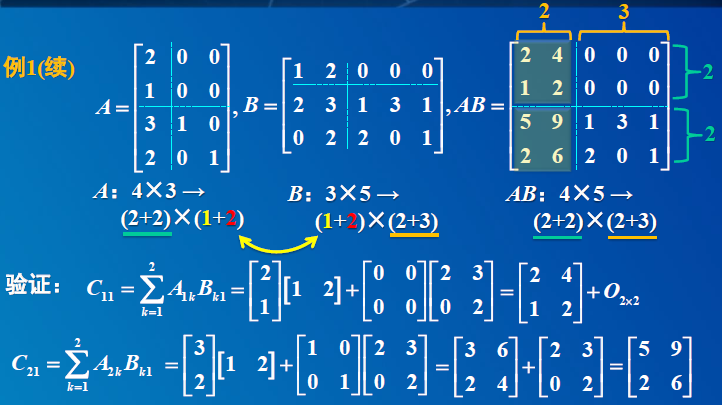
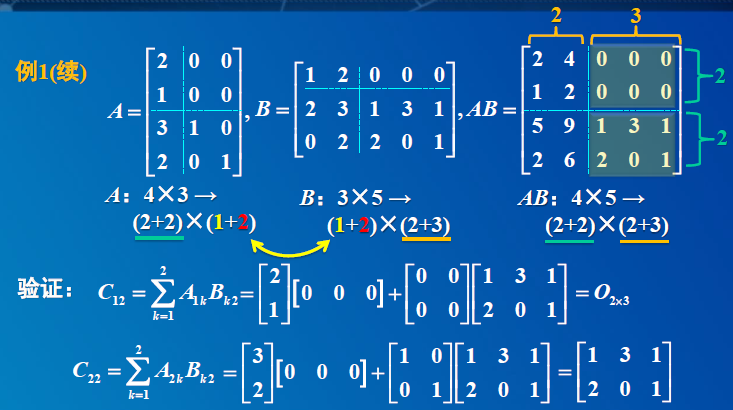

5. 初等矩阵
