山东大学——线性代数:
http://www.xuetangx.com/courses/course-v1:SDUx+00931800X+sp/courseware/45412e228fef48e08a937bdebd19a5a0/61676d9b49ce410290738e6bbc5ed468/
1. 相似矩阵的简单性质: B=P-1AP.
- A~B => r(A)=r(B)
- A~B => |A|=|B|
- A~B => A-1= B-1
- A~B => f(A)=f(B)
相似矩阵的简单应用:A~B => Ak = (P-1BP)k=(P-1BkP)直接做A的k次幂比较难做,而做A的相似矩阵对角阵的k次幂相对更简单。
2. 特征值和特征向量求法的步骤:

3. 特征值和特征向量的性质
- 性质1. n阶矩阵A的相异特征值λ1、λ2、...、λm所对应的特征向量ξ1、ξ2、...、ξm线性无关。
- 性质2:相似矩阵有相同的特征值。A~B => |A-λE|= |B-λE|
4. 矩阵相似对角化的步骤:

一般矩阵对角化的问题,当他有重特征值的时候要判断一下它矩阵的秩,然后,当它与对角阵相似的时候,把它所有的特征值和特征向量求出来,所有特征向量组成了P,所有特征值组成Λ。
一、矩阵的相似

1.1 矩阵的相似定义

自反性:自己跟自己相似,相似变换矩阵E(单位阵)。
对称性:A和B相似,B与A也相似,相似变换矩阵P-1
传递性:A与B相似,B与C相似,则A与C相似。

B= P1-1AP1 => C = P2-1BP2 = P2-1P1-1AP1 P2
所以A与C的相似变换矩阵式P1 P2
2)相似可以推出等价,而等价不能推出相似。

相似矩阵的秩是相同的。
1.2 相似矩阵的简单性质

2)方阵的行列式等于行列式的乘积。P的行列式与P逆行列式的倒数。

3)A=P-1BP => A-1 = P-1B-1 p

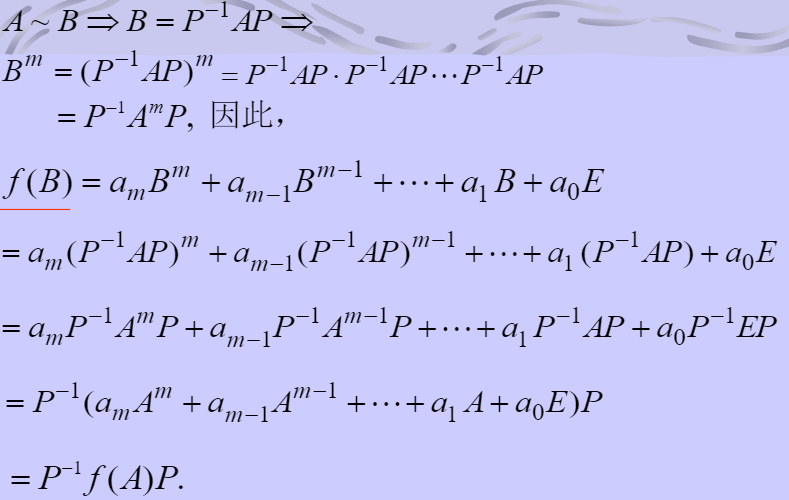
1.3 相似矩阵的简单应用

直接做A的k次幂比较难做,而做A的相似矩阵对角阵的k次幂相对更简单。

将P矩阵拆开,再分别与A矩阵相乘。得到了4与-2,及P矩阵。
而(1,2)矩阵就不能与A(1,2)相乘后的矩阵(5,3)线性相关。
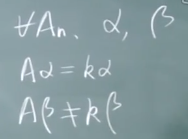
任意给定A,Apha,Beta,Aa=ka,而ABeta != kBeta
A与a相乘后,新向量与原来向量有线性关系。
2.1 特征值和特征向量

求特征向量,就是将A乘以a。

求特征值,A*a=λ*a => (A-λE) *a=0,也就是求齐次性方程组(A-λE)=0有没有非0解。

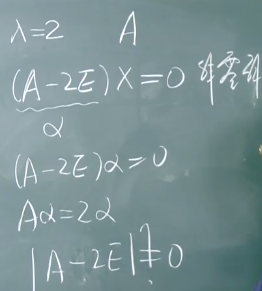
二、特征值与特征向量的求法



试根时候,以常数项的因子来试根。用+-1,+-2,+-3,....+-28试。得到一个根后,再用常除法来除:
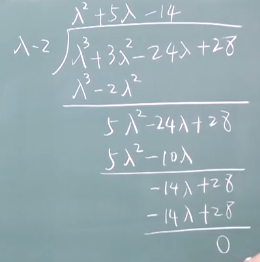


降秩的方阵0一定是他的特征值,而满秩的方阵或可逆的方阵,0一定不是他的特征值。


三、特征值与特征向量的性质








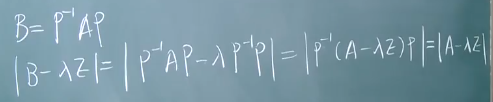

A*的特征值就是|A|除以A-1的特征值。
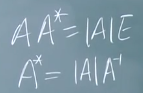
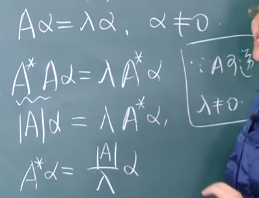

矩阵相似对角化的步骤:

一般矩阵对角化的问题,当他有重特征值的时候要判断一下它矩阵的秩,然后,当它与对角阵相似的时候,把它所有的特征值和特征向量求出来,所有特征向量组成了P,所有特征值组成Λ。