Finance_Analysis-of-Financial-Time-Series

金融时间序列分析讲义

 http://www.math.pku.edu.cn/teachers/lidf/course/fts/ftsnotes/html/_ftsnotes/rsoft.html

金融时间序列分析

https://blog.csdn.net/matrix_laboratory/article/details/53746745

方匡南

http://www.peixun.net/main.php?mod=search&ac=index&searchkey=%B7%BD%BF%EF%C4%CF

炼数成金

https://www.bilibili.com/video/av74184129?from=search&seid=11347244863603380021

检验中常见分布 https://www.cnblogs.com/tlfox2006/p/9989529.html

常见的时间序列的公式：

AR(1): y_t = β₀+β₁y_t-1+ξ_t

AR(q): y_t = β₀+β₁y_t-1+....+y_t-p+ξ_t

ARDL(p,q): y_t = β₀+β₁y_t-1+....+y_t-p+r₁x_t-1+...+r_qx_t-q+ξ_t 　　

ADL(1,1) ：y_t = β₀+β₁y_t-1+r₁x_t-1+ξ_t 

MA(1)：y_t = u+ξ_t+θξ_t-1

MA(q)：y_t = u+ξ_t+θ₁ξ_t-1+θ₂ξ_t-2+....+θ_qξ_t-q = u*Σθ_qξ_t-q

ARMA(p,q)：y_t = β₀+β₁y_t-1+....+y_t-p+ξ_t+θ₁ξ_t-1+θ₂ξ_t-2+....+θ_qξ_t-q

AR(1) -> MA(无穷)： y_t = β₀+β₁y_t-1+ξ_t -->  yt = β₀/1-β₁ + ξ_t+β₁ξ_t-1+β₂ξ_t-2+....+β_qξ_t-q 

2.1 线性时间序列分析即应用

 

 

 

 

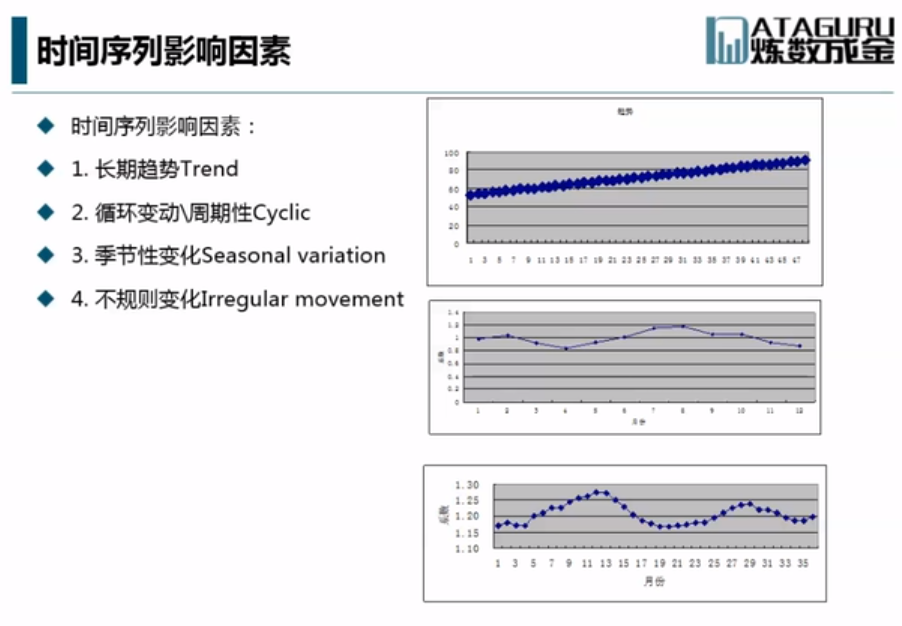
 一般都是用样本估计来

相关系数不会被单位变化而变化，用于比较。

2.2 随机游动

 

 

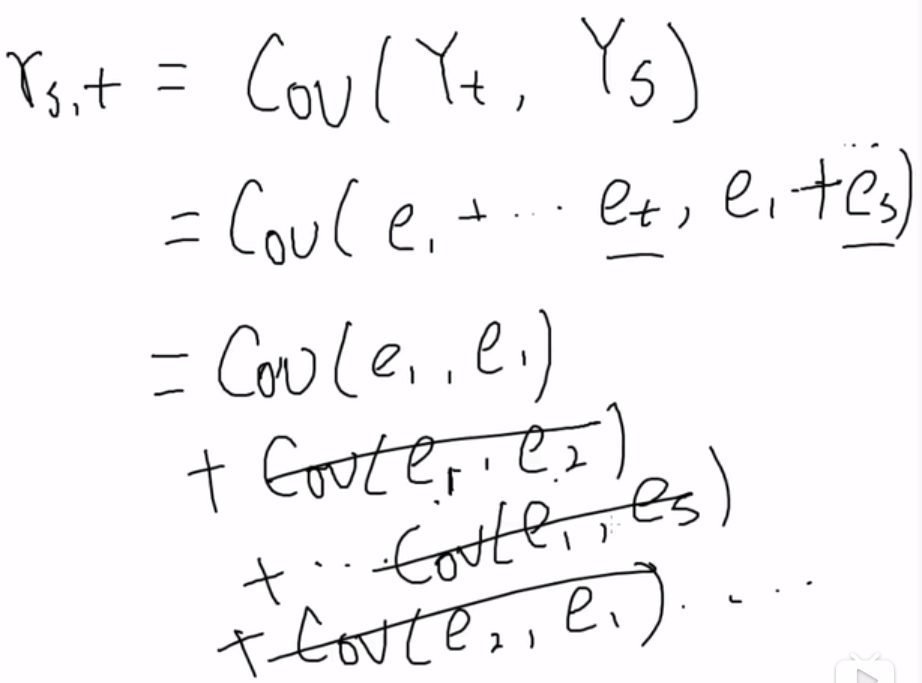
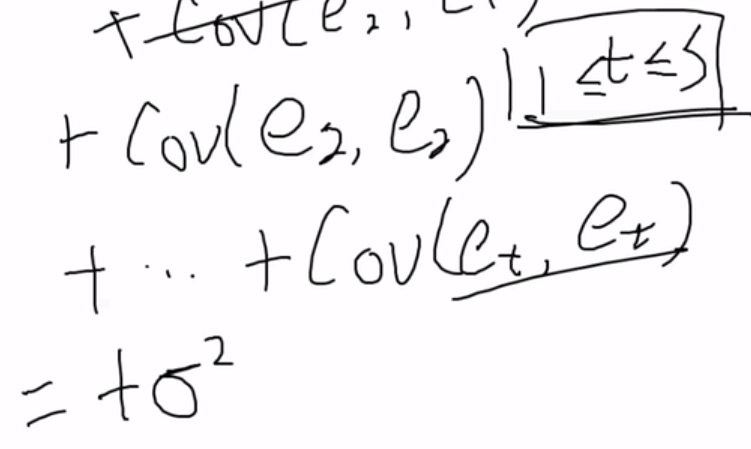
下标不一样的cov都是0，所以r=cov(ei, ei)= t*σ²。

 

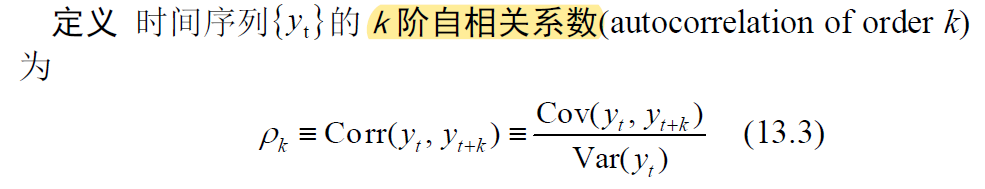
对于严格平稳过程， Pk不依赖于具体时间，仅是滞后阶数k 的函数，称为“自相关函数”(Autocorrelation Function，简记ACF)。

 

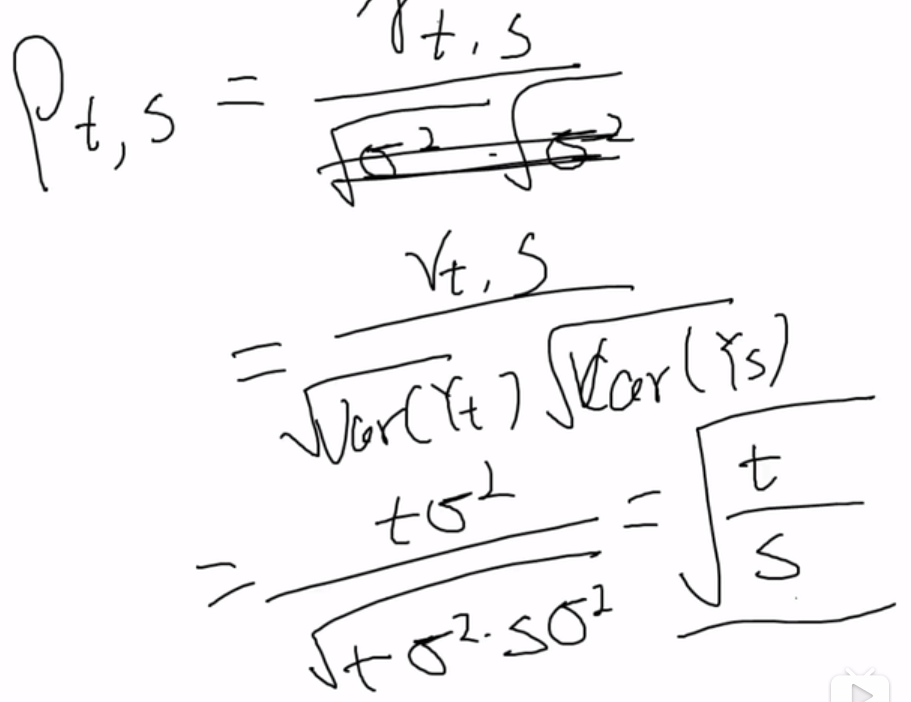
这说明，时间较近时，相关性越强，时间越远，相关性越弱。

 

严格平稳：同分布

弱平稳：2阶moment相同。

2.3 假设检验

相关性检验的方法：1. 检查单个ACF：T Rules 2. 混成检验：Q检验

t比是t检验。T分布：将卡方分布放在分子，并除以自由度，而将正态分布放在分母，就得到了t分布。

当Pi=0，T-ratio服从标准正态分布。假设H₀：Pl=0。当|t-ratio|>Z_a/2时拒绝H_0。

> da=read.table("m-decile1510.txt")
> head(da)
> dav4=da$V4
> dec10= ts(dav4,frequency = 12,start = c(1960,1))
> par(mfcol=c(2,1))
> plot(dec10,xlab='year',ylab='returns')
> title(main='(a): Simple returns')
> acf(dav4,lag=24)
> f1=acf(dav4,lag=24)
> fa$acf
> tt=f1$acf[13]=sqrt(516)
> tt

 

Box.test（Q检验）是用于检验是否是随机过程，他们数据之间是否存在相关性。p-value>5%，则ibm股票收益率前后具有相关性。

>da=read.table("m-ibmsp6709.txt")
> head(da)
> ibm=da$ibm
> lnibm=log(ibm+1)
> acf(ibm)                #用ACF检验
> Box.test(ibm,lag=12,type = "Ljung")         用Box检验

{et} 序列是具有有限方差和有限均值，独立同分布的随机变量的话，那么这样的序列叫做白噪声。

3.1 时间序列分析

AR(1): y_t = β₀+β₁y_t-1+ξ_t

AR(p): y_t = β₀+β₁y_t-1+....+y_t-p+ξ_t

ARDL(p,q): y_t = β₀+β₁y_t-1+....+y_t-p+r₁x_t-1+...+r_qx_t-q+ξ_t 　　

ADL(1,1) ：y_t = β₀+β₁y_t-1+r₁x_t-1+ξ_t 

MA(1)：y_t = u+ξ_t+θξ_t-1

MA(q)：y_t = u+ξ_t+θ₁ξ_t-1+θ₂ξ_t-2+....+θ_qξ_t-q = u*Σθ_qξ_t-q

ARMA(p,q)：y_t = β₀+β₁y_t-1+....+y_t-p+ξ_t+θ₁ξ_t-1+θ₂ξ_t-2+....+θ_qξ_t-q

AR(1) -> MA(无穷)： y_t = β₀+β₁y_t-1+ξ_t -->  yt = β₀/1-β₁ + ξ_t+β₁ξ_t-1+β₂ξ_t-2+....+β_qξ_t-q  

β = Φ  y_t=x_t  ξ_t=a_t

 

这里的线性时间序列是指MA(无穷)：yt = a+Σθ*ξ_t。Theta要求<1，这样MA(无穷)就不是随机游走。且Et随着时间间隔增大，对yt的影响也会越来越小。

经济意义：收益率是会受前期扰动的影响，但前期的随机扰动的影响会越来越小。且收益率之间的相关性，也会随着时间间隔增加而增加。

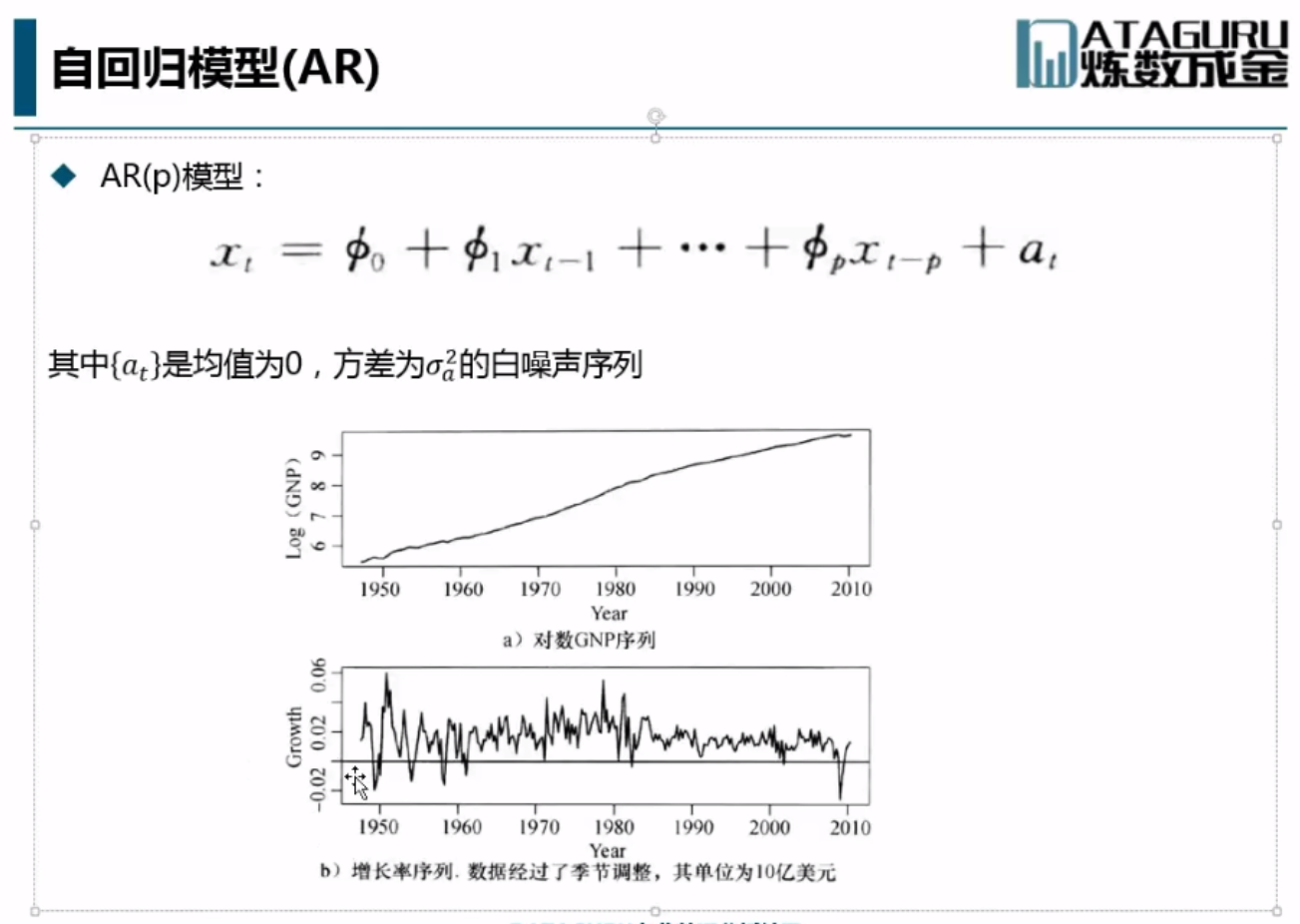
AR(p)模型：yt=β₀+β₁*yt-1+...+β_p*yt-p+Et。

经济含义：当前t期的收益率是与t-p时刻的收益率是有关系的。与前期的扰动项无关，只与当期扰动项相关，即前定

 

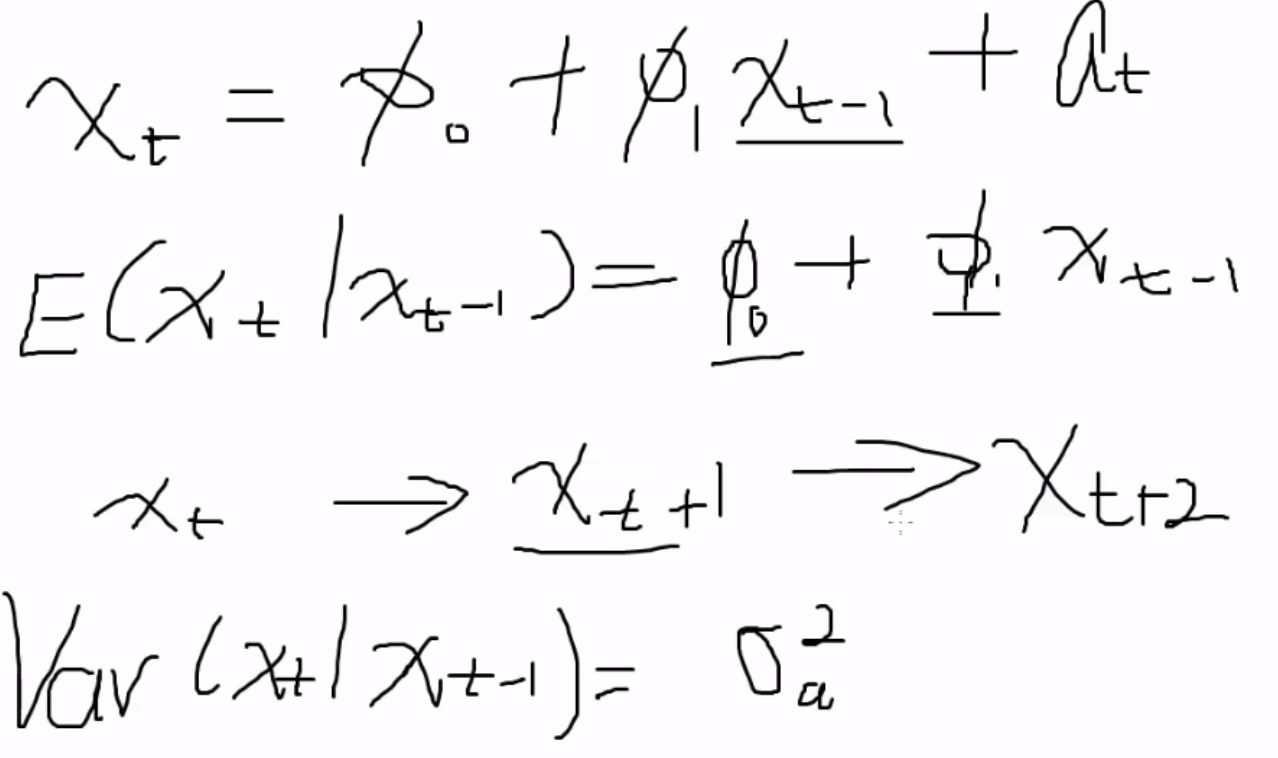
AR(1)模型：我们可以通过t-1时刻的数据去预测t时刻的收益率。

  

E(xt)=E(xt-1)=μ 且 Φ₁不等于1。（β=Φ，ξ_t=a_t）

AR(1) -> MA(无穷) 

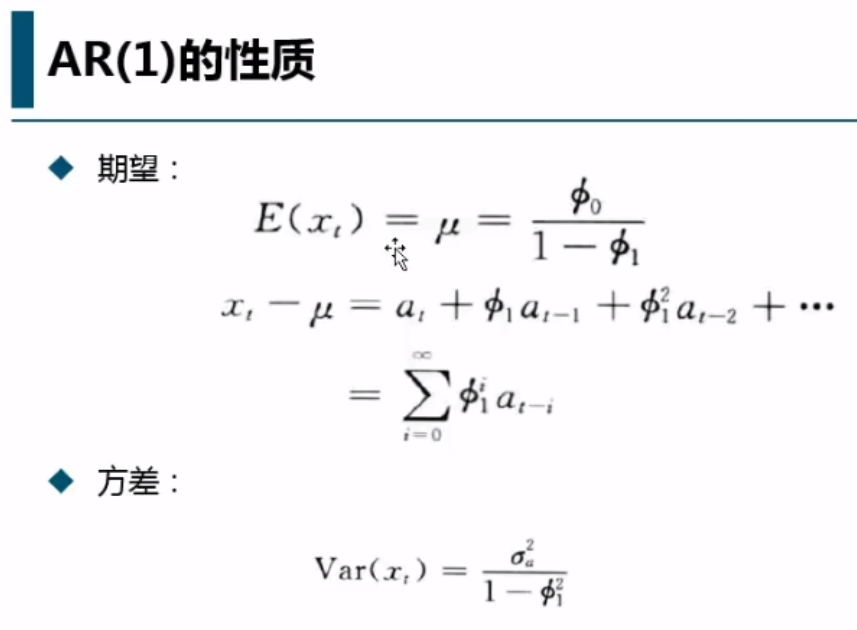
Var(xt)=Var(xt-1) -> Var(x)= σ²/1-Φ₁²

AR(1): Var(yt)=0+β₁²*Var(yt-1) + σ² ---(Var(yt)=Var(yt-1)---> Var(yt)= σ²/1-β₁²

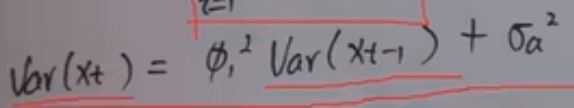
 Φ₁²不等于0. 如果{xt}是弱平稳的话，则Φ₁<1。

 AR(1)自相关性

等式两边同乘以at，后再取期望：

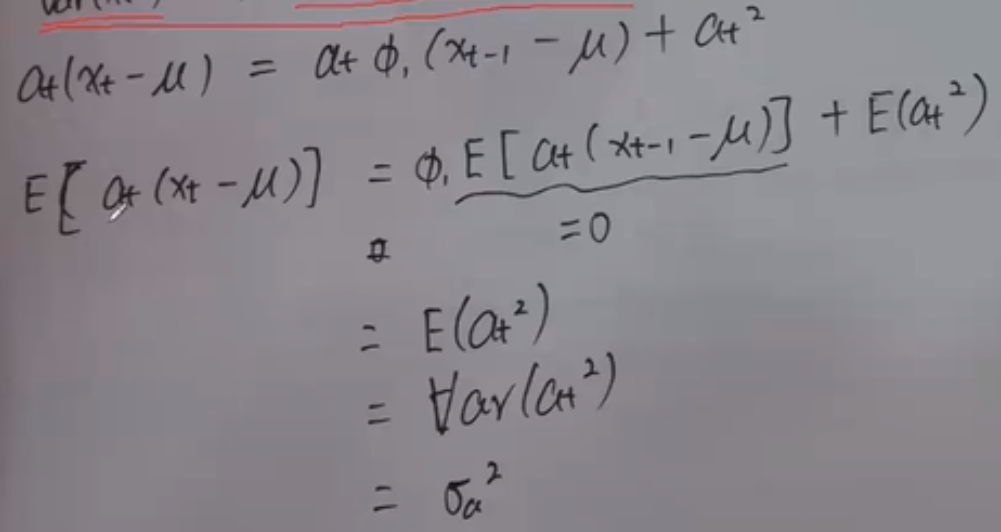
P_l= Φ₁*P_l-1 --> P_l=Φ₁^j

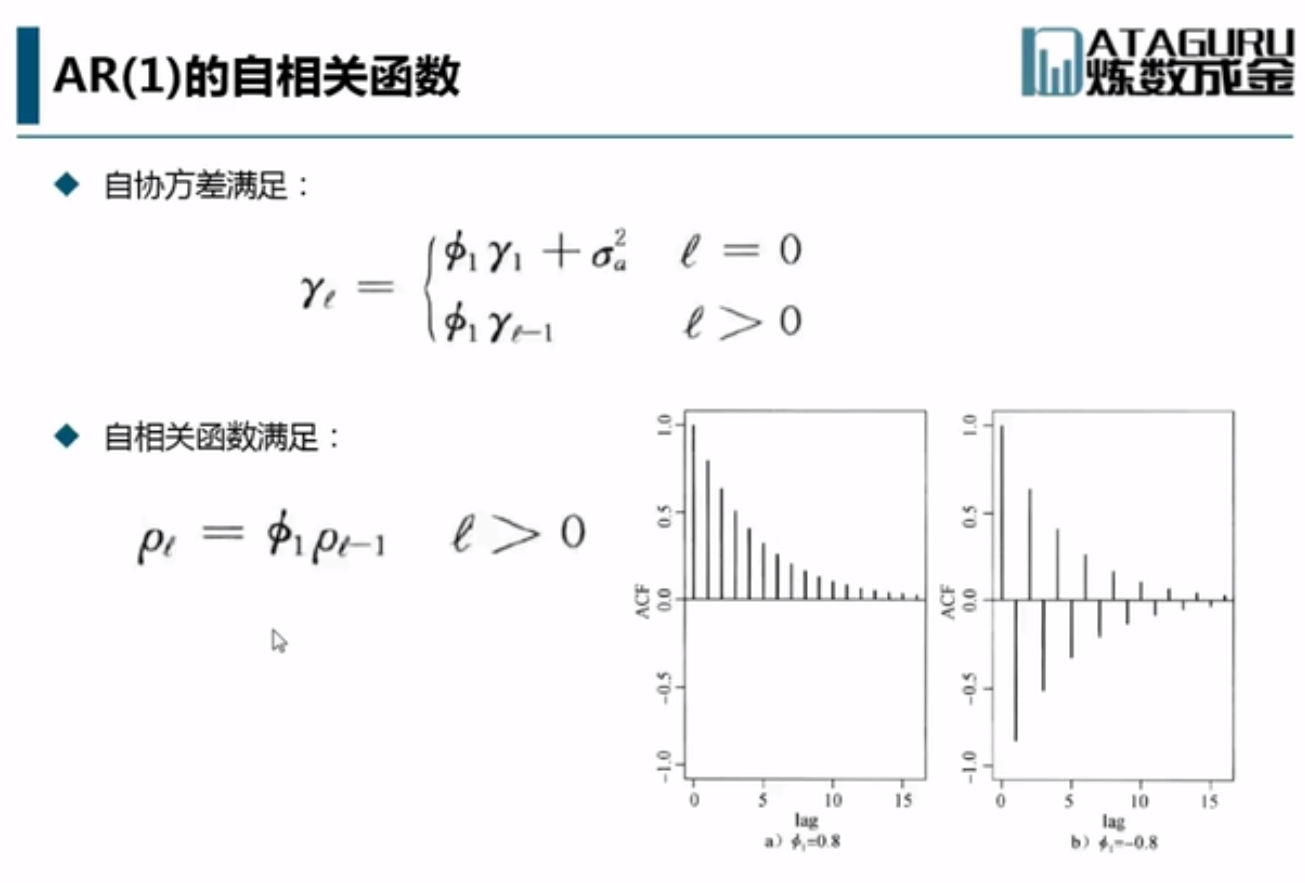
3.2 AR(2)& AR(p)

y_t-p = B (滞后算子) β=Φ

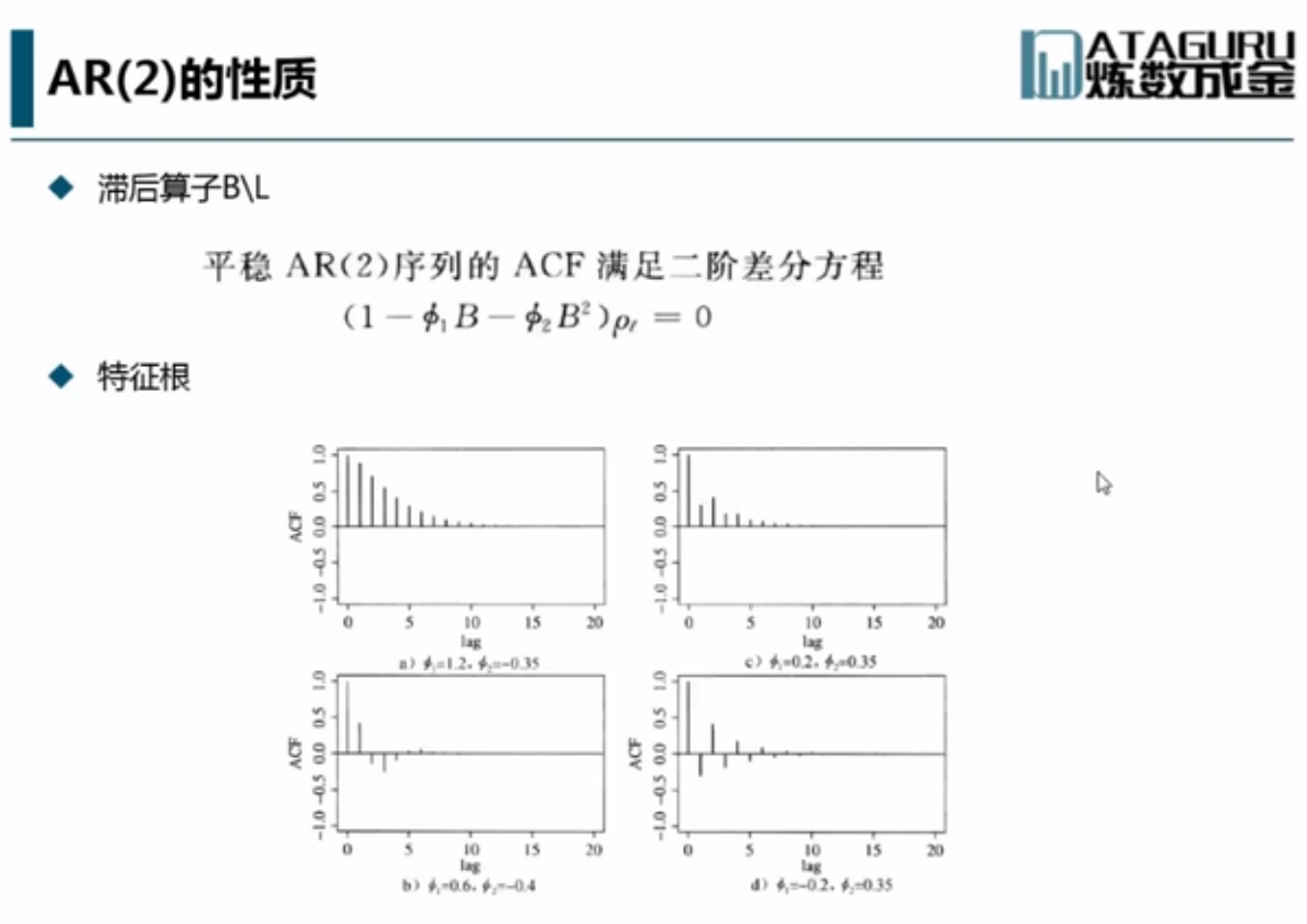
上图的根为实数根，而下两图的根为复数根，所以他们显示周期变化。特征根的模要小于1。

E(xt)=E(xt-1) = μ

yt-p = B (滞后算子)  B*P_l =P_l-1 <- Bⁿ*P_l = P_l-n = Z 

 

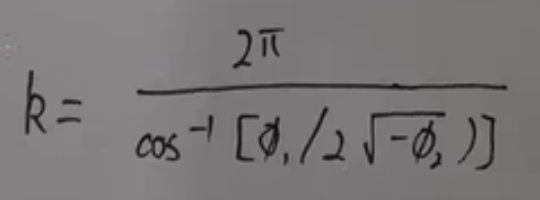
AR(2)的齐次方程：Φ(z) = 1-β₁z-β2Z²=0。特征根ω1=1/z1；ω2=1/z2。当特征根的绝对值|1/z_j|<1的时候，{yt}序列才是一个平稳序列。一元二次方程，在实数平面上比一定有解，但在复数平面上一定有2个解。

k为随机的平均周期。 

AR(p)的齐次方程：Φ(z) = 1-β₁z-...-β_pZ^p=0。 有p个有实数和复数根。特征根的形式为1/z_i。

  

AR(p)确定P的阶数

AR(p): y_t = β₀+β₁y_t-1+....+y_t-p+ξ_t

方法1： T rules

考虑这些列的AR模型，考虑AR模型的话，P阶的ACF的自相关系数是不为0的，而大于P阶的话，是非常接近于0的。所以可以看PACF在哪等于0，来确定P的阶数。

 方法2：BIC和AIC：找到P使得BIC和AIC最小。

 

 

 

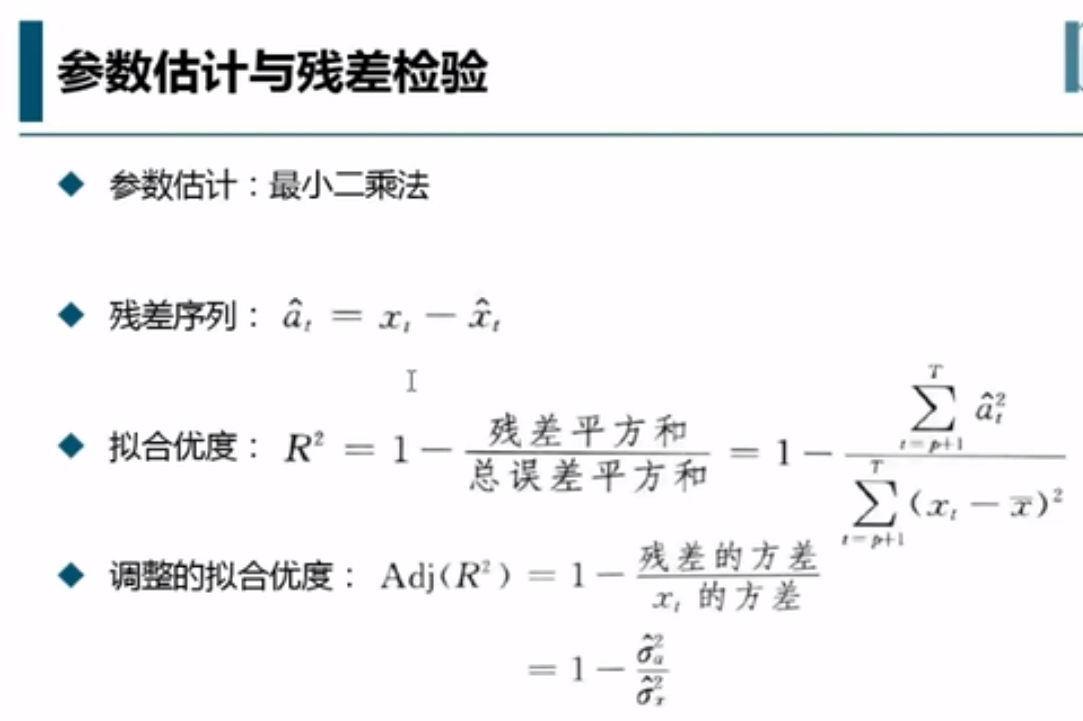
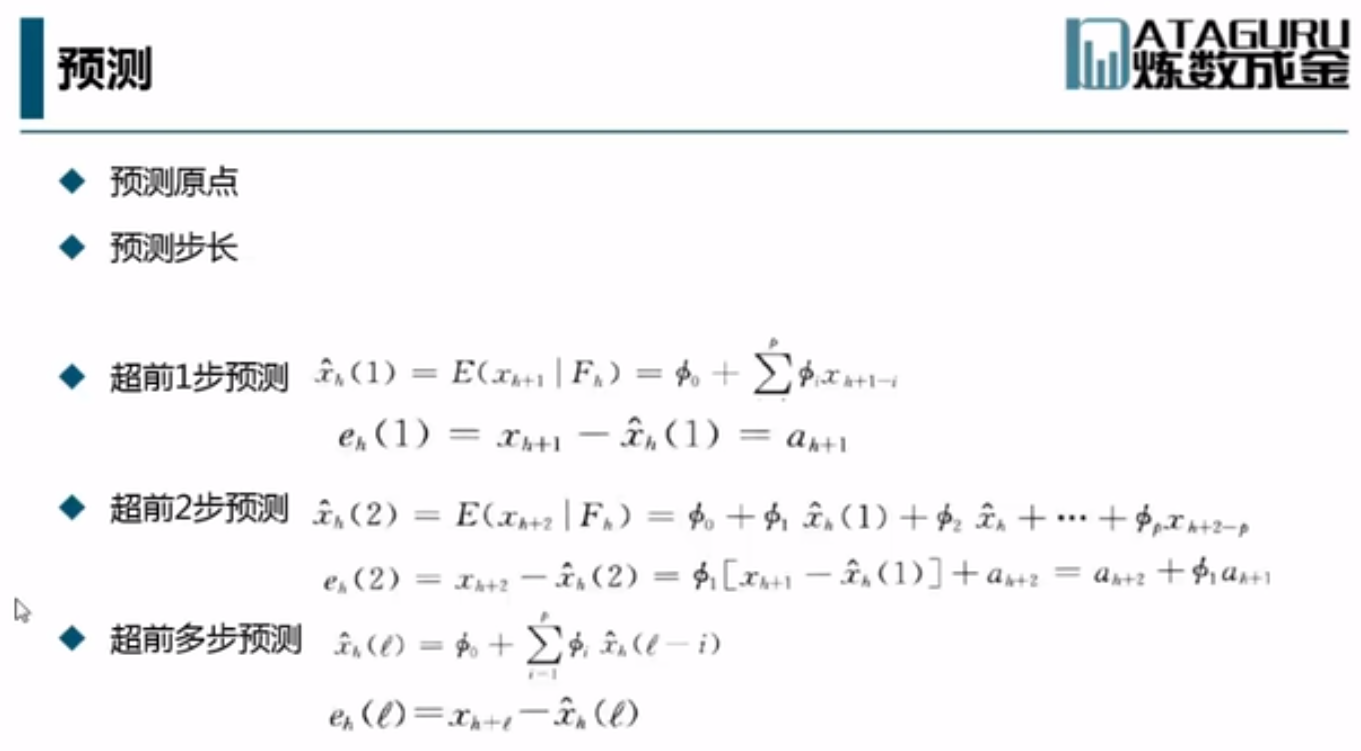
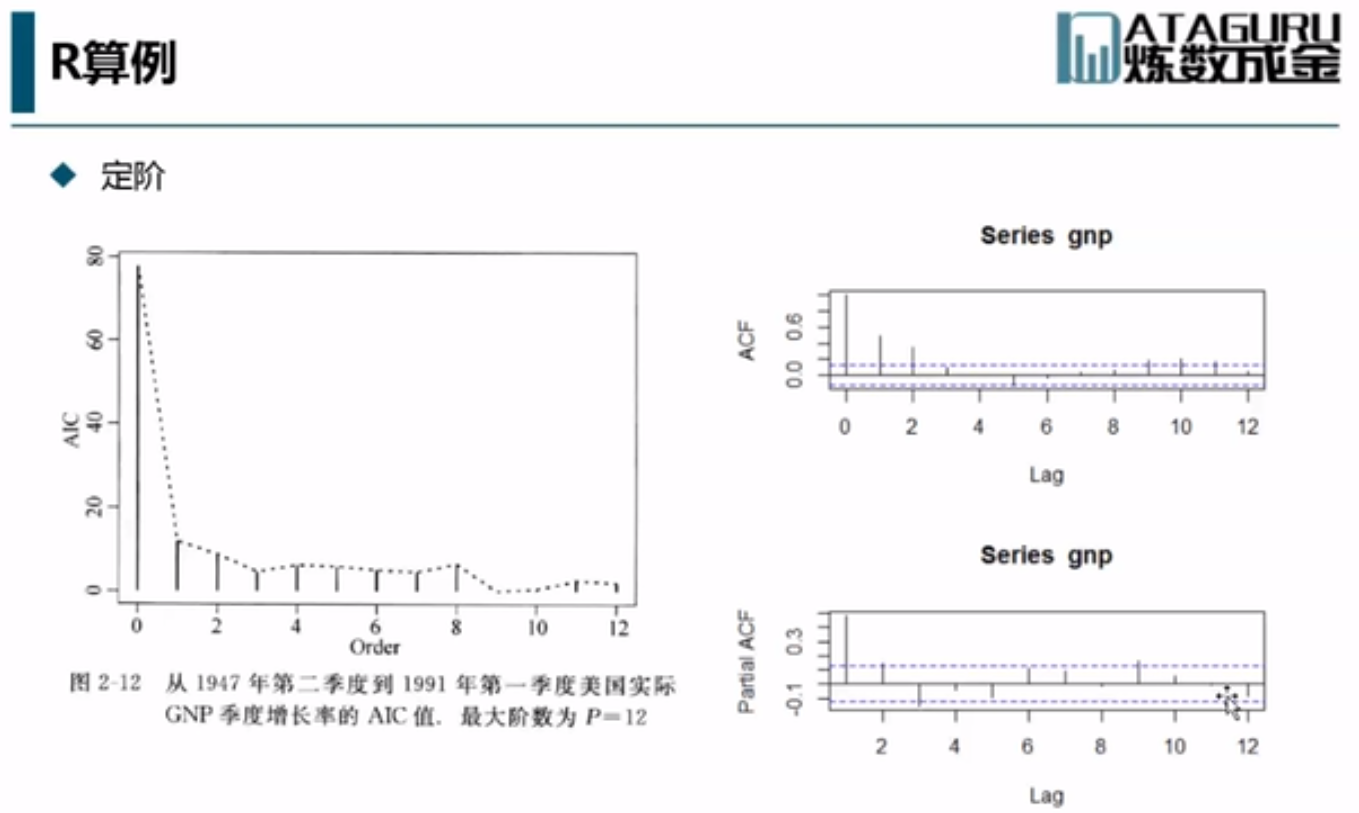
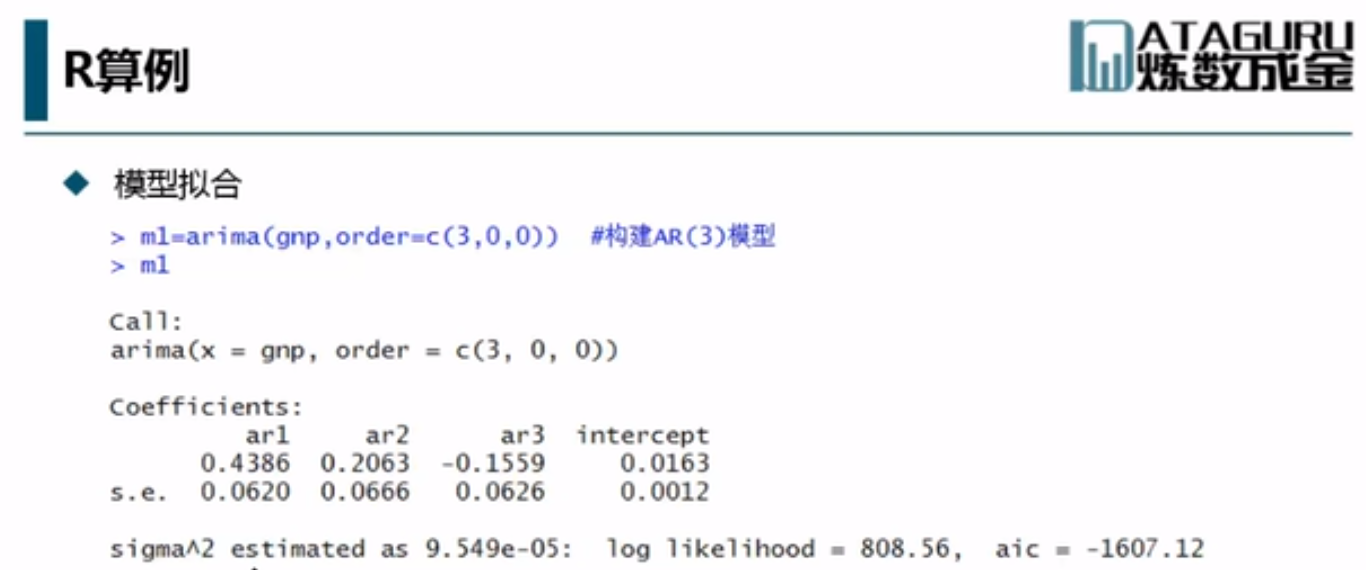
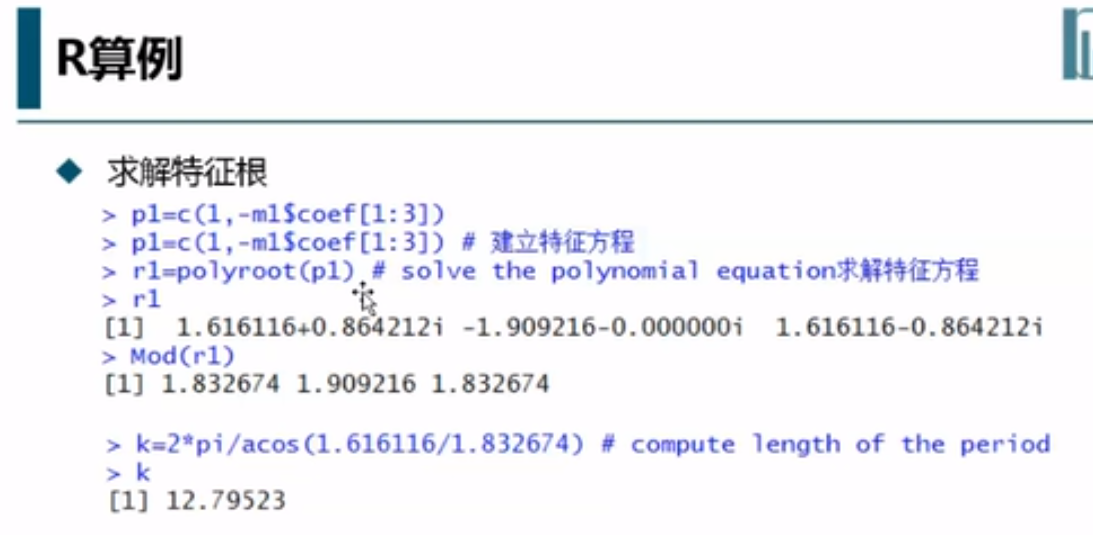
特征根都是大于1的，所以它是平稳序列。 k是周期，每12个月算一个周期。

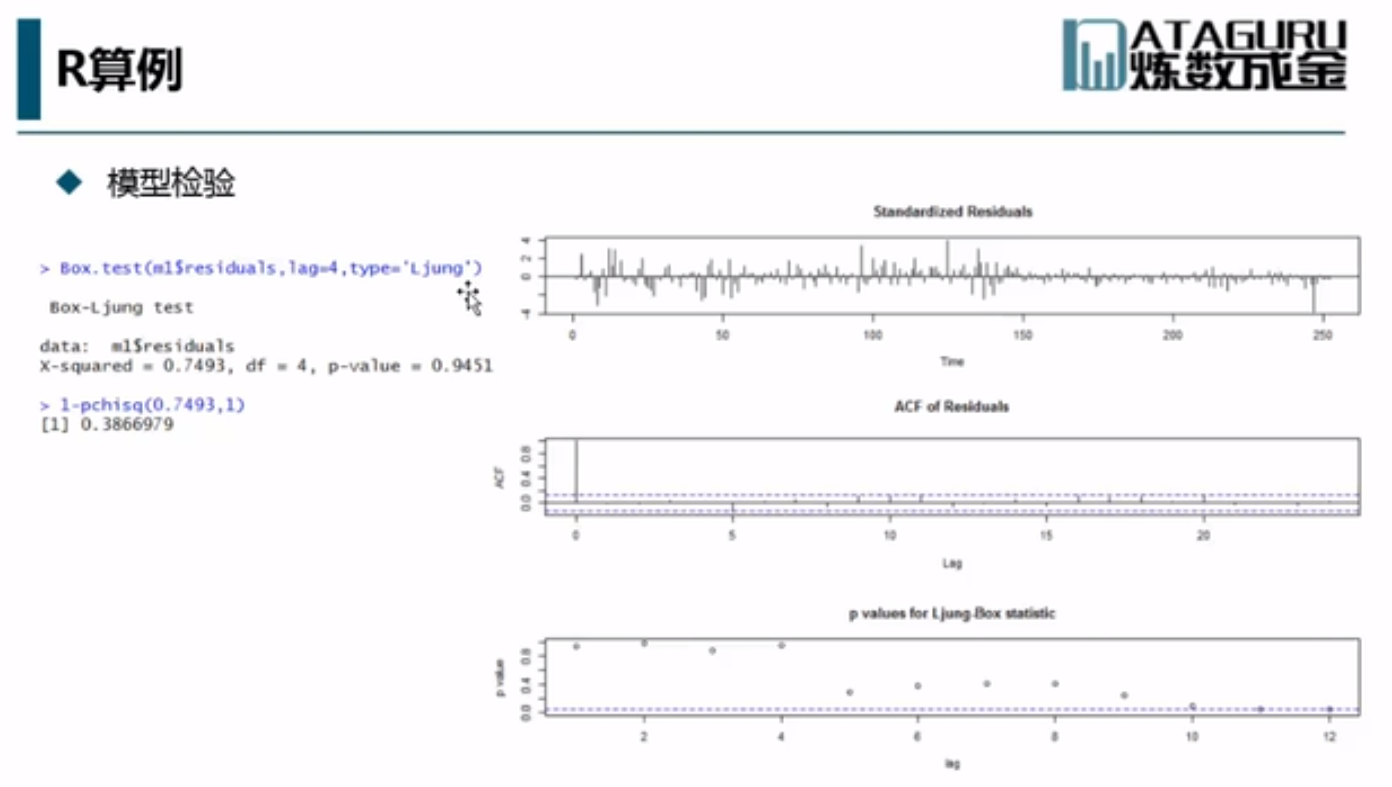
3.3 MA

MA(q): yt=u+ξ_t+θ₁ξ_t-1+θ₂ξ_t-2+θ₃ξ_t-3+...+θ_qξ_t-q = u + Σξ_t-q  --> x_t=c₀+a_t+θ₁a_t-1+θ₂a_t-2+θ₃a_t-3+...+θ_qa_t-q

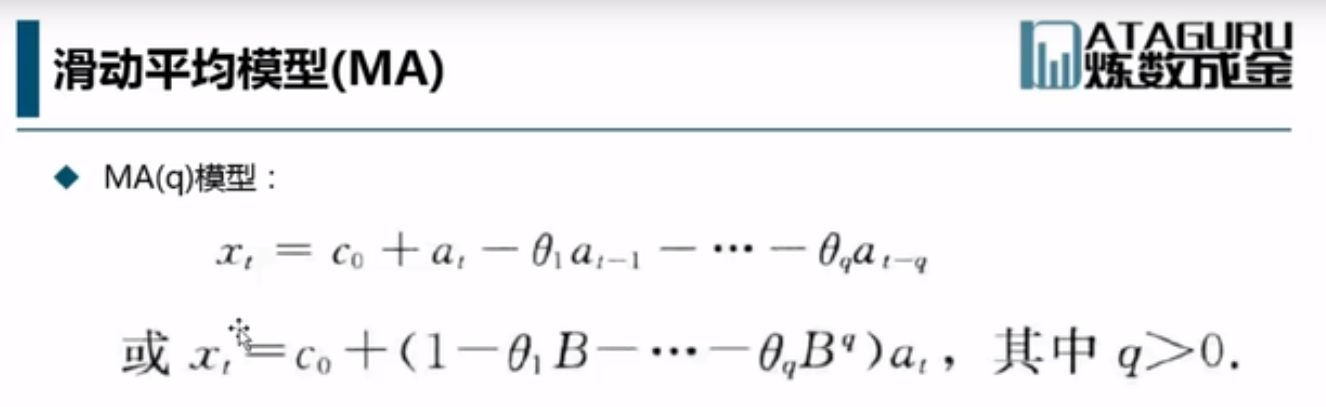
 MA(q)是与上一期及上几期的随机扰动有关，而与收益率无关。这就与AR(p)模型不同，AR(p)只与过去的收益率和本期扰动项有关。

B是滞后算子，是个函数而不是简单的数字。MA模型也可以写成B的公式。

MA(1): x_t=c₀+a_t+θa_t-1

 

 定阶方法：1.看ACF图，看超过方差的部分。2. 利用BIC和AIC来定阶。

 

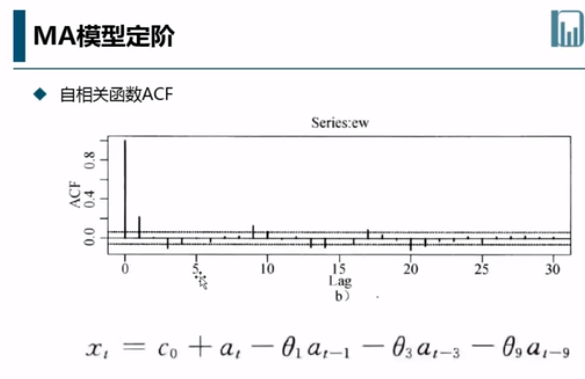
一般建立模型不会取太高的阶数，只有在简单的模型无法适用的时候，才会考虑高阶模型。

MA(q)做回归，不能用OLS做回归，只能用MLE（最大似然法）.

 

条件似然法：假设初始扰动都为0. 这样由a1=x₁-c₀得到a1，a₂=x₂-c0+θ*a1 得到a2...， 可推得到计算似然函数所需要的“扰动”。

精确似然法：当模型得附加参数与其他参数一期估计出来。

精确似然法计算得精度更高，但代价也更大。当样本量不太大得时候， 我们采用精确似然法。

MA(1)模型得向前一步得预测即达到序列得均值。 而MA(2)模型得向前两步得预测即达到序列的均值。这样，MA(q)模型，向前q步得预测即达到序列的均值。对于MA(9)，第10步就可以得到均值。

3.4 ARMA

ARMA(p,q)：y_t = β₀+β₁y_t-1+....+y_t-p+ξ_t+θ₁ξ_t-1+θ₂ξ_t-2+....+θ_qξ_t-q

ARMA(1,1)：ARMA(p,q)：y_t = β₀+β₁y_t-1+θ₁ξ_t-1

 

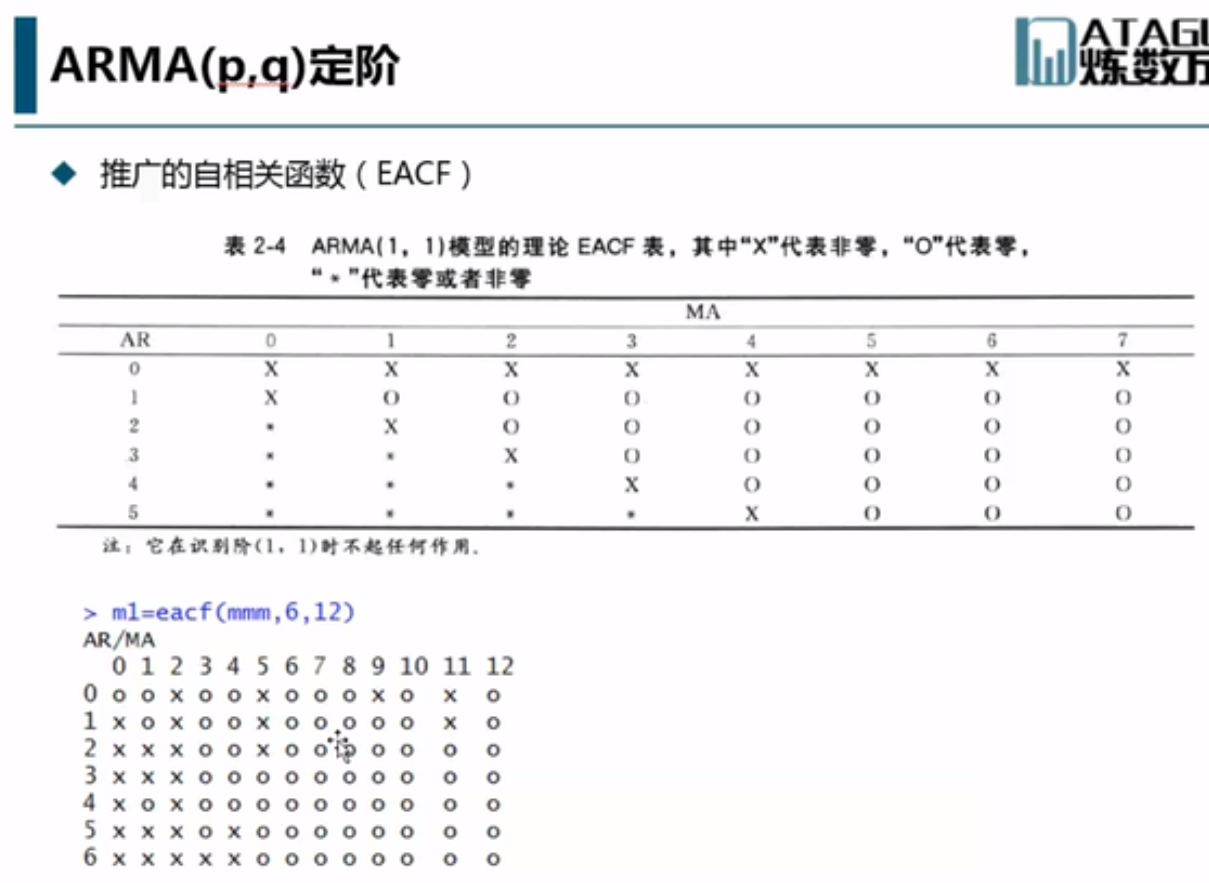
ARMA使用EACF来定阶。一般用“o”所组成的三角形，并且这个三角形左上角顶点位于阶（1，1）处。这样来确定ARMA的阶。 

 如果o处于（0，0）处的话，说明它实际上是一个白噪声过程，就不适合做分析了。

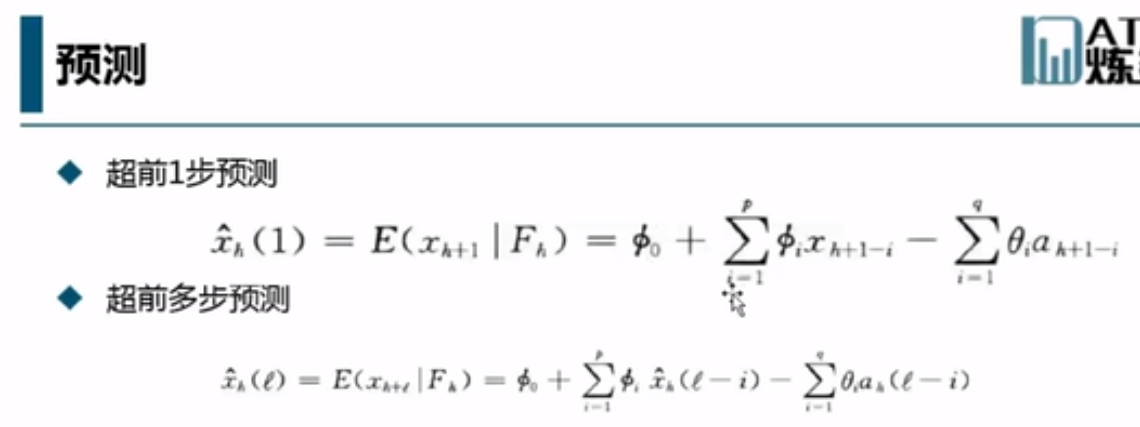
 ARMA是有三种表示方法。在不同场合下适用不同的表示方法。 

4.1 

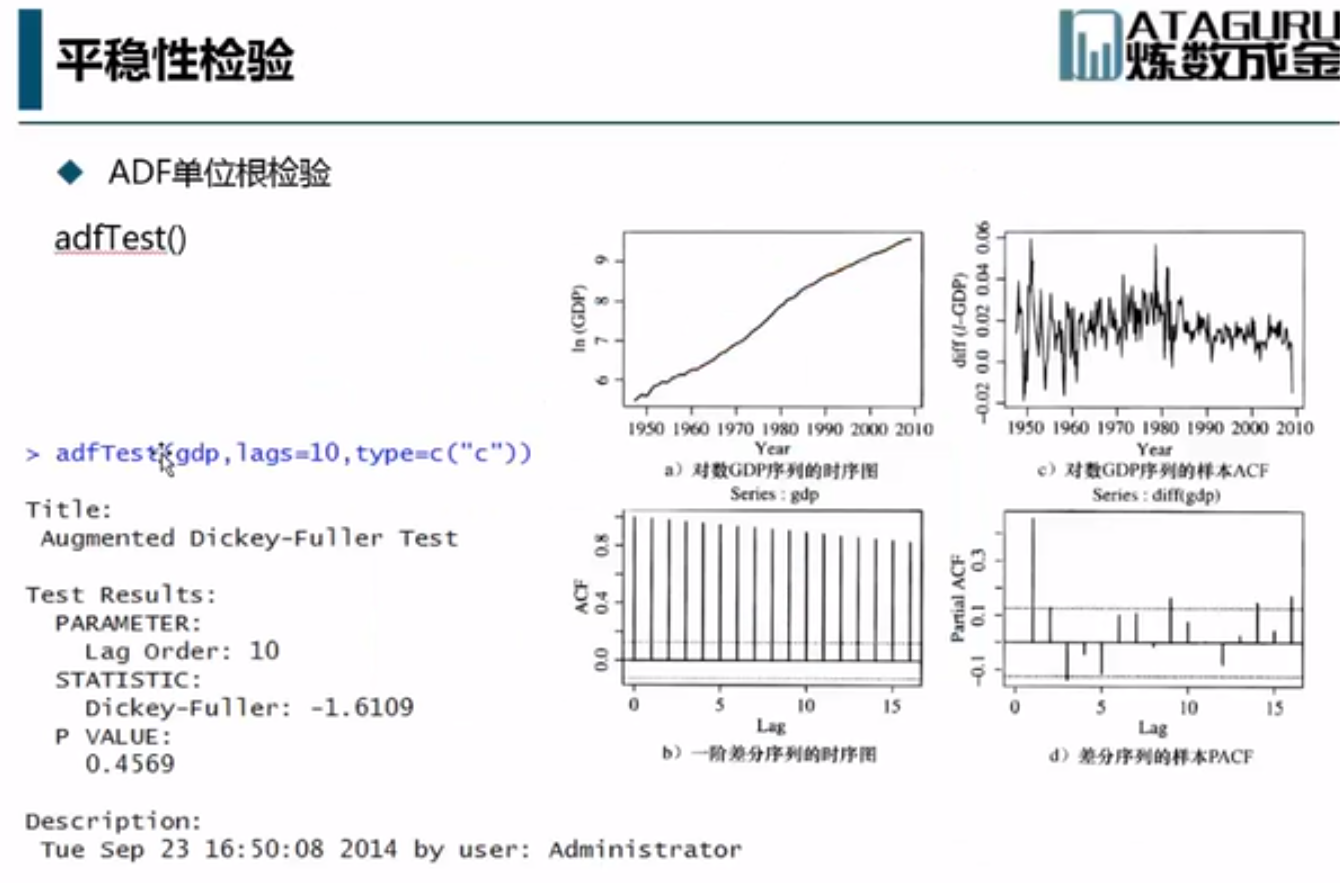
ADF检验，判断时间序列是否是平稳的时间序列。