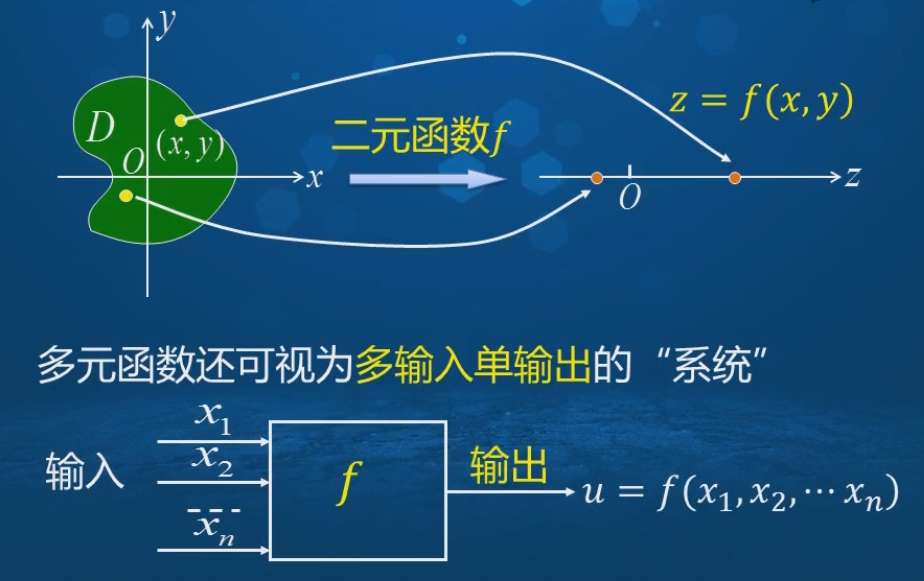
多元函数
1. 多元函数的定义:https://www.youtube.com/watch?v=jQygXb1BUaI
多元函数的特点:一个变量存在与其它多个变量的依赖关系。这种依赖关系我们成为多元函数。

n元函数:就是n元上的点集到实数集R之间的映射。无论是什么函数我们都是从一个集合到另一个集合之间的映射。

多元函数可以理解为是一个多输入,单输出的系统。

2. 多元函数的连续性 https://www.youtube.com/watch?v=mwpCHOqflGo

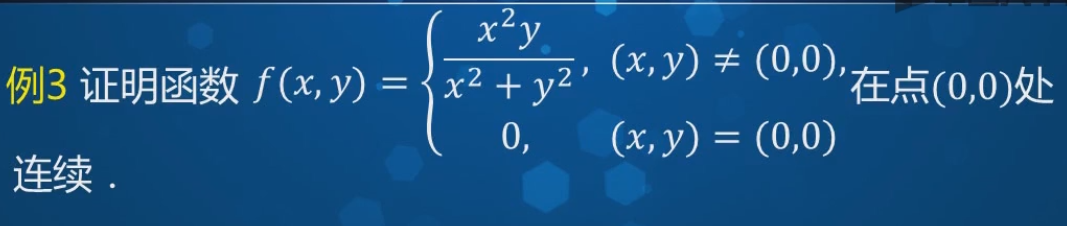
要证明这个函数在原点是连续的,就是要证明函数在原点的极限是等于0的。|f(x,y)| = |x2/x2+y2 * y| (其中x2/x2+y2 <=1),所以函数f(x,y)<=|y|.
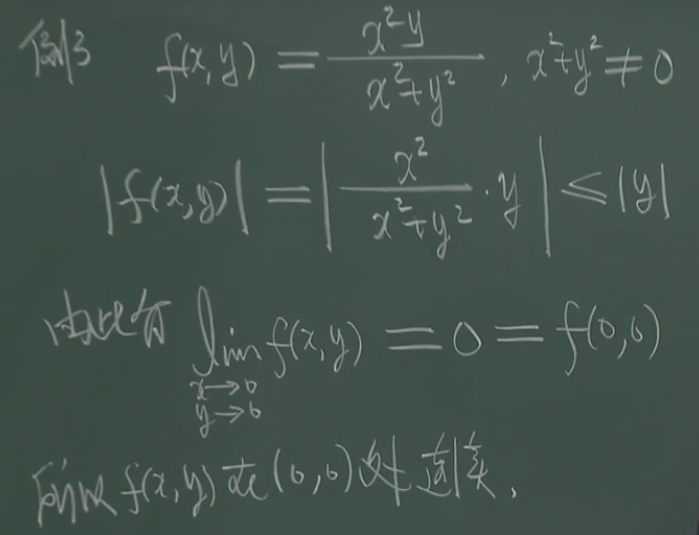
3. 函数可微必要与充分条件
全微分公式,可微,则函数一定连续。

偏导数存在,并不一定保证函数是连续的,但函数是可微的话,函数一定是连续的。
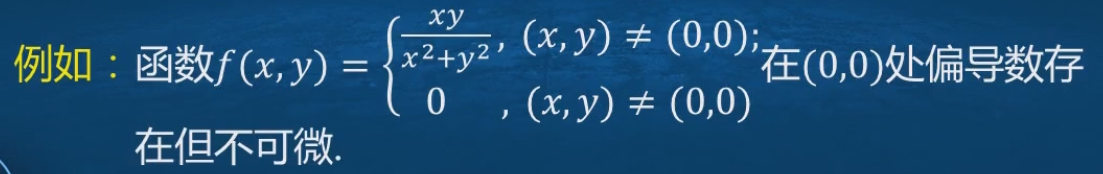
全微分的几何意义
曲面S:z=f(x,y) 函数是可微。在平面上的点分别对x,y做增量Δx,Δy,这样就从x0,y0变化到(x0+Δx,y0+Δy)。函数的增量的几何意义:指的是函数值从x0,y0这一点变化到(x0+Δx,y0+Δy)这点,所对应的函数值的增量。相应的全微分:是切平面方程(z=f(x0,y0)+f'x(x0,y0)(x-x0)+f'y(x0,y0)(y-y0).)所对应的函数从x0,y0,变化到(x0+Δx,y0+Δy)这点,所对应的函数值的增量。
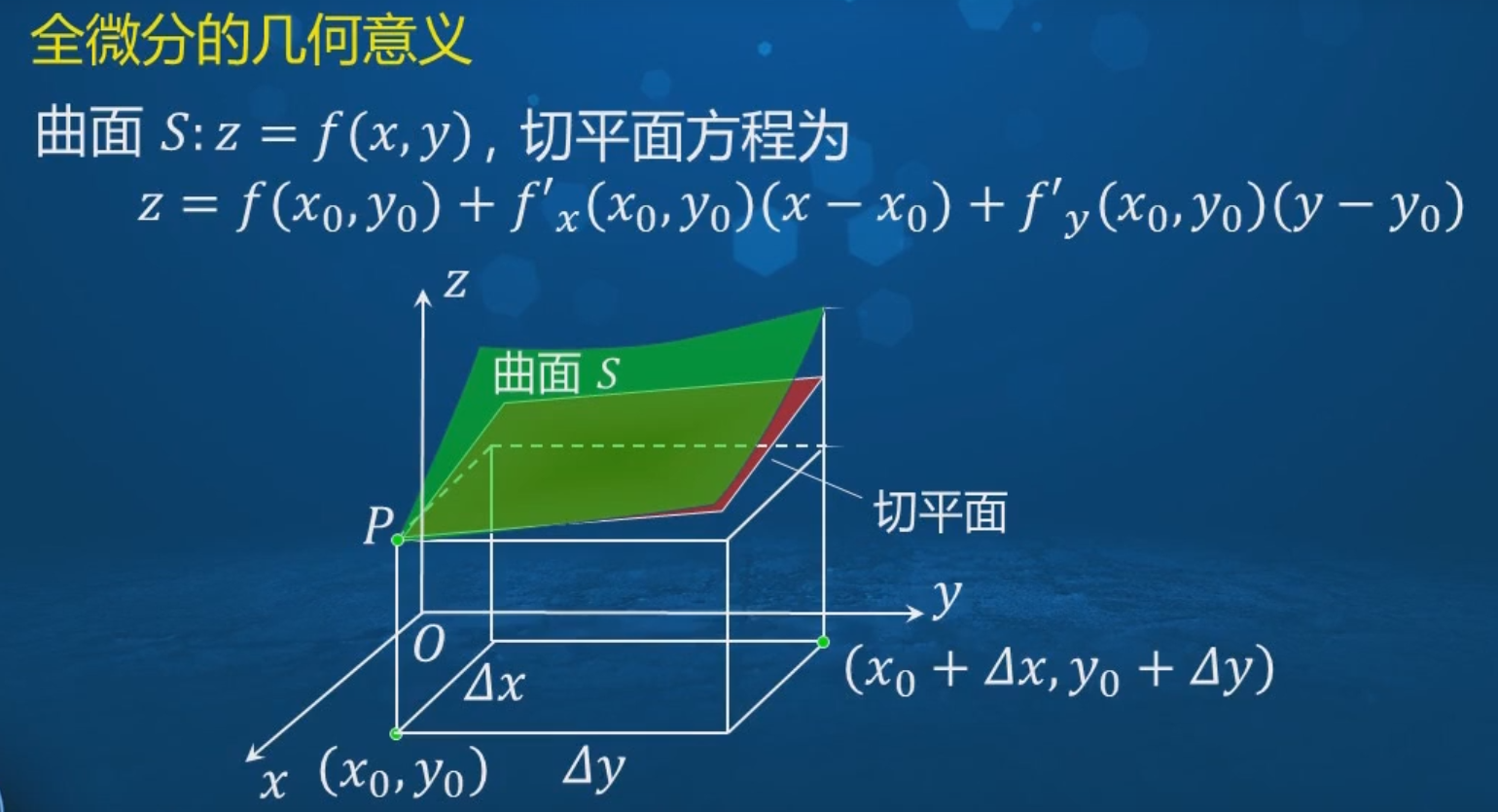
证明:
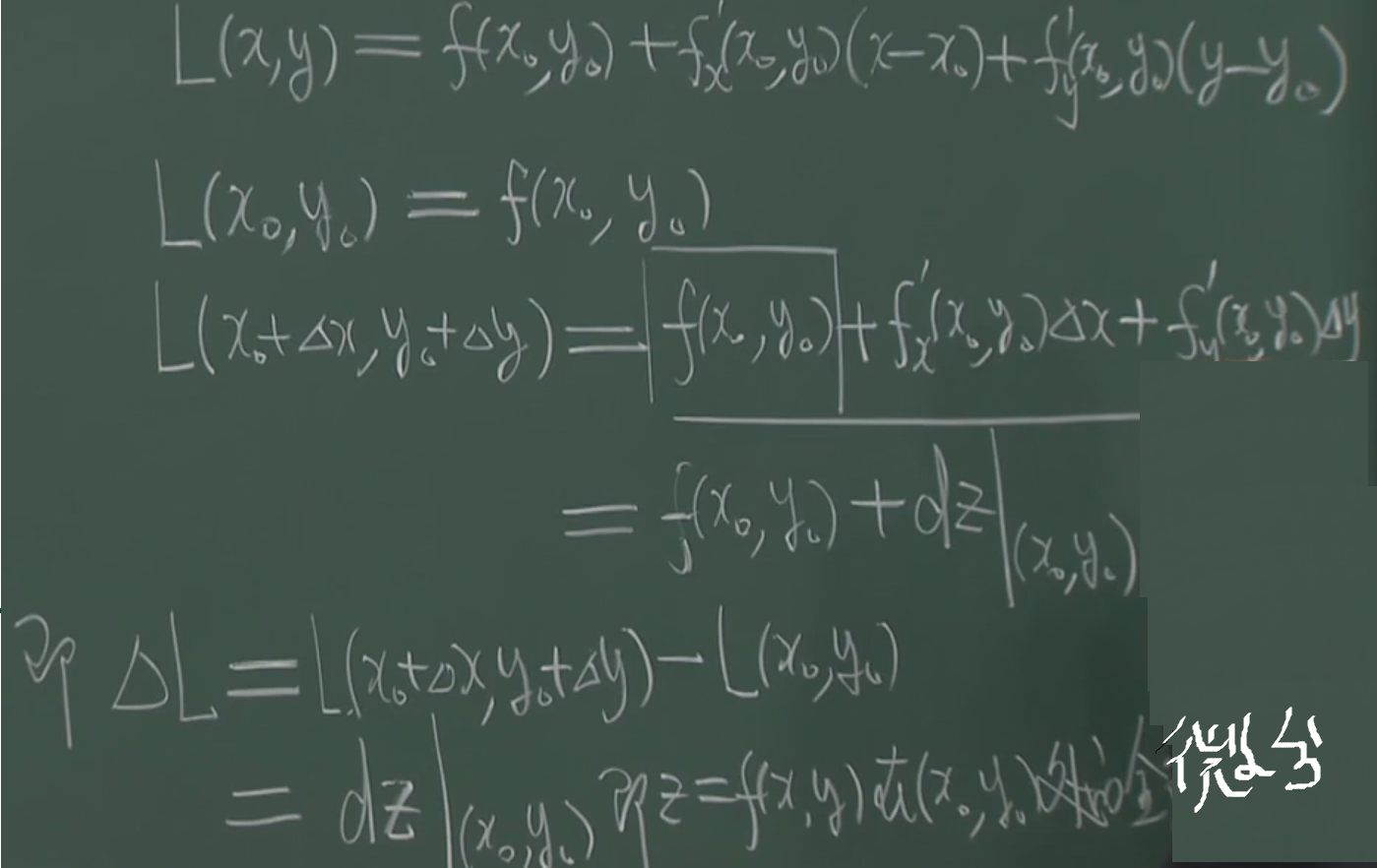
ΔL:切平面函数所对应的增量,即Z=f(x,y)函数在(x0,y0)的全微分。
因此,我们得到全微分的几何解释:切平面所对应的方程的函数从x0,y0变化到(x0+Δx,y0+Δy)的一个增量
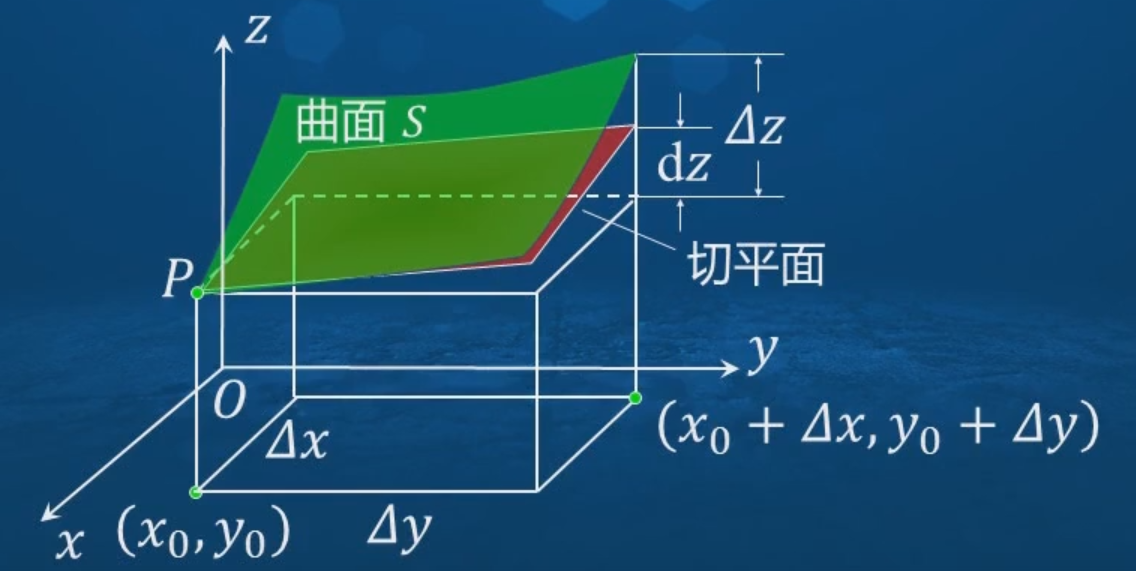
上图可以看见,ΔZ是函数的增量,而dZ是切平面的增量,即全微分。
全微分的几何意义:切平面上对应竖坐标的增量。
4. 梯度机器集合意义 https://www.youtube.com/watch?v=BDyX5C4etrU
向量相加,利用三角原理是叠加;向量点乘是投影。
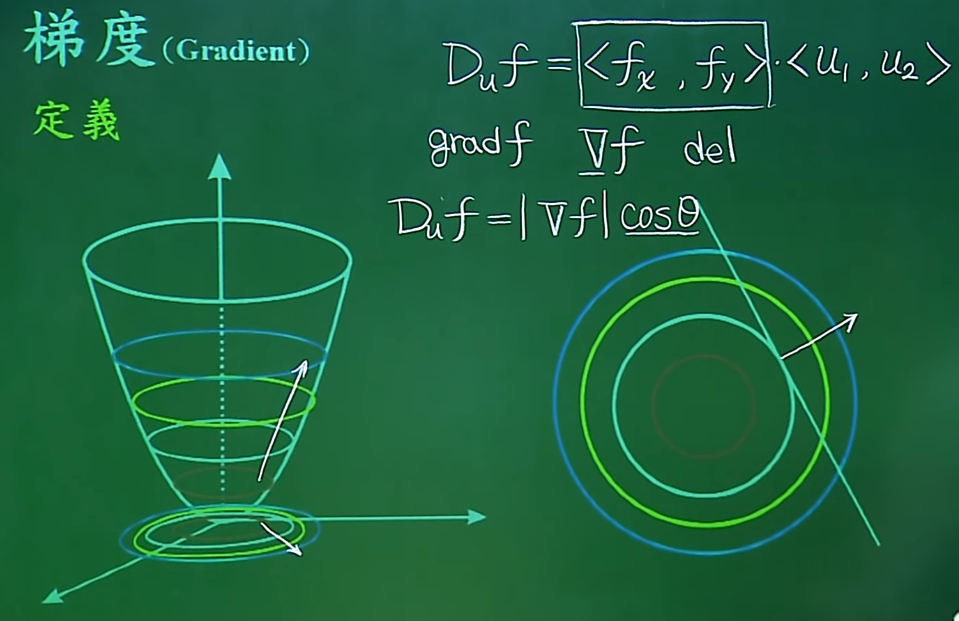
多元函数的方向导数:就是点在曲面上切线的斜率。对于2元函数f(x,y),在x,y关于u方向的方向导数:Duf(x,y) = df/dx*cosa + df/dy*cosβ。a,β分别为斜率与u向量方向的夹角。
方向导数也可以看成是两个向量的点乘。(cosa,cosb)正好是方向u的单位向量。梯度就是多元函数的切线斜率对方向向量的投影,我们把这样的向量称为梯度向量,简称梯度。

当cosθ=1的时候,即当νF与u的方向一致的时候,梯度是下降最快。u0是单位向量。

梯度就是沿曲面方向的切线;而方向导数是梯度在u方向的投影,梯度方向是与在等高线上的切线垂直。
综上,一个函数的梯度向量是与函数的变化是密切相关的。
方向导数表示成:梯度向量与方向的单位向量做点乘的结果。

所以,在计算2元函数和3元函数的方向导数的时候,要把梯度向量算出来,把方向向量单位化。然后把这两个向量做点乘,得到所需的方程组。
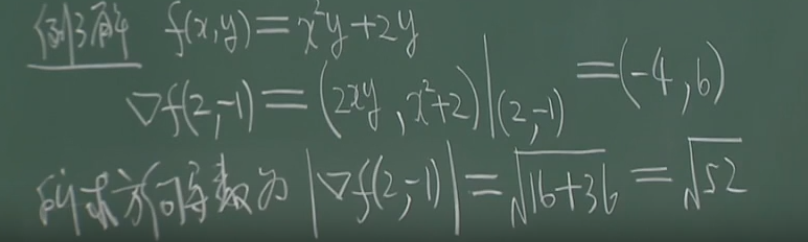
梯度的几何意义: https://www.youtube.com/watch?v=3-j85PUFM6Y
梯度的几何意义:梯度向量是与切向量垂直的。它的方向是保证函数值增加的方向。
二维函数f(x,y),其切向量为T (1, dy/dx) = (1, f'x/f'y) (隐含函数)。取与T平行的向量(f'y, -f'x)
梯度向量:νF=(f'x,f'y),梯度向量和切向量互相垂直。

5. 极大值极小值

海塞矩阵是f对于各变量的二阶偏导数,如果各二阶偏导数都是连续的话,这个矩阵就是一个是对称矩阵(正定/负定)。多元函数的二阶导数是正还是负,则是判断海塞矩阵是正定还是负定。


公式简化后:
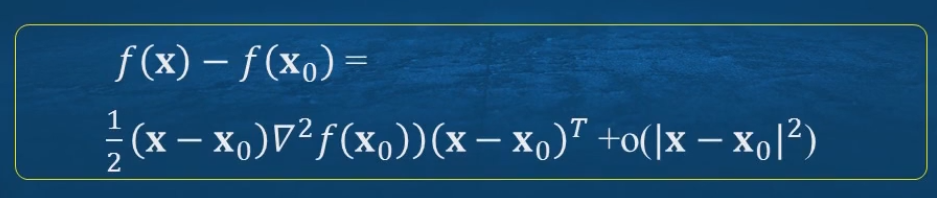

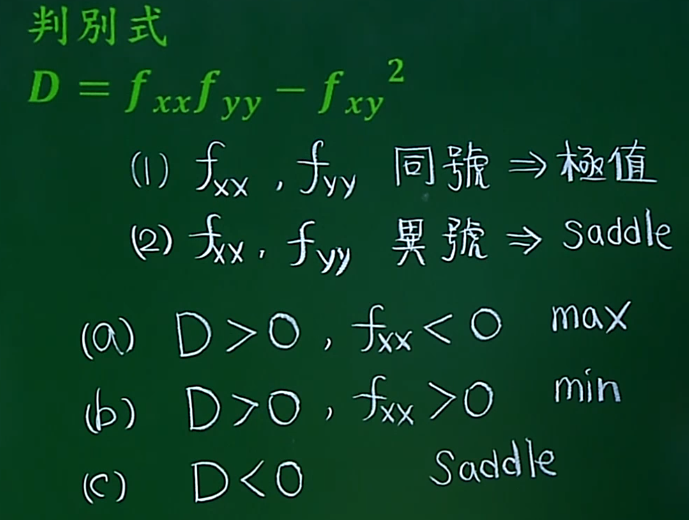
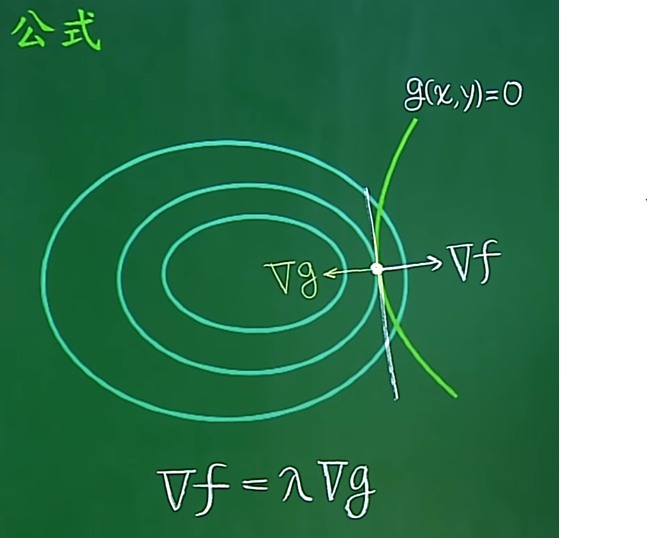
6. 拉格朗日乘子法: https://www.youtube.com/watch?v=nOcvxjB6YgA
http://aca.cust.edu.tw/online/custcourses/index.html#
1. 三维空间坐标几何
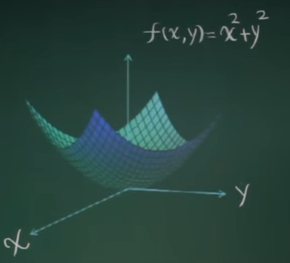
单变量函数:平面曲线。
双变量函数:空间曲面
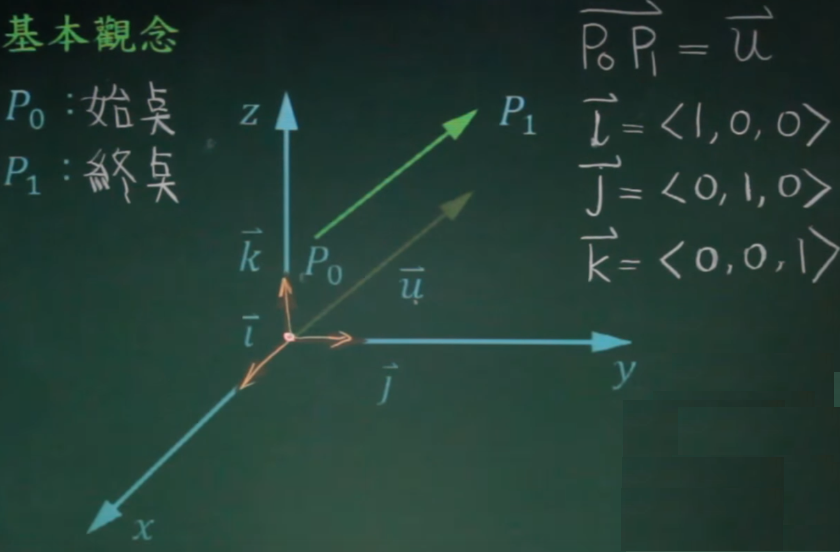
2. 三度空间的向量
单位向量:i向量,j向量,k向量,向量模长为1。i,j,k为基底。

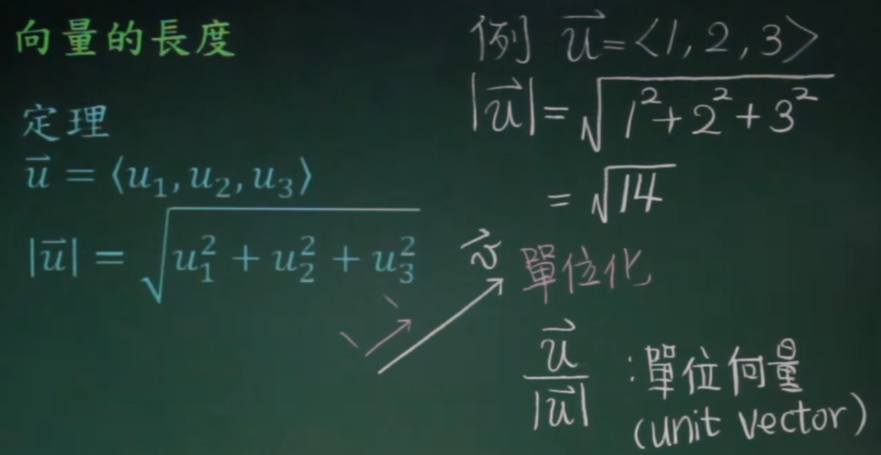
向量的运算
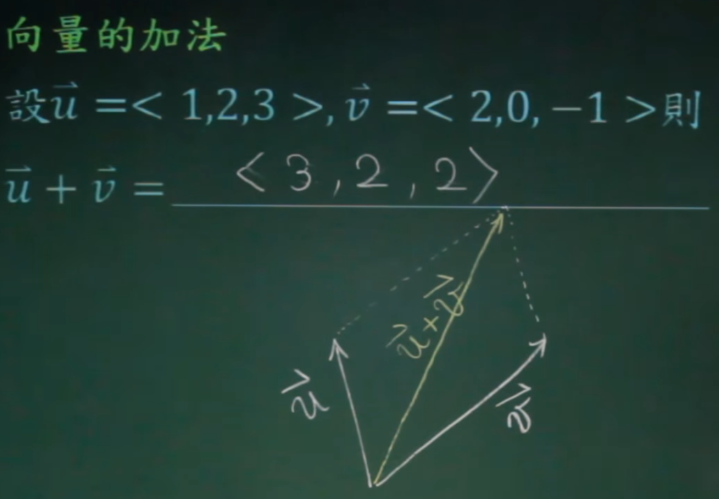
三角形不等式:|u向量+v向量| <= | u向量|+|v向量|

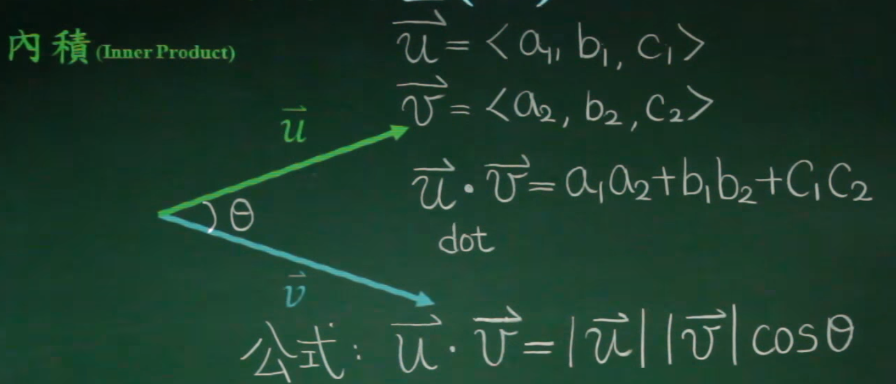


向量的应用
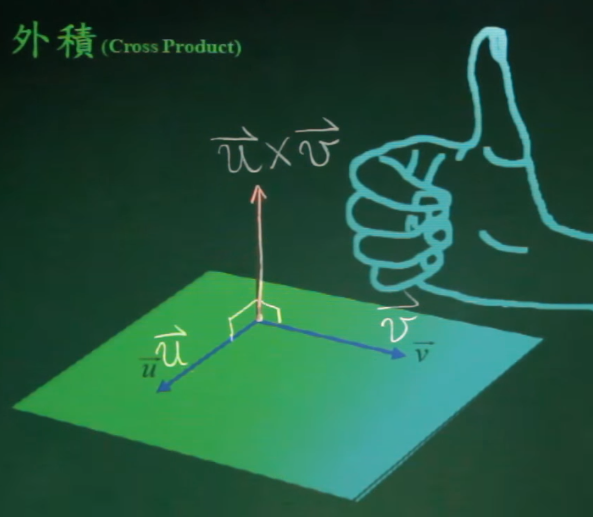
向量外积

U向量×V向量= i = (y1*z2-z1*y2), j = (z1*x2-x1*z2), k=(x1*y2-y1*x2) = <-2,1,1,>
U向量与V向量的外积是分别与U向量和V向量相垂直。
3. 平面方程式
已知点和法向量求平面方程:取平面的任一一点(x,y,z),这一点到已知点(2,-1,3)的向量,与法向量内积,便是平面方程了。
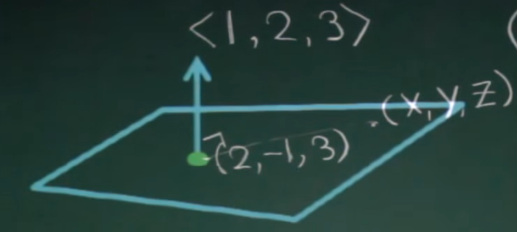
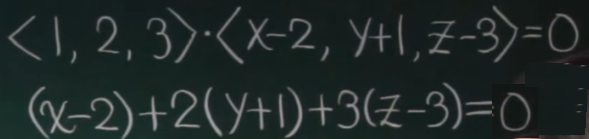
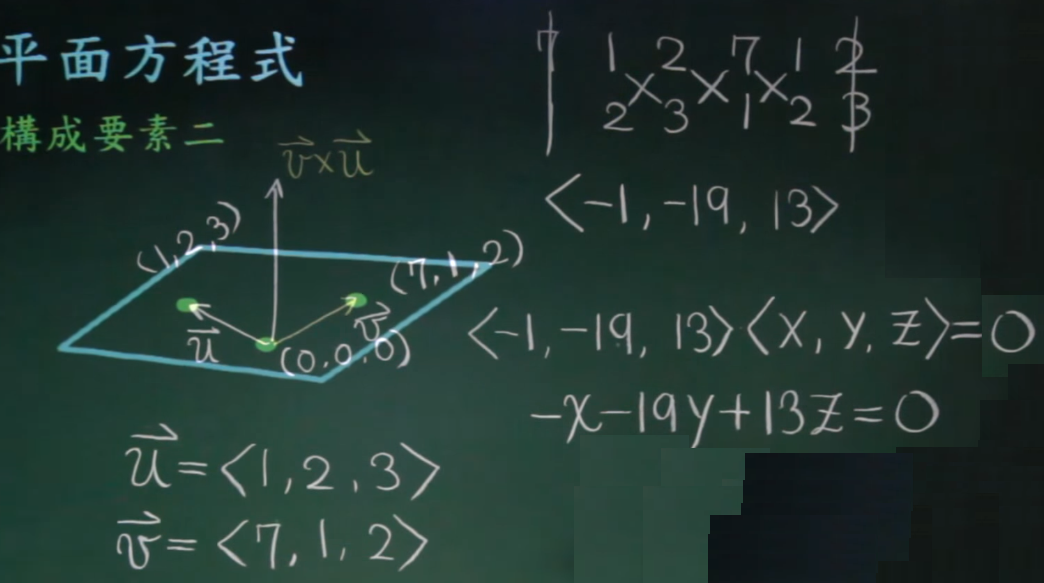
已知平面内三个点:平面的点,两两点做两个向量,平面内的两个向量的外积得到法向量,用(0,0,0)和法向量来定平面方程式。
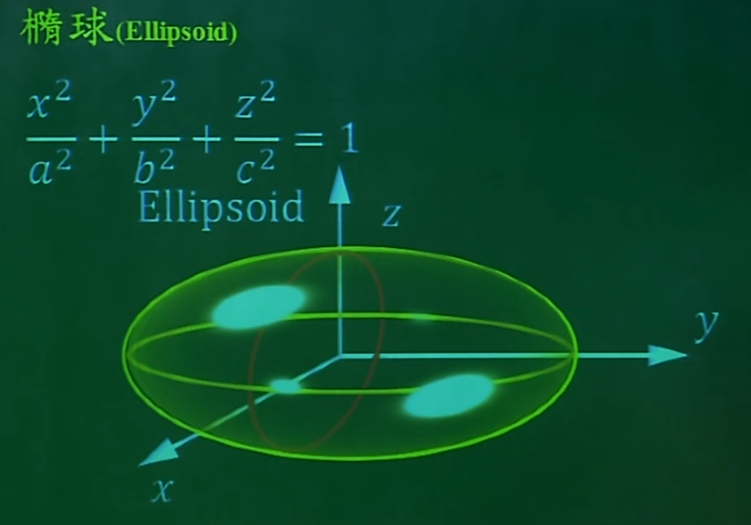
4. 二次曲线
球:x2+y2+z2=0,是以原点为中心的球。

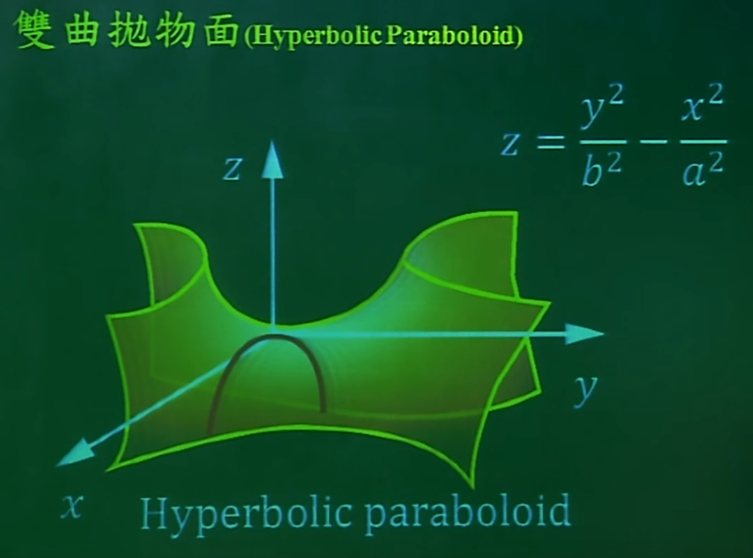
当等号右边越小,双曲面的中间部分则越向内凹。
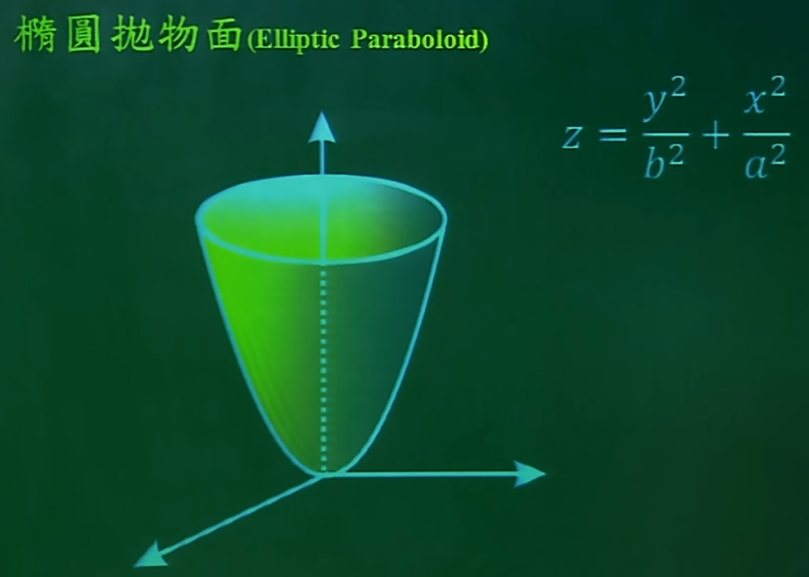
当Z为0时,为坐标系上的一个椭圆面。

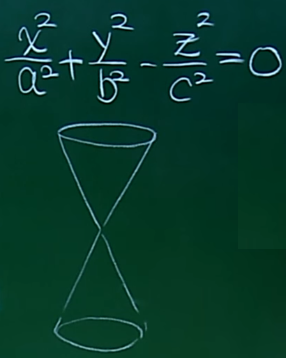
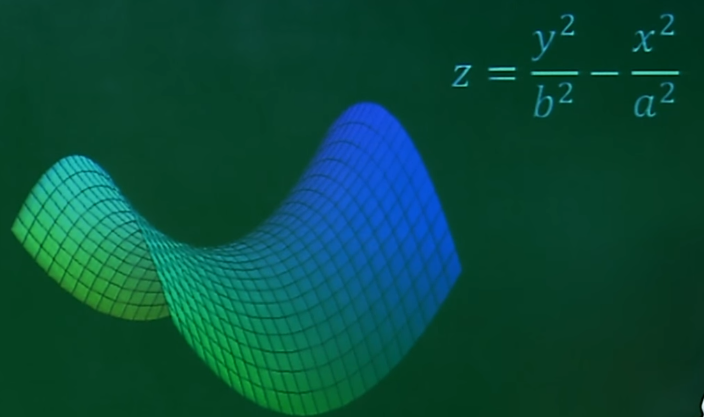
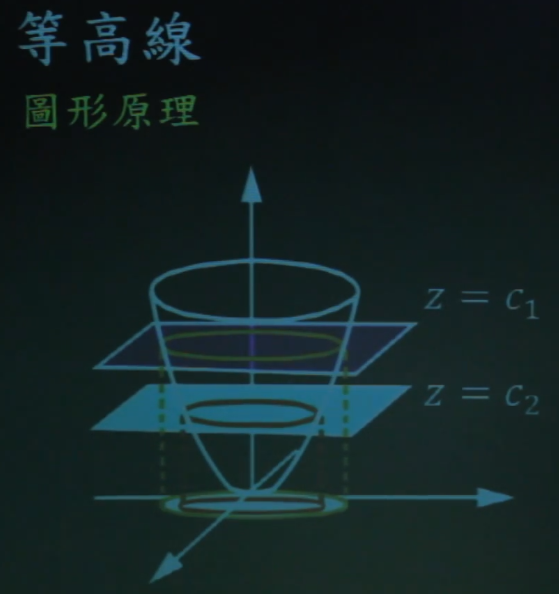
5. 等高线
等高线:在三维的空间中,怎么用二维的平面去描述。即等Z为一个常数时,Z的大小不同,相当于在不同高度对双曲线做了一个截面。 这个截面在X,Y轴上的投影所形成的截面称为等高线截面。
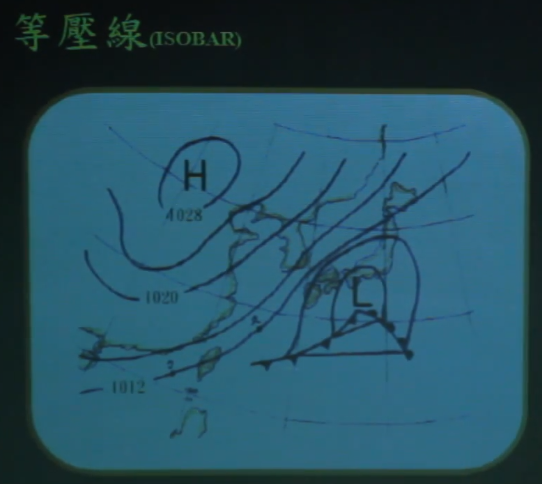
等高线的应用:等压线。
6. 偏导数
∂ 意思是partional,在多变量函数中,一个变量变动,而其他变量不变时,对多变量函数中对单变量的求导。
∂ f/∂ x:是以y不变,x为变量求导。
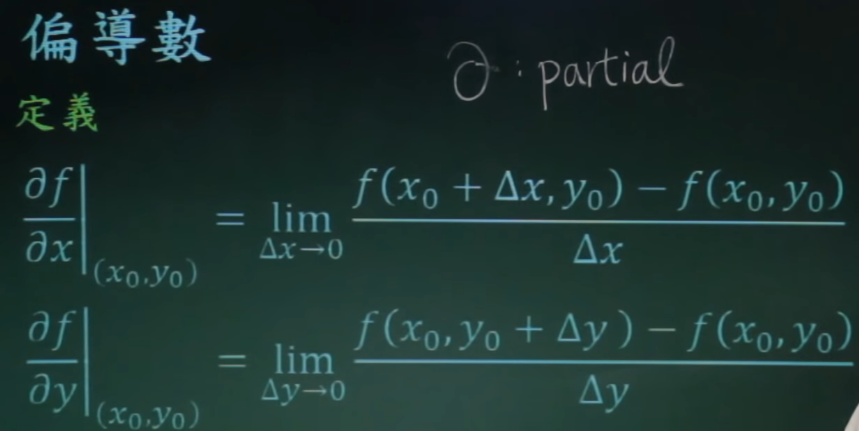
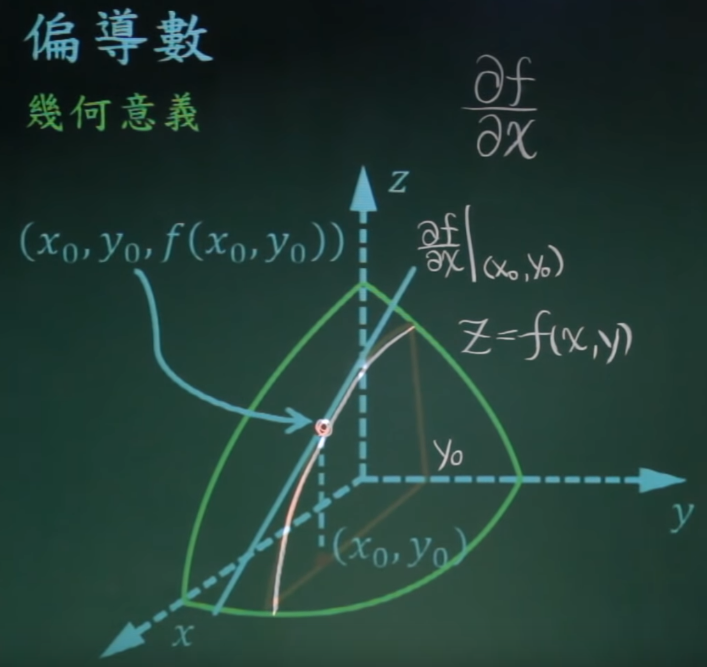
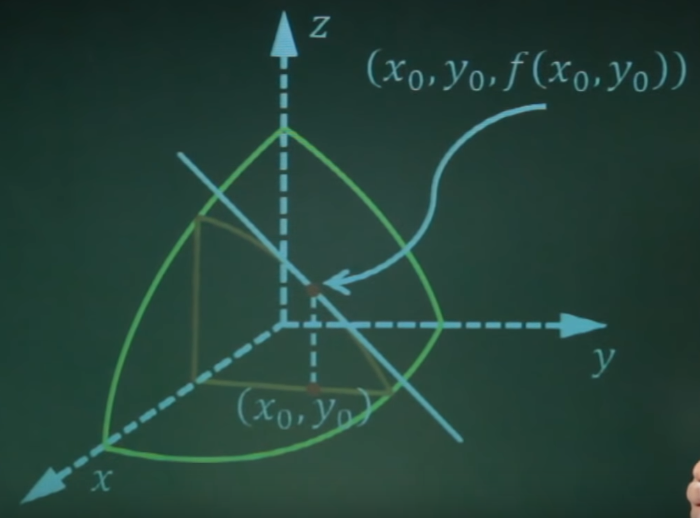
∂ f/∂ x 的几何意义:在坐标系中,y值固定,相当于是对几何图形在y0的切面,∂ f/∂ x,这是这个切面和几何图形上的切线的斜率。
同理,∂ f/∂ y 则是x0固定,对x0切面的切线斜率。
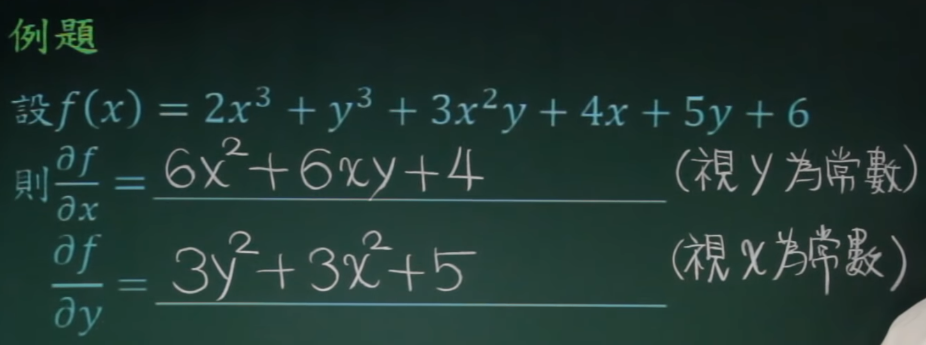
7. 函数的极限
双变量的极限,与单变量极限不同,双变量极限考察的是在空间无限靠近一条直线L。

下面的例子说明:极限不存在,由于变量x和y沿着不同的路径,得到不同的答案,则这个极限不存在。
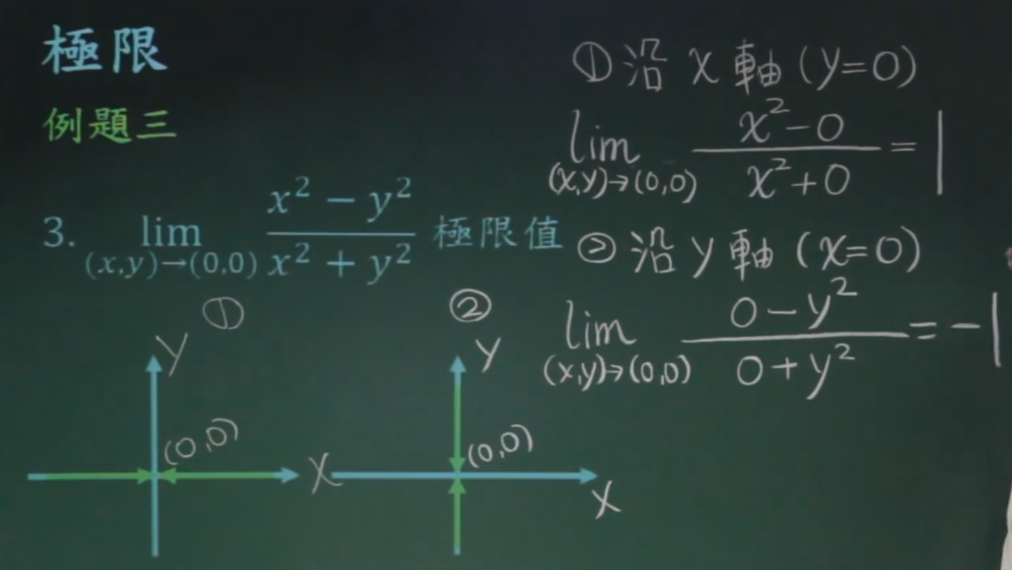
8. 双变量函数的连续性
设 f(x,y) 是一个双曲面函数,一、它在(a,b)点是存在的,二、它的极限值等于函数值。


用定义证明 f(x,y) 存在,设所有的 ξ>0, 存在 δ> 0。 即 0< |(x,y) - (0,0)| < δ => |f(x,y)-0|<ξ
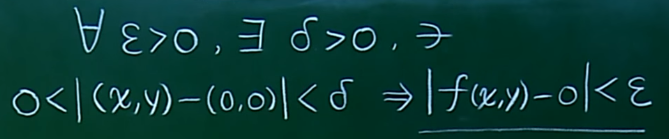
由于当(x,y) != (0,0)时,f(x,y) =|y*sin1/x| <= |y| (sin1/x <=1)。
由于 |(x,y)-(0,0)| 是一个距离sqrt(x2+y2),将f(x,y) 投影到二维空间,x,y是一个圆。距离< δ。

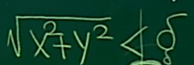
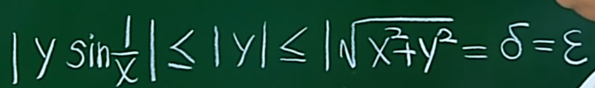
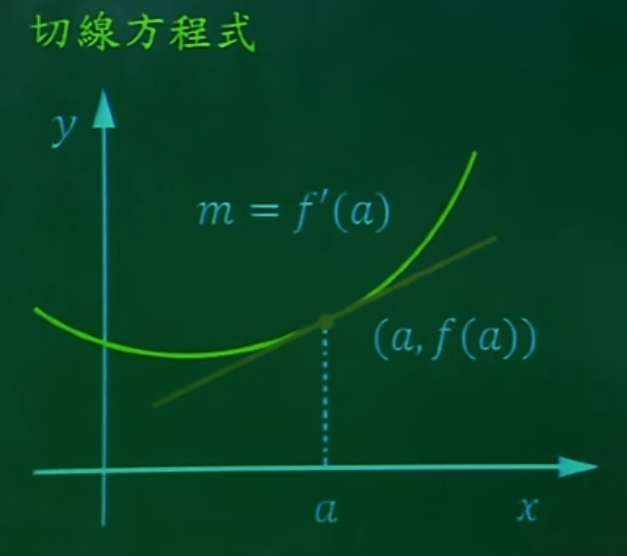
9. 切平面
切线方程式 (单变量函数)
切平面方程式:要 求法平面

求法平面,就是求当y0是常数时,a向量在x,z坐标轴的平面的切线,同理,x0是常数,b向量在y,z坐标轴平面的切线。
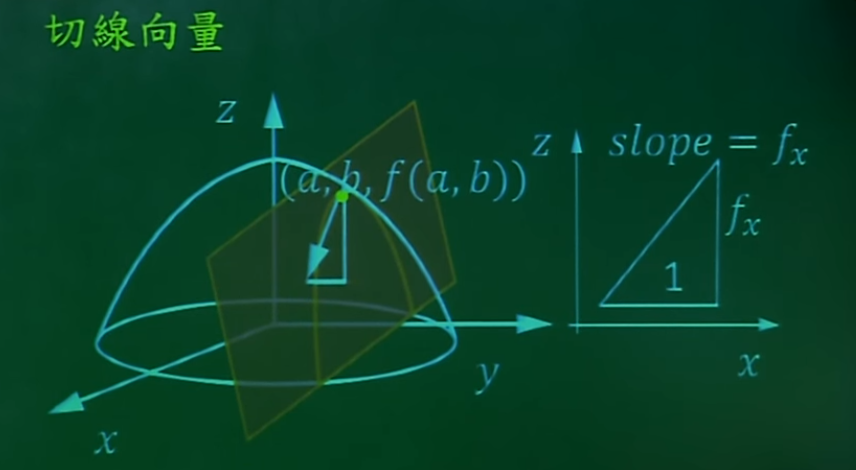
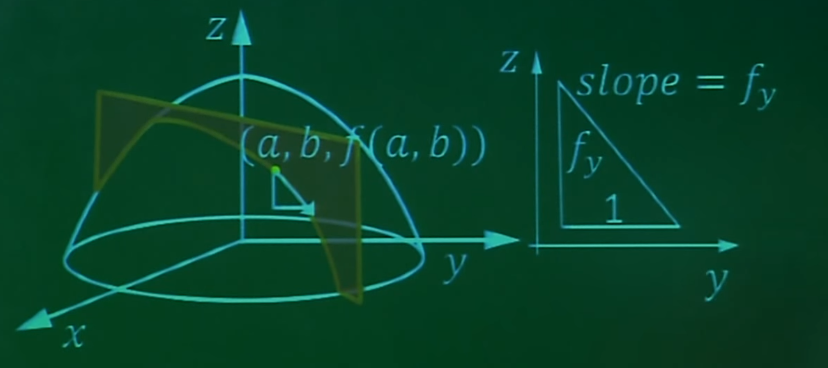
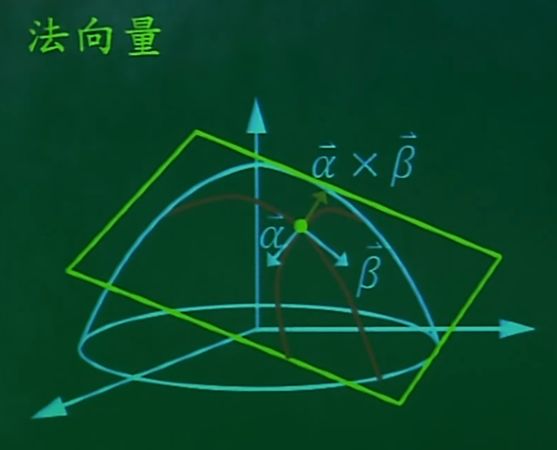
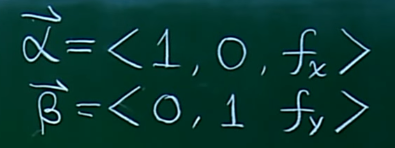
有了a向量和b向量,则可以求出函数Z=f(x,y) 的切平面的法向量为 νF=<-fx,-fy,1>。求出法向量再加上一个定点就可以求出切平面方程。
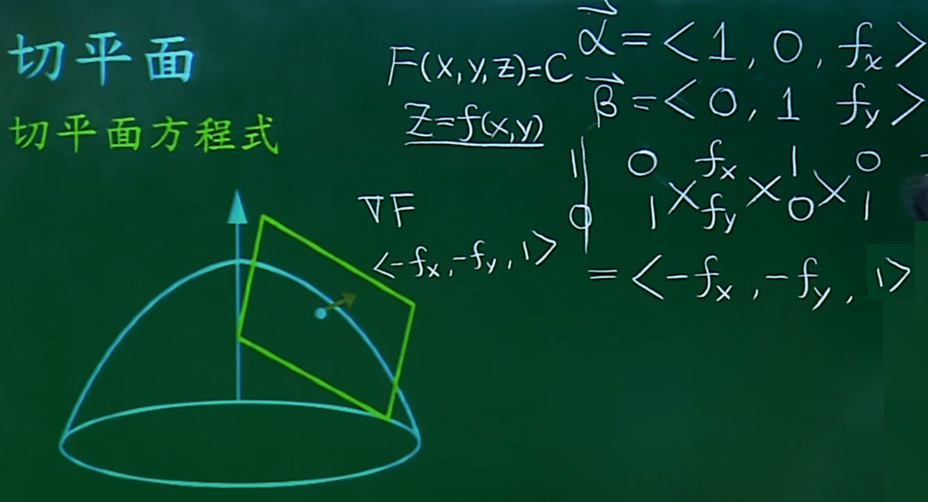
求切平面的例子

10. 高阶偏导数
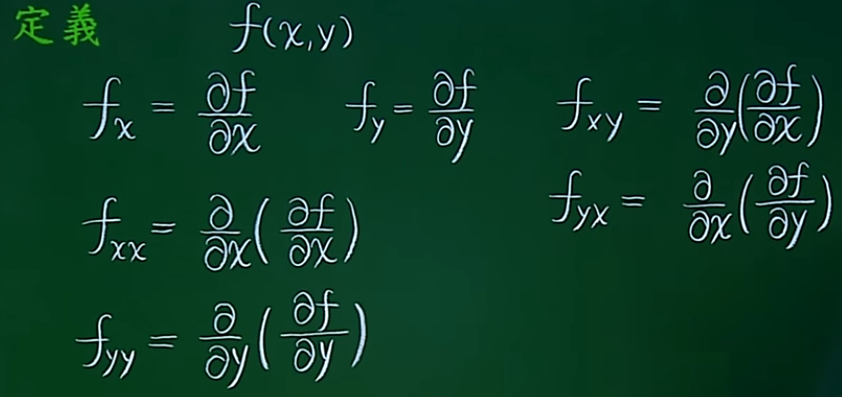
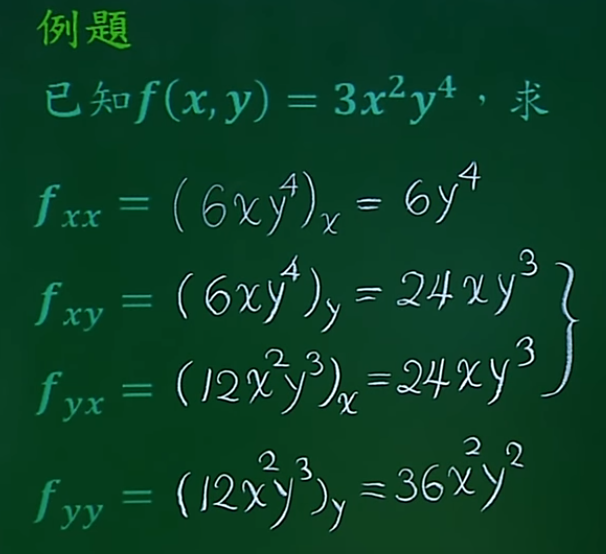
11. 全微分
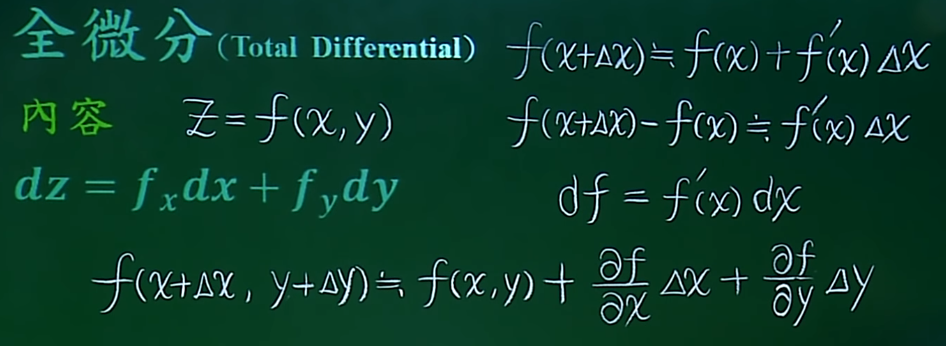
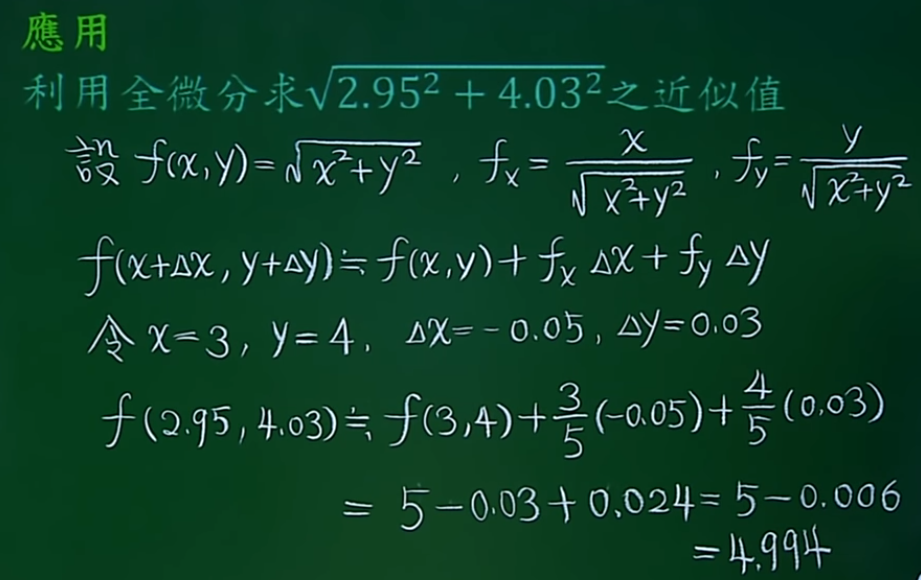
12. 相关变率

13.多元函数连锁律
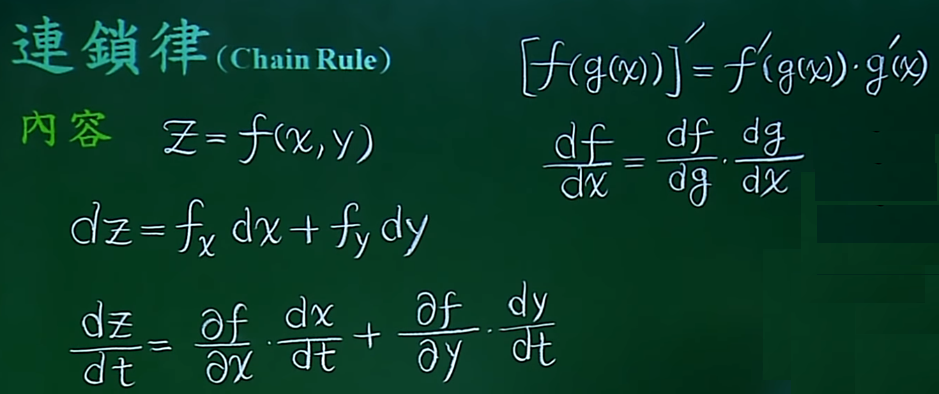
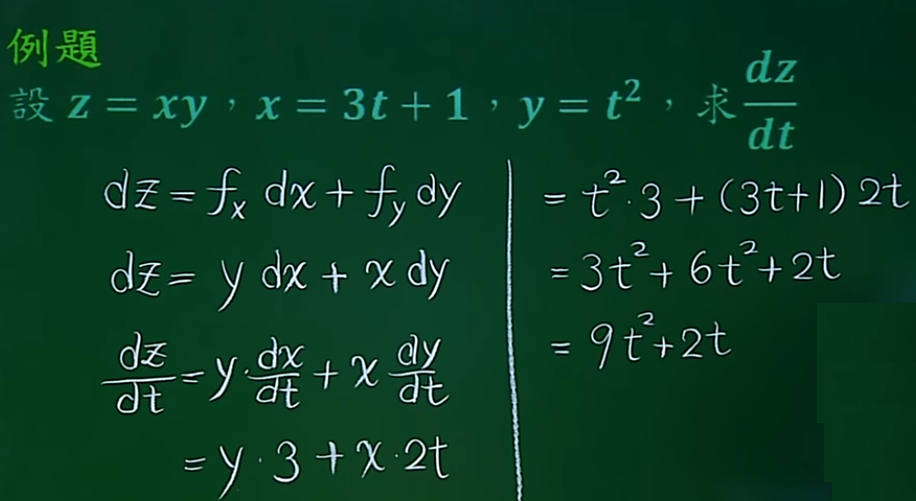



14. 隐函数的微分公式

隐函数的微分公式也可以用微分的连锁律来求,结果相同。

15. 方向导数
方向导数定义:在平面内的一个点(x0,y0),这个点对应到曲面的上这个点的方向相同的切线的斜率。

将极限的前半部分设为以h为自变量的函数f(h),对这个函数求全微分。dx/dh = u1;dy/dh=u2,所以等式Du=<Fx,Fy>*<u1,u2>
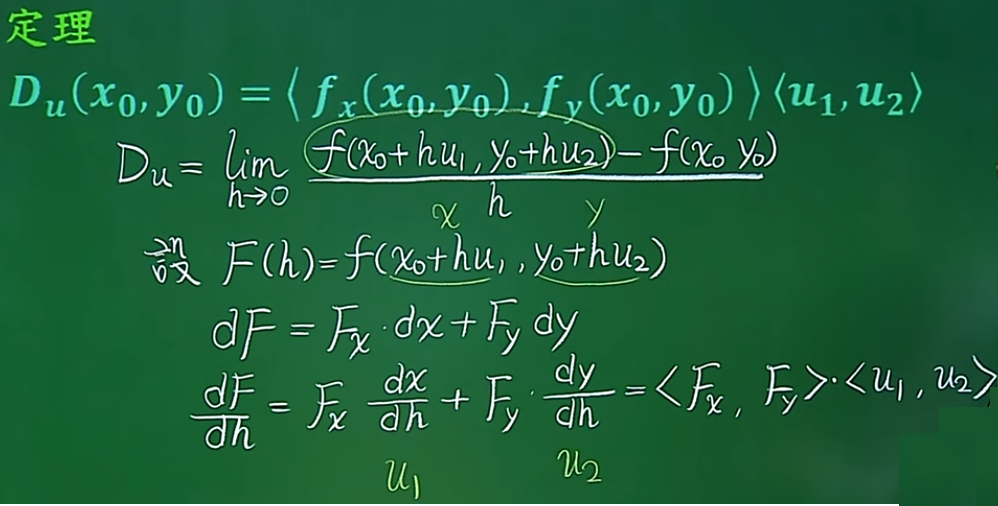
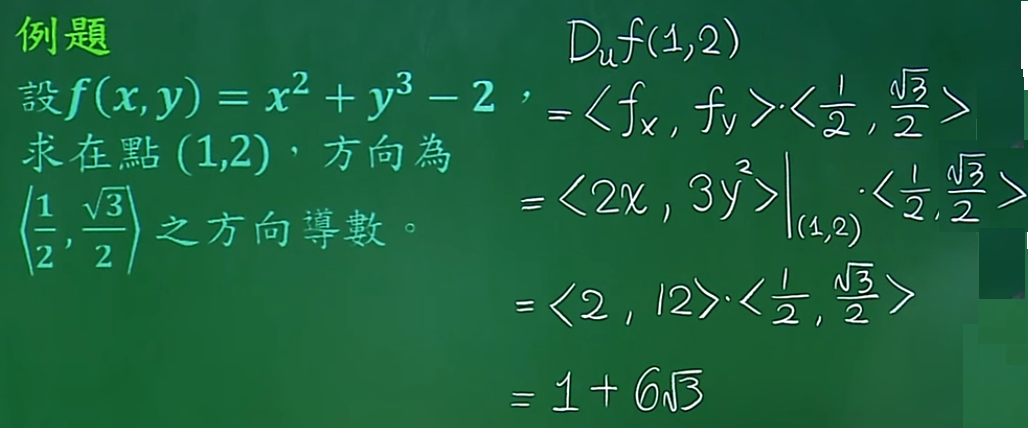
16. 梯度
梯度就是沿曲面方向的切线;而方向导数是梯度在u方向的投影,梯度方向是与在等高线上的切线垂直。
梯度νF=<fx,fy>,
方向导数 Duf = <fx,fy><u1,u2>,两个向量的点乘,即梯度在单位向量u上的投影。

极大极小值

1. 找临界值。
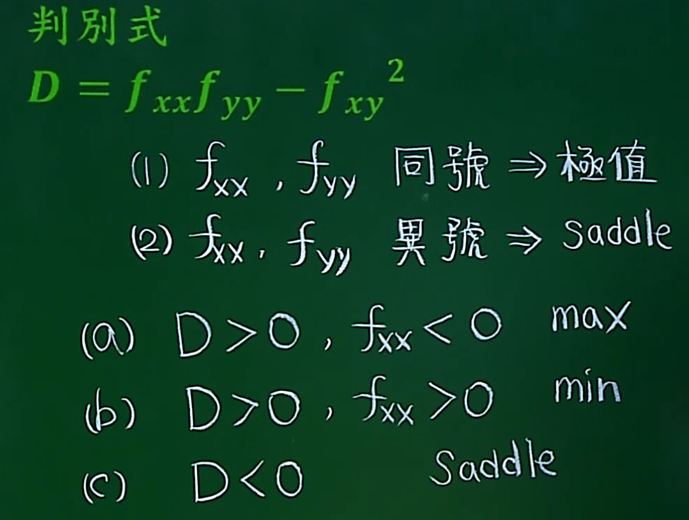
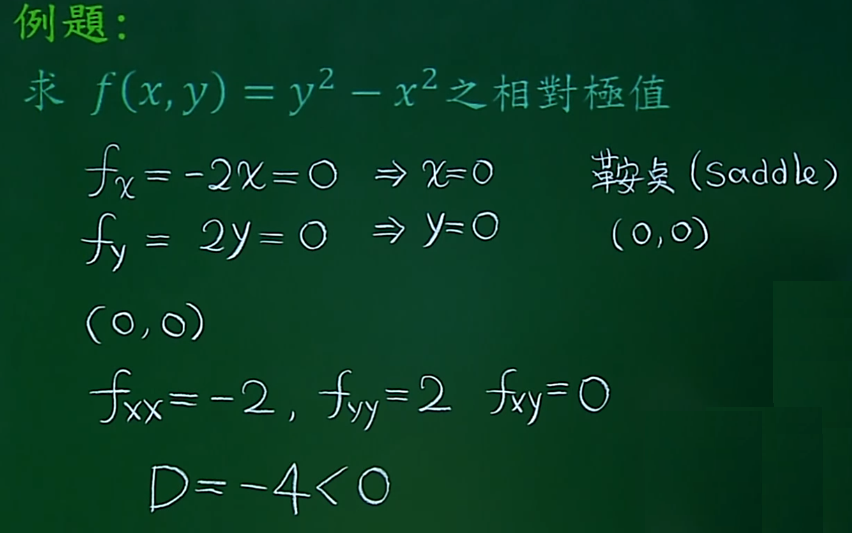
拉格朗日乘子法
三维空间的曲面,我们给他一个限制条件下,我们求他的极值。
限制条件:g(x,y)=0,这是平面上的曲线,交曲面于一个抛物线。抛物线有一个极值。将曲面投影到x,y轴上,从等高线可以看出,g(x,y)与等高线相切,相切的点就是最小值。
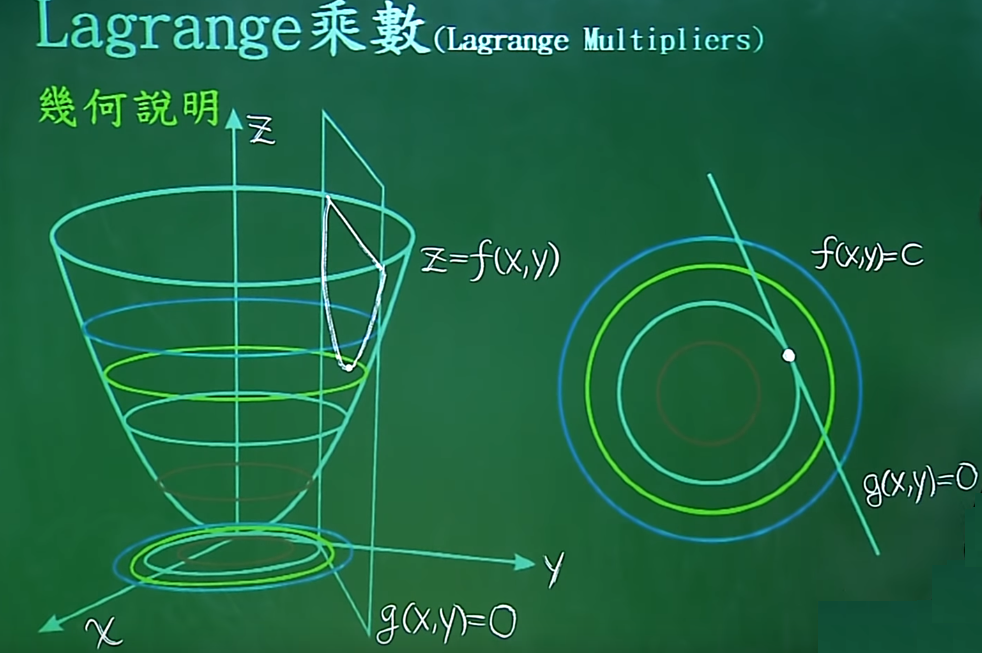
拉格朗日乘子法的几何意义,函数νf与νg是成比例的,即 νf=λνg。