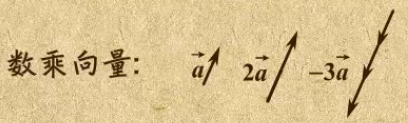空间向量
https://wenku.baidu.com/video/course/v/V_3e6e0242a8956bec0975e392
http://www.xuetangx.com/courses/course-v1:TsinghuaX+10421094X+2019_T1/about
1. 空间向量:在空间中的向量。所有的概念与平面向量相同。
- 加减法:三角形法则和平行四边形法则。
平行四边形法则:将空间的向量平移。
三角形法则:两条线相加等于起点到终点的距离
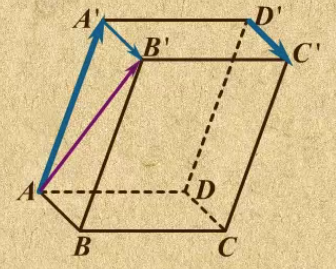
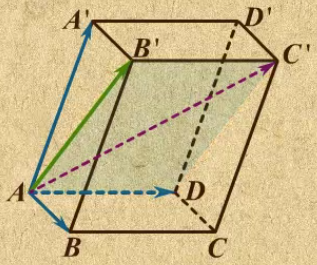
向量AA’+向量D'C' = 向量AA'+向量A'B' = 向量AB' ; 而向量AA'+向量AB+向量AD = 向量AC'
例子 重心的性质:AG=2/3AF

向量AB+向量AD+向量AP = 向量AE。
由于G是三角形ACP的重心,向量AG=2/3向量AF。向量AF为1/2AE,所以向量AG=1/3向量AE
所以1/3(AB+AD+AP)=向量AG
2. 共线与共面向量基本定理
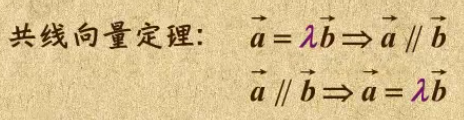
任意两个向量一定共面,因为向量是可以平移的。
而三个向量共面,必须保证他们都在一个平面上。且其中一个向量,可以被其余两个向量表示。

例子:向量是否共面,看其中一个向量是否可以被其他两个向量表示。
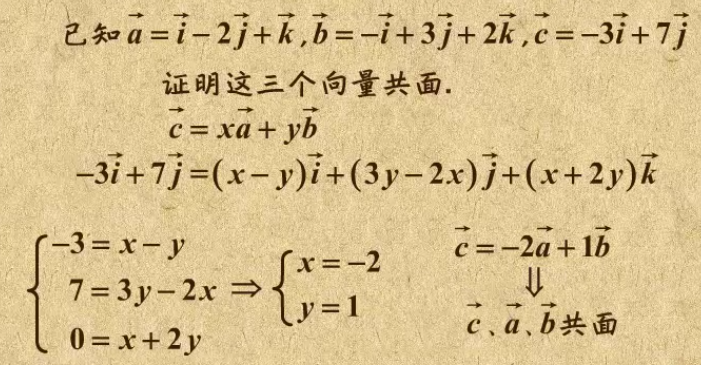
3. 空间向量分解定理
平面:平面中任意一个向量,都可以被两个不共线的向量相加。
空间:空间中任意一个向量,都可以被三个不共面的向量相加。这三个不共面的向量就是空间的基底。这就是空间向量的分解定理。
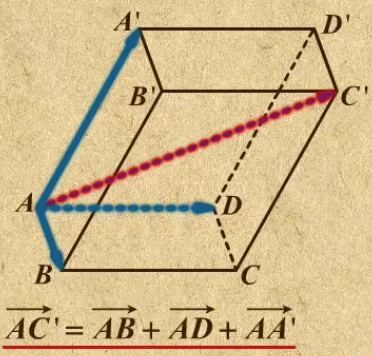

4. 空间向量数量积的直接计算
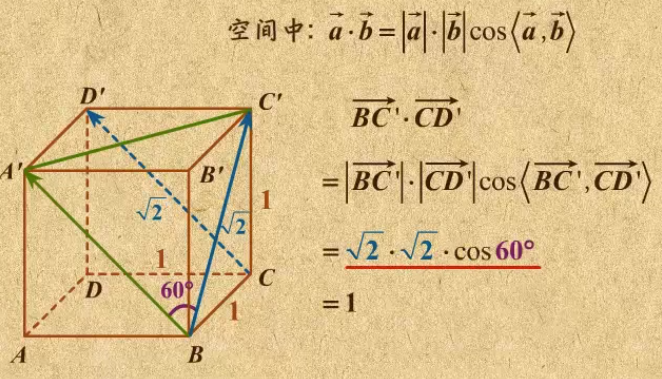
5. 空间向量的坐标混合运算
空间中的向量坐标与平面一样,都是终点减去始点。
A向量=(1,1,2);B向量=(1,3,1),AB向量=B向量-A向量=(0,2,-1)
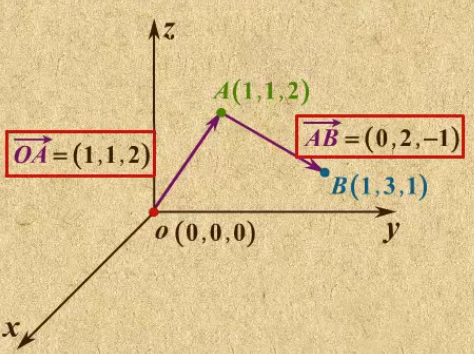
向量的运算:
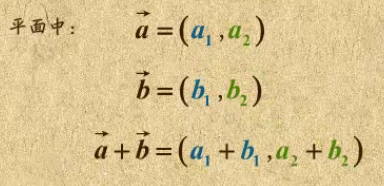
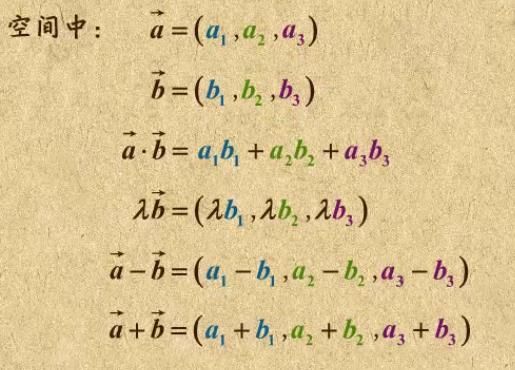
6. 向量模的计算

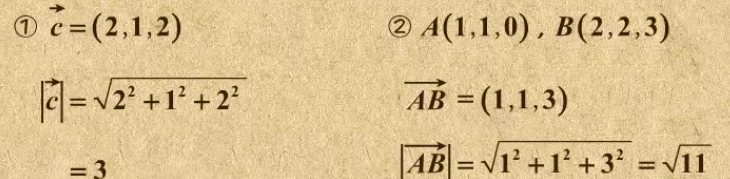
7. 空间向量平行、垂直和共面的条件
- 空间向量平行:则向量a=λ向量b。

- 空间向量垂直:则向量a*向量b=0
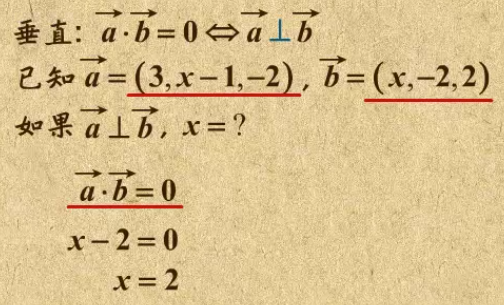
- 空间向量共面:其中一个向量能被其他两个向量线性表示

8. 向量夹角的计算
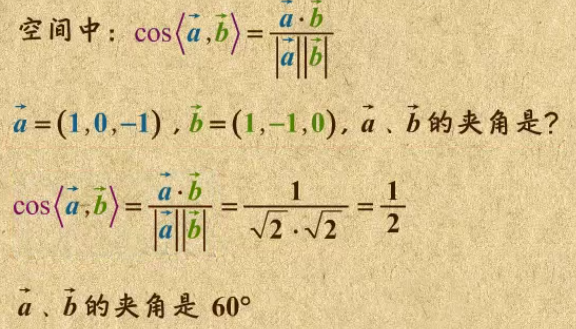
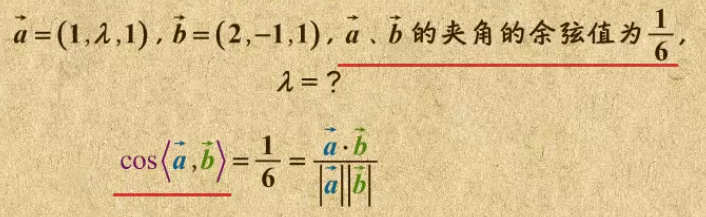
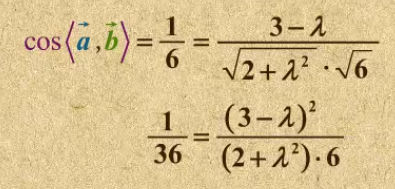
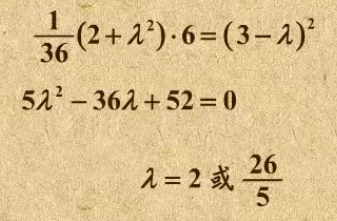
9. 向量求两条直线的夹角
计算两向量的夹角,可以建立坐标系,用转换成计算向量的坐标向量的夹角。
注:θ为正。

还可以分解计算。

10. 法向量
法向量:与平面a垂直的向量就是 平面a的法向量,但法向量并不唯一,只要是垂直于平面a的向量都是平面a的法向量。
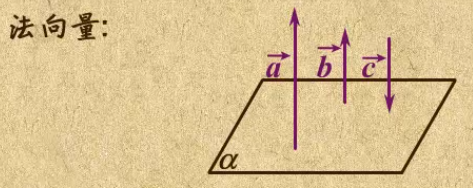
怎么查找法向量?只要在平面a内,找到两个不共线的向量垂直,那么这个向量就垂直平面
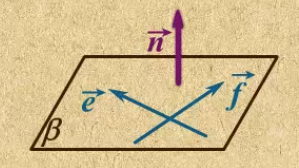
求解法向量的步骤:
- 设一个法向量
- 再利用它与平面内的不共线的向量列出公式。
- 给x取任意值。

11. 直线与平面的夹角
直线与平面的夹角为【0,∏/2】
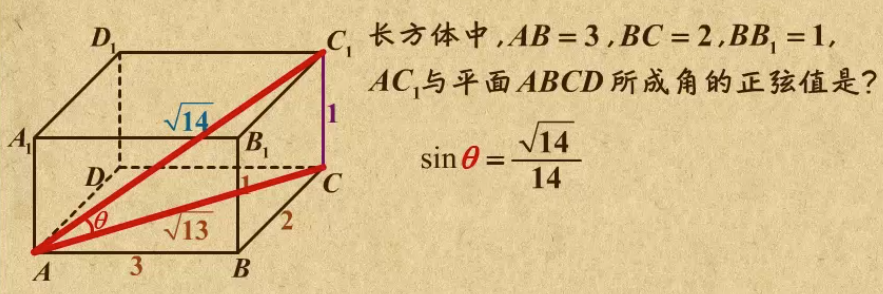
向量法:

cosθ 就是两个向量的点乘,除以两个向量的模相乘。

13. 利用向量分解求线段长
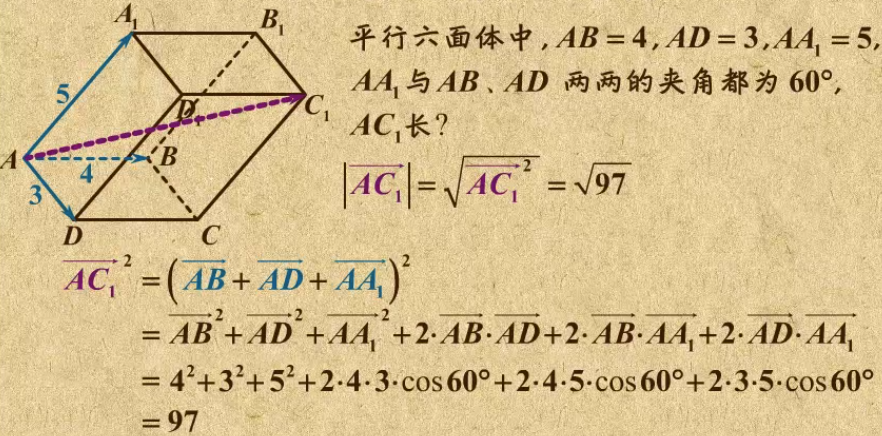
14. 点面距离
http://www.cnblogs.com/graphics/archive/2010/07/10/1774809.html
平面的一般式方程
Ax +By +Cz + D = 0
其中n = (A, B, C)是平面的法向量,D是将平面平移到坐标原点所需距离(所以D=0时,平面过原点)
向量的模(长度)
给定一个向量V(x, y, z),则|V| = sqrt(x * x + y * y + z * z)
向量的点积(内积)
给定两个向量V1(x1, y1, z1)和V2(x2, y2, z2)则他们的内积是
V1V2 = x1x2 + y1y2 + z1z2
点到平面的距离
有了上面的准备知识,则求点到直线的距离不再是难事,有图有真相

如果法相量是单位向量的话,那么分母为1
15.