前向星
在了解链式前向星之前,先简单了解下前向星。前向星是一种边集数组,先把每条边按照从小到大的顺序排序,如果起点一样,那么就按照终点从小到大来排序,并记录下每个点为起点在数组中的位置和该点所连边的数量。
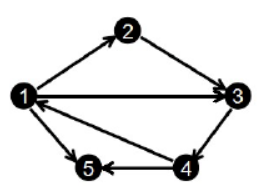
- (len[i])表示以(i)为起点的边的条数,hehiad[i]表示以(i)为起点的边在数组中存储的第一个位置
- head[1]=1,len[1]=3
- head[2]=4,len[2]=1
- head[3]=5,len[3]=1
- head[4]=6,len[4]=2
利用前向星,可以在(O(nlog_2{n}))时间内排序+处理,(O(1))时间内查询
前向星特别适合优化SPFA,DFS和BFS
链式前向星
使用结构体,添加了当前边指向的下一条边的地址,head数组存放以i为起点的边的地址,next存放下一条边的地址,当next=0时表示最后一条边。
#include<bits/stdc++.h>
using namespace std;
#define MAXN 100501
struct NODE{
int w;
int e;
int next; //next[i]表示与第i条边同起点的上一条边的储存位置
}edge[MAXN];
int cnt;
int head[MAXN];
void add(int u,int v,int w){
edge[cnt].w=w;
edge[cnt].e=v; //edge[i]表示第i条边的终点
edge[cnt].next=head[u]; //head[i]表示以i为起点的最后一条边的储存位置
head[u]=cnt++;
}
int main(){
memset(head,0,sizeof(head));
cnt=1;
int n;
cin>>n;
int a,b,c;
while(n--){
cin>>a>>b>>c;
add(a,b,c);
}
int start;
cin>>start;
for(int i=head[start];i!=0;i=edge[i].next)
cout<<start<<"->"<<edge[i].e<<" "<<edge[i].w<<endl;
return 0;
}
洛谷P1197 星球大战
基本思路
使用反并查集,使用链式前向星存储边的状况,vis表示是否被摧毁,由最后时刻反向重建,使用并查集检查联通块数目
#include<bits/stdc++.h>
#define FOR(i,a,b) for(int i=a;i<b;i++)
#define FOR2(i,a,b) for(int i=a;i<=b;i++)
#define sync ios::sync_with_stdio(false);
#define ll long long
#define INF 0x7f7f7f7f;
#define MAXN 500010
#define ok1 cout<<"OK1"<<endl
#define ok2 cout<<"OK2"<<endl
#define ok3 cout<<"OK3"<<endl
#define MOD 10007
using namespace std;
int f[MAXN],store[MAXN],ans[MAXN];
int cnt=0;bool vis[MAXN]; int h[MAXN];
typedef struct{
int w,from,to,next;
}EDGE; EDGE edges[MAXN];
void add(int u,int v)
{//链式前向星
edges[cnt].from=u;
edges[cnt].to=v;
edges[cnt].next=h[u];
h[u]=cnt++;
}
int find(int x)
{//路径压缩
if(f[x]!=x) f[x]=find(f[x]);
return f[x];
}
int main()
{
int n,m,a,b,k,x;
cin>>n>>m;
fill(h,h+MAXN,-1);
memset(vis,false,sizeof(vis));
FOR(i,0,n)
{
f[i]=i;
}
FOR(i,0,m)
{
cin>>a>>b;
add(a,b);add(b,a);//无向图
}
cin>>k;
int total=n-k;
FOR(i,0,k)
{
cin>>x;
store[i]=x;
vis[x]=true;//全部毁灭
}
FOR(i,0,2*m)
{
if(vis[edges[i].from]==false&&vis[edges[i].to]==false)
{//不是被毁灭的点
int fa=find(edges[i].from);
int fb=find(edges[i].to);
if(fa!=fb)
{
f[fa]=fb;
total--;//计算联通块,若能本来不联通,联通块数目-- ,本来联通则不变
}
}
}
ans[k]=total; //倒着重建
for(int i=k-1;i>=0;i--)
{
int u=store[i];
total++;
vis[u]=false;
for(int j=h[u];j!=-1;j=edges[j].next)
{
if(vis[edges[j].to]==false){
int fa=find(edges[j].from);
int fb=find(edges[j].to);
if(fa!=fb){
f[fa]=fb;
total--;//本来不连通,重建后联通 ,本来联通就不变
}
}
}
ans[i]=total;
}
FOR2(i,0,k)
cout<<ans[i]<<endl;
return 0;
}